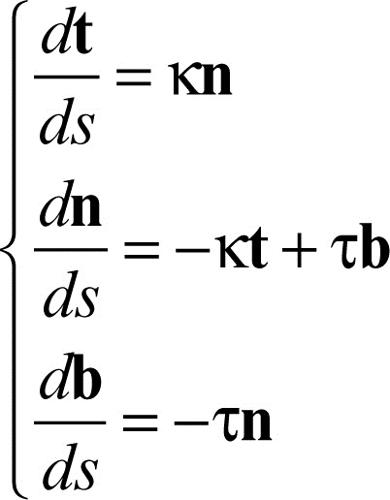Frenet, formule di
Frenet, formule di
Frenet, formule di in geometria differenziale, relazioni che legano i versori del triedro principale (t versore tangente, n versore normale, b versore binormale) relativi a un punto P di una curva dello spazio, con la curvatura ƙ = 1/R e la torsione τ in quel punto. La curva deve essere data in equazioni parametriche assumendo come parametro l’arco s e le formule di Frenet si traducono allora in relazioni fra tali equazioni e le loro derivate rispetto al parametro. Le formule di Frenet permettono di studiare le curve sghembe e di dedurne notevoli proprietà; per esempio, la costanza del rapporto tra curvatura e torsione nelle eliche cilindriche. L’espressione delle formule di Fernet è la seguente:
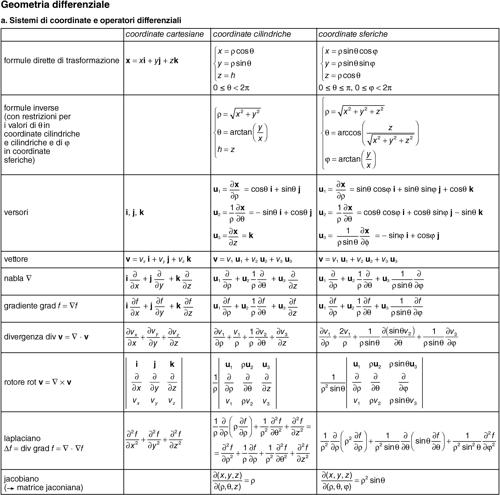
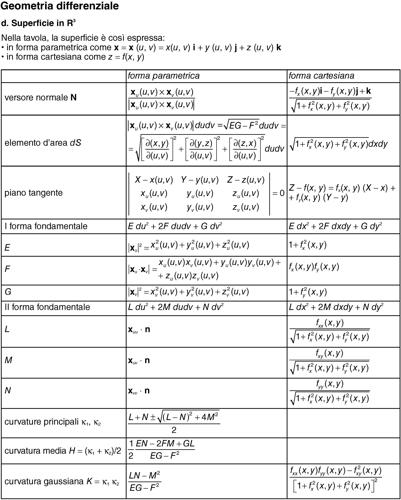
Esse esprimono, quindi, le derivate dei versori della cosiddetta terna intrinseca a una linea nello spazio rispetto alla sua ascissa curvilinea. Tali formule si possono interpretare dicendo che un osservatore solidale con la terna intrinseca, che si muove di moto uniforme lungo la linea, possiede una velocità angolare la cui componente lungo la binormale è la prima curvatura ƙ (flessione) e quella lungo la tangente è la seconda curvatura τ (torsione), mentre non esistono componenti lungo la normale principale. Si vedano le tavole delle formule di geometria differenziale.
