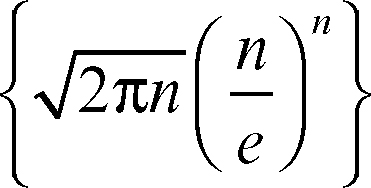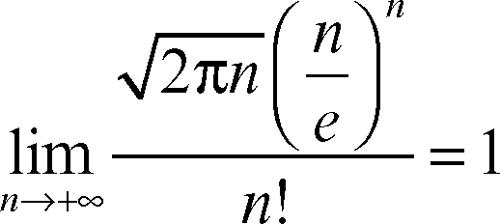Stirling, formula di
Enciclopedia della Matematica (2013)
Stirling, formula di
Stirling, formula di formula che fornisce la valutazione approssimata del → fattoriale di un numero n > 0. Essa lega la successione fattoriale alla successione
dove e è il numero di Nepero. Tali successioni hanno lo stesso andamento asintotico, vale a dire:
La formula stabilisce che
con 0 < θ < 1, e, quindi, se n è sufficientemente grande (n → +∞), allora n! è approssimabile con
Si scrive quindi
Passando ai logaritmi si ha:
La formula di Stirling è anche detta formula di Moivre-Stirling perché il primo a stabilirla, anche se con una costante diversa, fu il matematico francese A. de Moivre.