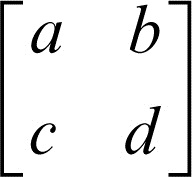forma modulare

Enciclopedia della Matematica (2017)

forma modulare


forma modulare in analisi complessa, particolare funzione olomorfa che così si definisce. Sia M2(Z) il gruppo delle matrici quadrate di ordine 2 a coefficienti interi aventi determinante uguale a 1, cioè

Enciclopedia della Matematica formula lettf 01590 001.jpg

con ad − bc = 1, e sia Γ0(n) il sottogruppo contenente le matrici che siano triangolari superiori modulo un intero positivo n. Una matrice di M2(Z) appartiene a Γ0(n) se n divide c. Dato un intero n, si fissi il gruppo Γ = Γ0(n). Una forma modulare di peso k ≥ 2 rispetto a Γ è una funzione ƒ: H → C a valori nel campo complesso, dove H è il semipiano superiore del piano di Argand-Gauss (numeri complessi con parte immaginaria positiva), che soddisfa le condizioni seguenti:

• ƒ è olomorfa su H;

• ƒ soddisfa l’equazione funzionale ƒ(γz) = (cz + d)kƒ(z) per ogni scelta di z in H e di γ in Γ dove γz indica l’elemento (az + b)/(cz + d);

• ƒ è olomorfa sull’insieme delle cuspidi. Nel caso particolare n = 1 (in tal caso il gruppo Γ coincide con M2(Z)), si richiede che sia possibile sviluppare la ƒ(z) in serie di Fourier.

Si può quindi dire che una forma modulare è una funzione olomorfa sul semipiano superiore del piano di Argand-Gauss.

Vedi anche
congruenza Nella geometria elementare, sinonimo di uguaglianza (➔) diretta, cioè di sovrapponibilità. Nella teoria dei numeri, relazione di due numeri interi relativi a, b tali che la differenza a−b è divisibile per un numero intero positivo m (detto modulo di una c.); essa si scrive a≡b (mod. m) e si legge: «a ... numeri interi In matematica, si chiamano interi positivi (o naturali) i numeri della successione infinita 1, 2, 3, 4, ... ciascuno dei quali si ottiene dal precedente aggiungendo a esso l’unità. Gli interi negativi sono numeri della successione −1, −2, −3, ... Gli interi positivi e negativi, insieme con lo zero, si ... applicazione Matematica Il concetto di a. è una generalizzazione del concetto classico di funzione (➔ corrispondenza). Si parla di a. di un insieme P in un insieme Q, quando tra i due si stabilisce una corrispondenza del tipo seguente: a ogni elemento di P corrisponde un ben determinato elemento di Q, mentre un elemento ... algebra Uno dei rami fondamentali delle scienze matematiche: in senso lato l’a. studia le operazioni, definite in un insieme, che godono di proprietà analoghe a quelle delle ordinarie operazioni dell’aritmetica. Con significato specifico è sinonimo di sistema ipercomplesso. La parola al-giabr è usata per la ...
Tag
Altri risultati per forma modulare
  • forme modulari
    Enciclopedia della Scienza e della Tecnica (2008)
    Massimo Bertolini Si indichi con SL2(ℤ) il gruppo delle matrici 2×2 a coeffcienti nell’anello ℤ degli interi relativi aventi determinante 1, e con Γ0(N) il sottogruppo contenente le matrici che sono triangolari superiori modulo un intero positivo N. Gli elementi di SL2(ℤ) sono le matrici [1] con ...
Vocabolario
mòdulo
modulo mòdulo s. m. [dal lat. modŭlus, dim. di modus «misura»]. – In genere, misura, forma, esemplare, che si assume come modello a cui attenersi, o come elemento fondamentale secondo il quale determinare o proporzionare le misure di un...
modulare¹
modulare1 modulare1 agg. [der. di modulo]. – Relativo a un modulo (nel suo sign. primo e più generale), basato su un modulo, e quindi anche costituito dal vario accostamento di elementi (detti essi stessi elementi m.) che ripetono le misure,...