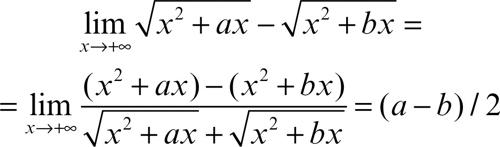forma indeterminata

forma indeterminata

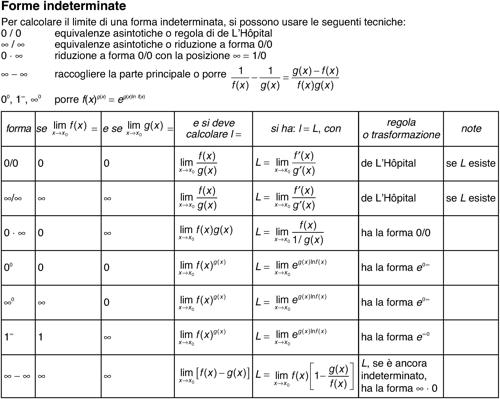
forma indeterminata espressione ottenuta come risultato di una operazione tra due funzioni o della loro composizione, il cui limite non può essere stabilito a priori dalla conoscenza separata dei limiti delle funzioni stesse. Le forme indeterminate sono sette, e precisamente: 0/0, ∞/∞, 0 ⋅ ∞, 0⁰, ∞⁰, 1^∞, ∞ − ∞ (si veda la tavola delle forme indeterminate).

Per esempio, dire che 0/0 è una forma indeterminata significa dire che se ƒ e g sono due funzioni che ammettono limite 0, il quoziente ƒ(x)/g(x) può ammettere limite finito o infinito, o non avere limite, a seconda dei casi. Per x → 0⁺, per esempio, scegliendo ƒ(x) = λx^α (λ ≠ 0), g(x) = x^β, con α, β > 0: il quoziente ƒ(x)/g(x) = λx^α−β tende rispettivamente a 0, λ o ∞ a seconda che sia α > β, α = β, α < β. Per x → +∞ lo stesso rapporto ha la forma ∞/∞, e tende rispettivamente, nei tre casi, a ∞, λ, 0. Sempre per x → ∞, il rapporto tra gli infiniti ƒ(x) = x(2 + cosx) e g(x) = x non ammette limite. Analoghi esempi mostrano che anche le altre forme possono dare qualunque limite, finito o infinito, o non ammettere limite.

La risoluzione delle prime tre forme indeterminate (0/0, ∞/∞, 0 ⋅ ∞) si può ottenere mediante opportune equivalenze asintotiche, anche se nei casi più semplici si può ricorrere alla regola o teorema di → L’Hôpital, usando eventualmente la trasformazione 1/0 = ∞. I secondi tre casi si riducono al caso 0 ⋅ ∞ mediante l’identità ƒ(x)^g(x) = e^{g(x) ln f(x)}.

L’ultimo caso è genuinamente indeterminato solo se il rapporto ƒ(x)/g(x) → 1 o non ammette limite. Infatti, se, per esempio,

si ha

e non si ha indeterminazione. Esso si può trattare, nei casi più semplici, mediante prodotti notevoli. Per esempio:

Alternativamente, dovendo per esempio calcolare

invece di usare la formula di decomposizione della differenza p⁶ − q⁶ si raccoglierà x da entrambi i radicali, ottenendo la forma indeterminata

del tipo ∞ ⋅ 0; quindi si utilizzerà due volte lo sviluppo binomiale (1 + t)^α = 1 + αt + o(t) con t = a /x e α = 1/2 nel primo, t = b /x e α = 1/3 nel secondo, per ottenere che il termine ƒ(x) tra parentesi ha l’andamento asintotico

per x → 0, da cui il limite a /2 − b /3. E, se necessario, si utilizzeranno più termini dello sviluppo: per esempio, per il caso completo in cui si voglia determinare, al variare dei parametri, l’ordine di infinitesimo di

si scriverà la funzione come

e si procederà in modo analogo con t = a /x + a′Ix ² nel primo (e analogamente per il secondo radicale), aggiungendo allo sviluppo binomiale i termini che man mano servono:

avendo l’avvertenza di far comparire simultaneamente tutte le potenze negative di x aventi lo stesso esponente. Analogamente per studiare l’andamento per x → 0 di g(x) = cotx − 1/x si scriverà

e, posti a numeratore

e a denominatore, in assenza di termini che si cancellano, semplicemente sinx = x, si otterrà g(x) ~ − x/3. Con la regola di de L’Hôpital si sarebbe ottenuto, con due derivazioni, che il limite è zero, ma per ottenere la valutazione si sarebbe dovuto dividere per x e derivare di nuovo tre volte.