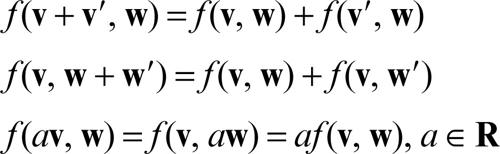forma bilineare

forma bilineare

forma bilineare in algebra lineare, applicazione ƒ che a ogni coppia di vettori v e w, rispettivamente appartenenti agli spazi vettoriali reali V e W, associa un numero reale, dotata della proprietà di linearità rispetto a v per ogni fissato w e rispetto a w per ogni fissato v:

Se V = W e gli spazi hanno dimensione finita, allora, fissata una base {e₁, ..., e_n} di V e indicati rispettivamente con x e y i vettori delle coordinate di due vettori v e w rispetto a tale base, una forma bilineare ƒ è rappresentabile sotto forma di matrice: se A è la matrice quadrata a coefficienti in R definita da A = (ƒ(e_i, e_j)_ij), allora ƒ(v, w) = v^T Aw, dove v^T è il vettore riga trasposto di v e dove il prodotto è quello righe per colonne. Due matrici A e B quadrate di ordine n a coefficienti in K esprimono la stessa forma bilineare rispetto a due diverse basi se e solo se esse sono congruenti (→ matrici, congruenza di).

Una forma bilineare ƒ si dice degenere se esiste un vettore v tale che ƒ(v, w) = 0, per ogni vettore w; in caso contrario ƒ è detta non degenere: ƒ è non degenere se e solo se la matrice associata è invertibile.

Una forma bilineare ƒ si dice simmetrica se

per ogni coppia di vettori v, w; antisimmetrica se ƒ(v, w) = −ƒ(w, v) per ogni coppia di vettori v, w; alternante se ƒ(v, v) = 0 per ogni vettore v. Ogni forma alternante è in particolare una forma antisimmetrica. Mentre la matrice associata (rispetto a una qualsiasi base) a una forma bilineare simmetrica è simmetrica, quella associata a una forma bilineare antisimmetrica è antisimmetrica. Le forme bilineari simmetriche sono particolarmente importanti in quanto a partire da esse possono essere definite le forme quadratiche e oggetti di natura metrica come i prodotti scalari. Il prodotto scalare è infatti una forma bilineare simmetrica definita positiva (ossia tale che ƒ(v, v) > 0 per ogni v ≠ 0).

Si definisce in modo analogo la nozione di forma multilineare, quale forma che gode della proprietà di linearità rispetto a ciascuno dei vettori della n-pla (v₁, ..., v_n). Un esempio di forma multilineare alternante è dato dal determinante di una matrice quadrata, pensato come funzione delle colonne della matrice.