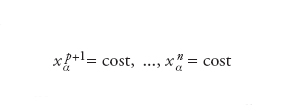foliazione

di Luca Tomassini - Enciclopedia della Scienza e della Tecnica (2008)

foliazione

Luca Tomassini

Decomposizione di un oggetto geometrico n-dimensionale (una varietà) in termini di altri oggetti (sottovarietà) di dimensione più bassa, detti foglie. Più precisamente, si richiede l’esistenza di un ricoprimento di M{[ in termini di insiemi aperti Uα sui quali siano definite coordinate locali x1α,...,x{[α:Uα⊂M{[→ℝ{[ in termini delle quali le foglie locali (le componenti connesse delle intersezioni tra le foglie e gli Uα) siano date dalle equazioni

formula

Imponendo condizioni di regolarità (continuità, differenziabilità, analiticità) alla varietà M{[ e alle coordinate locali sopra introdotte si ottengono foliazioni regolari (continue, differenziabili, analitiche). L’intero p è detto dimensione della foliazione, n−p codimensione. Per componenti connesse di un insieme si intendono qui sottoinsiemi tali che qualunque coppia di punti possa essere congiunta da una curva continua tutta contenuta in essi. La definizione sopra fornita dipende dagli intorni Uα ed è dunque di natura locale. Il passaggio da proprietà locali a proprietà globali è stato fin dall’inizio uno dei principali problemi della teoria delle foliazioni. D’altro canto, la creazione della stessa nozione di foliazione fu in parte stimolata dagli sviluppi della teoria dei sistemi dinamici, nel qual caso la varietà M{[ è lo spazio delle fasi e la sua decomposizione in traiettorie distinte è una foliazione (con l’eccezione dei punti di equilibrio). Un ulteriore esempio di foliazione è fornito dalla decomposizione di un gruppo di Lie in classi laterali rispetto a un sottogruppo analitico. Infine, nel campo dei numeri complessi, le soluzioni di un’equazione differenziale dw/dz=f(z,w) con membro a destra analitico formano (se viste come coppie di soluzioni reali) una foliazione bidimensionale.

→ Geometria non commutativa

Vedi anche
foliazione In topologia, nozione, introdotta da C. Ehresmann e G. Reeb verso il 1950, che generalizza quella di spazio fibrato e che ha originato un ramo della topologia differenziale oggetto di ricerche e studi approfonditi. Sia Vn una varietà differenziabile di dimensione n e sia data un’applicazione differenziabile ... traiettoria In fisica, con riferimento a un punto in moto, la linea, retta o curva, descritta dal punto nel suo movimento. La t. di un punto ha, come ogni elemento cinematico, carattere relativo, varia cioè in generale al variare dell’ente al quale il moto viene riferito. Se l’ente di riferimento è individuato mediante ... proprietà commutativa In matematica, si dice che un’operazione binaria gode della proprietà c. se è tale che a R b=b R a, dove R è il simbolo dell’operazione e a, b gli elementi su cui si opera. Tale proprietà c. vale, per es., per l’addizione e per il prodotto ordinario: se a e b sono numeri reali (in partic., frazioni o ... ricoprimento matematica Nella teoria degli insiemi, dato un insieme A, si dice che una famiglia {Ta} di suoi sottoinsiemi costituisce un r. di A, se l’unione degli insiemi Ta dà l’insieme A, cioè se ogni elemento di A appartiene a qualche Ta. Si parla di r. finito, infinito, numerabile ecc. a seconda che tale sia ...
Categorie
Tag
Vocabolario
foliazióne
foliazione foliazióne (o fogliazióne) s. f. [der. di foglio (o del lat. folium)]. – 1. In codicologia e bibliologia, la numerazione dei fogli di un codice o di un libro a stampa (nel primo caso è sinon. di cartolazione per gli studiosi...