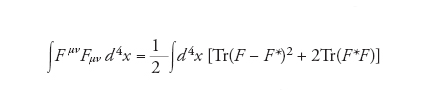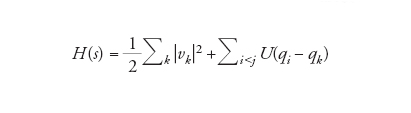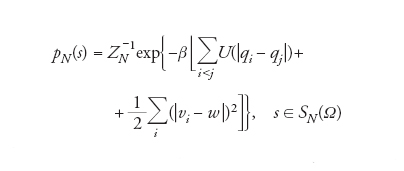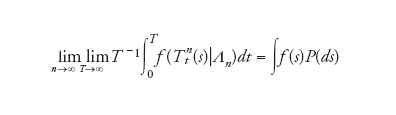Fisica matematica
Fisica matematica
La fisica matematica si può definire come la disciplina scientifica che si propone di descrivere in termini matematici rigorosi i fenomeni fisici. La ricerca in fisica matematica si articola in tre fasi, che caratterizzano questa disciplina e la distinguono da altre branche della fisica e della matematica. Nella prima fase si procede alla costruzione di un modello che riesca a rappresentare gli aspetti che si considerano importanti nel fenomeno fisico in esame. Un modello è quindi una struttura, descritta in termini matematici, il cui scopo è di far corrispondere enti del linguaggio matematico alle componenti di un fenomeno fisico e alle loro relazioni. Per esempio, un modello del sistema Terra-Luna può essere costituito da due punti geometrici nello spazio tridimensionale, ai quali siano associati due parametri (le masse dei relativi corpi celesti) e la forza con cui si attraggono. Il modello non è una rappresentazione fedele della realtà, per esempio nel caso in esame non sono prese in considerazione l'estensione e la composizione dei corpi celesti, ma ne fornisce una prima approssimazione. Modelli più raffinati si possono considerare successivamente, per esempio trattando Terra e Luna come solidi geometrici a densità variabile.
Nella costruzione di un modello si parte in generale da strutture semplici, per modificarle successivamente, ricercando un compromesso tra la difficoltà dei problemi matematici posti dal modello e l'accuratezza con cui questo rappresenta il sistema fisico. Per definizione nessun modello descrive tutti gli aspetti della realtà, e il fisico matematico deve saper cogliere le componenti significative nel fenomeno che vuole analizzare. La seconda fase della ricerca consiste nel 'risolvere' il modello che si è costruito. Poiché questo (piuttosto che la realtà) è trattato in termini matematici, utilizzando strutture che possono essere anche molto diverse tra loro, la soluzione del modello può di volta in volta significare cose abbastanza diverse. Di solito i modelli meccanici, relativi per esempio al Sistema solare, alla meccanica dei fluidi, alla deformazione dei corpi elastici o al comportamento di corpi dotati di carica elettrica in un campo elettromagnetico, comprendono due componenti principali: i possibili stati del sistema e l'equazione di evoluzione. In questo caso, risolvere il modello significa dimostrare che, in corrispondenza di ciascun dato iniziale, esiste una e una sola soluzione dell'equazione di evoluzione ed eventualmente descrivere, almeno qualitativamente, le sue proprietà. In altri modelli, quali quelli che si adottano in meccanica statistica o nella descrizione dell'equilibrio dei corpi elastici, per ottenere la soluzione si cerca di individuare una configurazione, non necessariamente unica, che minimizzi una quantità che si considera empiricamente rilevante, per esempio l'energia, l'entropia o l'energia di superficie. In questa seconda fase, il fisico matematico utilizza strumenti di varia natura, appartenenti a campi diversi della matematica: analisi, algebra, geometria, analisi numerica, calcolo delle probabilità, ecc.; in molte occasioni si trova a dover modificare o perfezionare tali strumenti e talvolta a costruirne di nuovi, più adatti allo studio del problema specifico. La fase finale della ricerca in fisica matematica consiste nell'utilizzare i risultati matematici ottenuti per dedurre stime e previsioni sul comportamento del sistema fisico in esame.
Questa suddivisione in tre fasi è comune anche ad altre discipline che si propongono di descrivere fenomeni fisici, ma in campi di ricerca diversi dalla fisica matematica la struttura matematica logico-deduttiva della seconda fase lascia spesso il posto a considerazioni almeno in parte euristiche e congetturali. È peraltro vero che anche nell'attività di un fisico matematico queste previsioni certe, sotto forma di teoremi, sono in generale precedute da una fase in cui giocano un ruolo determinante l'intuizione, l'analisi di modelli elementari, le analogie e i calcoli preliminari (in questo, in tempi recenti hanno avuto un ruolo di primo piano i calcolatori elettronici). Solamente in un secondo momento, alla luce delle considerazioni qualitative fatte, sono enunciati e dimostrati teoremi.
Descriverò qui alcuni temi di ricerca in fisica matematica nei loro sviluppi recenti. Ho cercato di rendere l'esposizione accessibile a un publico di non specialisti; in alcuni punti tuttavia la presentazione ha necessariamente carattere più tecnico. Si vede da questi esempi che la ricerca in fisica matematica presenta attualmente un notevole grado di differenziazione e di specializzazione sia per quanto riguarda le problematiche che le tecniche matematiche utilizzate.
Dall'elettromagnetismo alla teoria di Yang-Mills
Uno dei più notevoli sviluppi della fisica matematica nel XX sec. riguarda la teoria di gauge, dal punto di vista sia classico sia quantistico. Iniziamo ricordando brevemente la struttura delle equazioni di Maxwell; utilizzeremo il formalismo covariante per sottolineare il fatto che queste equazioni sono covarianti per trasformazioni di Lorentz. Indichiamo con xμ, μ=0,1,2,3, le coordinate spazio-temporali in un riferimento inerziale, con x0=ct, dove c è la velocità della luce nel vuoto. Le trasformazioni di Lorentz sono date da x′μ=Lμνxν, dove si sottintende la somma su indici ripetuti e dove le matrici L soddisfano la relazione LtgL=g, essendo g la metrica di Lorentz (Lt è la matrice trasposta di L). Indichiamo con Fμν(x) il tensore antisimmetrico che caratterizza il campo elettromagnetico. Le relazioni tra la matrice antisimmetrica F e i campi vettoriali elettrico E e magnetico B sono espresse (in opportune unità di misura) da Ek(x)=F0k(x) e Bk(x)=(1/2)εklmFlm(x), k,l,m=1,2,3, dove ε è il simbolo totalmente antisimmetrico. Indichiamo con ∂μ l'operazione di derivata parziale rispetto alla coordinata xμ, dove xμ=gμνxν. Con queste notazioni le equazioni di Maxwell si scrivono nel modo seguente:
[1] ∂μFμν(x) = jν(x), ∑ciclica∂μFμν(x) = 0
dove j rappresenta il quadrivettore carica-corrente elettrica.
In particolare, la [1] garantisce che ciascuna componente del campo elettromagnetico nel vuoto soddisfi le equazioni delle onde (le equazioni di Maxwell sono un sistema iperbolico, descrivono cioè una propagazione a partire da dati iniziali) e rappresenti quindi un'onda che si propaga (nel vuoto) con velocità che non dipende dalla velocità della sorgente rispetto al ricevitore. La prima delle equazioni di Maxwell [1] descrive l'interazione, la seconda è puramente geometrica e indica che il campo di matrici antisimmetriche F può essere scritto, almeno localmente, nella forma Fμν(x)=∂μAν(x)−∂νAμ(x) per un campo vettoriale A (potenziale elettromagnetico). Il campo A(x) è definito da questa relazione soltanto a meno di una trasformazione Aμ(x)→Aμ(x)+∂μV(x), dove V(x) è una funzione scalare arbitraria. Queste trasformazioni sono dette trasformazioni di gauge (cambiamento di indicatore).
Le trasformazioni di gauge appaiono anche nella teoria della relatività generale di Einstein, e qui corrispondono a una generica trasformazione di coordinate locali. L'invarianza della forma delle equazioni di Einstein porta, attraverso il formalismo di Levi-Civita, a riconoscere che in questo caso l'oggetto matematicamente significativo è il trasporto parallelo, anziché la metrica specifica utilizzata. Conviene pertanto fare intervenire gli operatori differenziali intrinseci Dμ=∂μ+χμ(x), dove in χμ intervengono i simboli di Kristoffel. Definendo una connessione mediante la relazione
[2] Γ aμ,b (x) = Maα(x)(Dμ)αβ M βb(x)
dove M è un campo di matrici che trasforma il sistema di riferimento locale in un sistema di riferimento riemanniano, si vede che le leggi di trasformazione delle connessioni per trasformazioni di Lorentz locali sono descritte dalla relazione
[3] Γμ(x) → h−1(x)Γμ(x)L(x) + L−1(x)∂μL(x).
Si può notare che la [3] è simile alla legge di trasformazione del potenziale elettromagnetico per trasformazioni di gauge; la sola differenza sta nel fatto che nella [3] le γΜ sono matrici, e quindi in generale non commutano tra loro. Nel 1918 Hermann Weyl cercò di utilizzare questa similitudine per costruire una teoria unificata di elettromagnetismo e gravitazione; il tentativo fallì ma, con l'avvento della meccanica quantistica, l'idea di Weyl fu ripresa da Erwin Schrödinger (e contemporaneamente da Fritz Wolfgang London). La funzione d'onda di Schrödinger è a valori complessi e ammette quindi un naturale cambiamento di gauge, costituito da mutamenti locali della fase (un cambiamento globale costante nello spazio non altera lo stato del sistema). Schrödinger ebbe così l'idea di descrivere il moto di una particella quantistica carica in un campo elettromagnetico di potenziale Aμ utilizzando il principio di corrispondenza e sostituendo all'operatore differenziale ∂μ l'operatore differenziale covariante ∂μ+ieAμ (abbiamo indicato con e l'unità di carica elettrica e utilizzato unità di misura in cui la costante di Planck ha valore uno). Nel 1929 Weyl notò che questa prescrizione può essere dedotta dalla condizione che l'equazione di Schrödinger sia invariante per trasformazioni di gauge consistenti nel cambiamento locale della fase della funzione d'onda.
La teoria di gauge ha avuto un notevole sviluppo con l'estensione, compiuta da Chen Ning Yang e Robert L. Mills nei primi anni Sessanta del Novecento, del principio dell'invarianza di gauge al caso di un gruppo G non commutativo; Yang e Mills si interessarono particolarmente al gruppo SU(2) composto da tutte le matrici unitarie di ordine due con determinante uguale a uno. Sebbene la teoria di Yang-Mills sia così formulata in ambito classico, essa è nata dallo studio di problemi quantistici e, precisamente, della teoria delle particelle elementari, classificate mediante rappresentazioni irriducibili del gruppo SU(2), o del gruppo SU(3): la richiesta di invarianza dell'azione lagrangiana per azione locale del gruppo corrisponde alla richiesta di covarianza delle equazioni rispetto a una trasformazione di riferimento per i gradi di libertà interni (che si supponevano responsabili della differenziazione di particelle appartenenti a una stessa famiglia) che non abbia effetto sulle interazioni forti (nucleari).
Il problema che si ponevano Yang e Mills era quello di capire quale forma potesse avere una lagrangiana (classica) che descriveva un campo (classico) ψ(x) ed era invariante sotto l'azione locale ψ(x)→U(g(x))ψ(x), dove g(x) è, per ogni valore della coordinata x, un elemento di un gruppo di Lie, tipicamente SU(2) o SU(3). Nella lagrangiana utilizzata nella teoria dei campi (classica o quantistica) intervengono termini di massa e di potenziale che sono automaticamente invarianti sotto questa trasformazione, ma anche un termine di energia cinetica che contiene in forma quadratica il campo ∂μψ(x). Introducendo, come era stato fatto nel caso dell'elettromagnetismo, un potenziale A(x) (in questo caso a valori nella rappresentazione aggiunta di G) e sostituendo la derivata parziale ∂μ con la derivata parziale covariante ∂μ+ieAμ(x), si vede che, per avere invarianza del funzionale d'azione, e quindi equivarianza delle equazioni della teoria, il campo A(x) deve trasformarsi secondo la legge
[4] A′μ(x) = i∂μ + U*(g(x))(−i∂μ + eAμ(x))U(g(x))
dove U(g(x)) è una rappresentazione unitaria del gruppo G.
A questo punto si è costretti a introdurre una dinamica anche per il campo A(x), che giocherebbe altrimenti il ruolo di moltiplicatore di Lagrange nel principio variazionale, imponendo vincoli al sistema. Yang e Mills hanno dimostrato che, se si richiede che la nuova lagrangiana contenga solamente le derivate di ordine uno del campo A e che la dipendenza da queste sia al più quadratica, in analogia con il termine cinetico della meccanica quantistica, la scelta del termine cinetico di A nella lagrangiana deve essere Tr(FμνFμν), con Fμν=∂μAν+∂ν Aμ+[Aμ,Aν], e Fμν=gμσgνϱFσϱ, dove il simbolo Tr indica l'operatore di traccia. Ne segue che la lagrangiana dell'intero sistema dev'essere Tr(FμνFμν)+L(ψ,Dμψ), dove L è la lagrangiana in assenza di simmetrie interne. La teoria di Yang-Mills è stata anche formulata in un contesto di teoria dei campi quantistica, ma in questo caso ha incontrato notevoli difficoltà formali, non ancora superate, per l'attribuzione di un oggettivo significato matematico ai campi così costruiti, in particolare a causa della presenza di termini ambigui o formalmente infiniti. I maggiori successi della teoria di Yang-Mills si hanno a tutt'oggi nell'ambito della teoria topologica dei campi, una teoria semiclassica che trascura le singolarità locali a favore di aspetti topologici globali.
Un esempio del ruolo che gioca la topologia nella teoria classica, e quindi presumibilmente nel limite semiclassico della teoria dei campi quantistici, si può vedere nel caso della struttura degli istantoni. In uno spazio euclideo a quattro dimensioni la condizione che l'integrale su tutto lo spazio della traccia di FμνFμν sia finito implica che all'infinito il potenziale di gauge abbia la forma Aμ(x)=g−1(x)μg(x), per una funzione arbitraria g(x). Nel caso SU(2), l'applicazione g nella sfera S3 non è topologicamente banale e le classi di equivalenza dei potenziali sui quali l'azione è finita sono classificate dai numeri interi (il terzo gruppo di omologia della sfera S3 è il gruppo dei numeri interi), che in questo contesto rappresentano il grado topologico. L'azione di Yang-Mills può essere scritta nel modo seguente
[5] formula
dove F* è il duale di F (cioè F*μν=Fμν).
Si può verificare che Tr(F*F) è della forma divY, per una funzione Y opportuna, e, pertanto, per il teorema di Gauss il suo integrale sull'intero spazio è un numero intero. Risulta quindi che all'interno di ciascun settore l'espressione ∫d4xTr(F*F) assume valore costante e quindi il valore minimo dell'azione è raggiunto in corrispondenza a campi F tali che F−F*=0. Si osservi che questa è un'equazione differenziale del primo ordine, mentre l'equazione di Yang-Mills è del secondo ordine. Poiché il funzionale di Yang-Mills è differenziabile in corrispondenza alle soluzioni di F=F*, esse sono anche soluzioni dell'equazione di Yang-Mills. Gli istantoni, così come altre strutture topologiche più complesse associate all'equazione di Yang-Mills, per esempio i solitoni e i vortici, sono stati oggetto di studi approfonditi, sia per il loro interesse nella costruzione di teorie di gauge, sia in quanto soluzioni topologicamente non banali di equazioni alle derivate parziali non lineari, e quindi punti critici di funzionali non lineari particolarmente interessanti dal punto di vista topologico.
Recenti sviluppi in dinamica hamiltoniana
Un sistema hamiltoniano con n gradi di libertà e hamiltoniana H0 indipendente dal tempo è detto completamente integrabile se ha n integrali primi (costanti del moto) Ik, con k=1,…,n, che siano indipendenti e in involuzione tra loro, cioè tali che {Ik,Ih}=0 per ogni coppia k,h, dove {.,.} sono le parentesi di Poisson e k≠h. Se la superficie di dimensione n ottenuta fissando i valori numerici di tutti gli Ik è compatta, essa è necessariamente un toro. Si possono introdurre come coordinate n variabili angolari φ1,…,φn coniugate alle Ik ({φh,Ik}=δh,k) e la proiezione del moto su ciascuno di questi angoli è un moto rotatorio uniforme, con frequenza δH/δIk (poiché le frequenze variano con continuità sulla superficie, il moto è genericamente multiperiodico). Molti esempi di sistemi completamente integrabili erano noti già all'inizio del XX sec., e molti altri sono stati costruiti recentemente con nuovi metodi.
Qualora si perturbi, anche di pochissimo, un sistema completamente integrabile, per esempio considerando una hamiltoniana Hε=H0+εH1, con H1 funzione generica delle variabili Ik e φh, il sistema che si ottiene non è più completamente integrabile e anzi ha in generale solo una costante del moto, l'energia, comunque piccolo sia il valore numerico del parametro ε. Sulla superficie Hε=E esiste un insieme, il cui complemento ha misura proporzionale a ε, composto di tori di dimensione n che differiscono di poco da quelli associati a H0, e sui quali il moto è multiperiodico con frequenze che differiscono di poco da quelle associate a H0 e tra loro sufficientemente incommensurabili. La rimanente porzione di Hε=E è occupata da traiettorie che risultano molto più complesse, ma hanno in generale un carattere iperbolico (ogni loro intorno si contrae in alcune direzioni e si espande in altre, in modo tale che il volume totale sia costante). In questa regione il moto appare dunque caotico. Quello che risulta più interessante è che queste due regioni si compenetrano molto finemente, tanto che ciascuna di esse è densa nell'altra (la chiusura di ciascuna di esse è l'intera superficie di energia costante).
Questo fenomeno, descritto dal teorema KAM (dai nomi degli studiosi Andrej N. Kolmogorov, Vladimir I. Arnold e Jürgen Moser, che l'hanno dimostrato in modi diversi e sotto condizioni lievemente diverse su H1), è stato uno dei tratti salienti della ricerca relativa ai sistemi dinamici nel XX secolo. Una formulazione del teorema KAM può essere la seguente. Consideriamo un sistema hamiltoniano a n gradi di libertà, con hamiltoniana H0 e completamente integrabile. Consideriamo nello spazio delle fasi un insieme aperto γ=U×Tn, dove U è un insieme aperto di ℝn con coordinate canoniche I=I1,…,In e Tn è un toro n-dimensionale con coordinate φ=(φ1,…,φn). Consideriamo una piccola perturbazione di H0 della forma Hε=H0(I)+εH1(I,φ,ε), dove la funzione H1 è analitica in Uc×Tn e Uc è un intorno complesso di U. Supponiamo che il determinante jacobiano di H0 rispetto alle variabili Ik sia diverso da zero. Allora, per ε abbastanza piccolo, si può trovare un sottoinsieme Kε in γ tale che la misura di Kε tende alla misura di γ quando ε tende a zero e una partizione misurabile di Kε in tori n-dimensionali invarianti per il flusso di Hε. Su ciascuno di questi tori il moto è multiperiodico con periodi che, quando ε tende a zero, tendono ai periodi del moto descritto da H0. L'insieme Kε non è in generale aperto e il suo complementare è denso in γ. Notiamo che quest'ultima affermazione si può tradurre in termini descrittivi dicendo che Kε è un insieme che a qualunque scala microscopica presenta dei 'buchi'. Ciascuno di questi buchi contiene una regione in cui il moto è multiperiodico e una, di misura relativa di ordine ε, in cui il moto è caotico.
Questa caoticità del moto, che qui appare nei sistemi che differiscono di poco dai sistemi integrabili, era già nota a Jules-Henri Poincaré (1854-1912), che l'aveva analizzata nello studio di sistemi dinamici conservativi perturbati da una forza periodica. Poincaré introdusse il metodo delle varietà stabili e instabili, l'intersezione delle quali contiene orbite omocline, e cercò di studiare questo problema con metodi perturbativi, ma si accorse che le serie perturbative non convergono e che l'angolo tra le varietà è più piccolo di ogni potenza di ε. Poincaré stesso dimostrò che la presenza di un'orbita omoclina implica l'esistenza di infinite altre omocline distinte fra loro e intuì che questo era all'origine del fatto che la dinamica vicino alle omocline fosse caotica. Le argomentazioni di Poincaré erano solamente formali e una buona parte del progresso nella comprensione dei sistemi dinamici nel Novecento è consistito nel dimostrare queste intuizioni di Poincaré per sistemi generali. Una parte cruciale in questo progresso l'hanno avuta prima George D. Birkhoff e poi Stephen Smale. Birkhoff nel 1936 studiò un sistema dinamico ottenuto iterando una trasformazione nel piano che conserva l'area e ha un punto fisso iperbolico tale che le varietà instabile e stabile si intersecano formando un angolo non nullo. Egli dimostrò che questo sistema ha un'infinità (numerabile) di orbite periodiche, che si accumulano sulle omocline. Birkhoff propose anche l'uso della dinamica simbolica, con la quale ogni traiettoria è rappresentata da una serie numerica. La descrizione completa della dinamica in un intorno di un punto fisso omoclino è stata data da Smale, con un modello detto del 'ferro di cavallo' per la struttura geometrica degli insiemi considerati.
Una descrizione completa dell'insieme di orbite che rimangono per tutti i tempi in un intorno di un punto fisso omoclino è stata data soltanto recentemente, nel 2000, da Leonid P. Shil´nikov. Stime quantitative per l'angolo di separazione (che, ricordiamo, è più piccolo di ogni potenza di ε) sono state date da V.K. Melnikov nel 1963, seguendo un metodo proposto da Poincaré per il calcolo dell'angolo di separazione tra la varietà stabile e quella instabile. Altre stime sono state date da Nikolai N. Nekhoroshev nel 1977 e da Anatoly I. Neishtadt nel 1984 perfezionando il classico teorema della media nel tempo. Lo studio delle proprietà delle orbite omocline e dell'angolo di separazione rimane a tutt'oggi lo strumento principale nella definizione e nella descrizione di sistemi caotici. I risultati di Birkhoff sono stati generalizzati da Arnold, che ha dimostrato che l'esistenza di infinite orbite periodiche implica anche l'esistenza di traiettorie che connettono punti dello spazio delle fasi in cui le variabili d'azione, che sono costanti del moto per ε=0, differiscono per una quantità finita (diffusione di Arnold).
Tornando al risultato principale, il teorema KAM, la sua dimostrazione, sebbene complessa e laboriosa nei dettagli, si basa su un'idea relativamente semplice: cercare una successione di trasformazioni canoniche di coordinate nello spazio delle fasi tale che nelle nuove variabili l'hamiltoniana H dipenda solamente dalle variabili d'azione Ik. L'esistenza di tale trasformazione dimostrerebbe che anche il sistema descritto da Hε è completamente integrabile; quindi la successione non può convergere. L'ostacolo all'esistenza della trasformazione cercata deriva dal fatto che la funzione generatrice di tale trasformazione sarebbe una soluzione di una successione di equazioni differenziali di primo ordine; per trovare questa soluzione è necessario invertire un operatore lineare. Lo spettro di quest'operatore ha lo zero come punto di accumulazione e questo permette l'inversione solamente per dati iniziali contenuti nel sottoinsieme Kε dello spazio delle fasi. Questo procedimento di inversione, unito a un'accurata utilizzazione del metodo d'approssimazione di Newton, permette di dedurre un risultato più debole, dovuto a Nekhoroshev, che afferma che le traiettorie che risolvono il sistema hamiltoniano Hε restano, per ε abbastanza piccolo e dati iniziali scelti da un insieme di misura piena, vicine alle traiettorie del sistema H0 per un tempo esponenzialmente lungo.
Il teorema KAM rivela la difficoltà che si incontra nel tentativo di dimostrare la stabilità di un sistema hamiltoniano. In generale si può ottenere una stabilità in misura, la quale assicura che la maggior parte delle traiettorie è stabile per un sistema che differisca poco da uno completamente integrabile. È importante sottolineare che il teorema KAM, nella sua dimostrazione attuale, è insoddisfacente dal punto di vista della fisica matematica. Infatti, i valori del parametro ε per i quali vale il teorema sono di molti ordini di grandezza più piccoli delle perturbazioni che si incontrano in sistemi fisici naturali, come può essere, per esempio, il sistema Terra-Luna-satellite artificiale, in cui il piccolo parametro può essere il rapporto tra la massa del satellite artificiale e la massa della Luna. Solamente con stime più accurate e mediante l'uso di calcolatori elettronici sono stati raggiunti valori di ε più vicini ai sistemi fisici reali.
Un altro problema che ha avuto notevoli sviluppi recenti è quello degli N corpi soggetti a interazioni newtoniane, o che differiscono da un'interazione newtoniana per un termine potenziale regolare. Uno dei problemi in questo ambito riguarda l'esistenza di traiettorie che non siano singolari; le singolarità possono essere di collisione o dovute all'esistenza di un tempo finito nel quale uno o più corpi si sono allontanati all'infinito. L'insieme C dei punti critici del funzionale di azione lagrangiana, se questo è differenziabile in C, fornisce soluzioni dell'equazione del moto. Nel problema a N corpi, e in quelli in cui il potenziale ha comunque singolarità di tipo newtoniano, il funzionale d'azione ammette anche punti critici in cui non è differenziabile, che in generale corrispondono a soluzioni deboli che hanno singolarità. In particolare ci possono essere tempi nei quali un sottoinsieme di corpi entra in collisione. Per un numero limitato di corpi (N〈5) è stato dimostrato che vi sono soluzioni senza collisioni per ogni potenziale con singolarità di tipo newtoniano, ma il problema è ancora aperto per N grande. La ricerca di punti critici del funzionale d'azione ha portato negli ultimi venti anni a un notevole sviluppo di tecniche variazionali, soprattutto in sistemi con vari gradi di simmetria, e a un raffinato uso di metodi topologici. Per il secondo tipo di problemi, interessante è il risultato ottenuto nel 1997 da Xia, che ha dimostrato che per un sistema di cinque corpi, di cui uno di massa molto più piccola degli altri, esistono soluzioni prive di collisioni in cui il corpo più leggero si allontana indefinitamente in un tempo finito. La dimostrazione è molto elaborata e fa massiccio uso della dinamica simbolica; il risultato è interessante perché fa luce sulla complessità del moto newtoniano.
Sistemi dinamici della meccanica statistica
La seconda metà del Novecento ha visto un rinnovato interesse per la meccanica statistica: per trattare sistemi di infinite particelle sono stati introdotti metodi matematici rigorosi e la connessione con i progressi nella teoria della probabilità è divenuta più stretta. Parleremo in modo elementare di alcuni dei risultati più importanti. Innanzi tutto è necessario descrivere la dinamica di sistemi composti da un numero infinito di particelle, che per semplicità supporremo identiche. Se le particelle fossero in numero finito N, la descrizione naturale avverrebbe mediante l'introduzione di uno spazio posizione-velocità con coordinate q1,…,qN, v1,…,vN, che indichiamo collettivamente con il simbolo s. La dinamica sarebbe descritta da una funzione di s, la hamiltoniana
[6] formula
dove U è il potenziale della forza intermolecolare (abbiamo scelto masse unitarie). Supporremo sempre che il potenziale sia una funzione abbastanza regolare. Le equazioni del moto sono le equazioni di Hamilton, con hamiltoniana H(s). Se lo spazio delle configurazioni è tutto ℝ3, in generale il moto è tale che le particelle si allontanano indefinitamente. Per ottenere sistemi con densità finita, richiediamo che tutte le particelle si muovano in una regione ωN il cui volume cresce linearmente con N. Occorre porre delle condizioni al bordo di ωN. Una scelta naturale che noi faremo è che ωN sia un cubo di lato LN, con LN3=N, con condizioni periodiche al bordo per garantire la conservazione di energia e quantità di moto.
Prima di passare alla descrizione della dinamica di un sistema infinito di particelle, conviene osservare che, essendo queste tra loro identiche, possiamo identificare le configurazioni di N particelle con gli insiemi finiti di ℝ3×ℝ3 che contengono N punti. Lo spazio S di un sistema infinito di particelle può allora essere identificato con lo spazio di tutti gli insiemi numerabili di ℝ3×ℝ3 localmente finiti, nel senso che ogni cubo λn di lato finito in ℝ3 contiene un numero finito di questi punti. Una topologia naturale in S è la seguente: una successione di insiemi sm converge a una realizzazione s se, per ogni intero n, il numero di punti nell'insieme sm contenuti in λn per m abbastanza grande coincide con il numero di punti dell'insieme s contenuti in λn, e per ogni n, sm∩λn converge a s∩λn quando m tende all'infinito. Se chiamiamo Tt(s∣λn) la realizzazione in s∣λn della dinamica associata al cubo λn con condizioni periodiche al bordo, definiamo la dinamica del sistema infinito mediante il limite (se esiste) Tt(s)=limn→∞Tt(s∣λn).
Il limite indicato non esiste per tutte le configurazioni s: per qualche configurazione del sistema infinito, tutte le particelle potrebbero, per esempio, concentrarsi in uno stesso punto dello spazio in un tempo finito. Lo studio delle condizioni sul potenziale affinché siano sufficientemente numerose le configurazioni per le quali il limite esiste per ogni tempo, in modo tale che esse costituiscano un insieme di misura piena per le distribuzioni di interesse, è tuttora una parte importante della ricerca in questo campo. Una volta introdotta la dinamica di un sistema di infinite particelle, si può cominciare a parlare di evoluzione di insiemi statistici e della loro eventuale invarianza. Denotiamo con S0 il sottoinsieme di S per il quale la dinamica esiste per ogni tempo e consideriamo una misura di probabilità P0 in S che sia portata tutta da S0; l'evoluzione di P0 è data da Pt(Q)=P0({s: (Tt (s) in Q)}) per ogni sottoinsieme misurabile Q di S. Possiamo ora formulare il postulato di Gibbs nel modo seguente: per una vasta classe di stati iniziali P0 lo stato Pt tende, quando t tende all'infinito, a uno stato di Gibbs corrispondente al potenziale U che descrive la dinamica del sistema. Diamo qui la definizione di stato di Gibbs nel contesto di un sistema che contenga un numero infinito di particelle. Fissato un parametro β e un vettore w, la distribuzione di Gibbs è tale che in ogni volume finito ω la misura dell'insieme SN(ω) è definita dalla densità seguente rispetto alla misura di Lebesgue:
[7] formula
dove ZN−1 è un fattore di normalizzazione (funzione di partizione).
Come si può vedere, in questo insieme le velocità sono mutuamente indipendenti e hanno distribuzione maxwelliana. La misura definita dalla [7] è una misura prodotto. Definiamo misura di Gibbs configurazionale la restrizione della misura [7] alle funzioni delle sole variabili di posizione. Poiché le misure gaussiane ammettono un limite naturale quando il numero di coordinate tende all'infinito, nel seguito studieremo solamente il limite della misura di Gibbs configurazionale. Una misura nello spazio S è detta misura di Gibbs (associata a un potenziale U) se è il limite di misure di Gibbs con potenziale U in una successione di regioni di volume crescente che invadono ℝ3, con condizioni a bordo opportune, oppure fa parte della chiusura convessa di tali limiti. Per valori del parametro β sufficientemente piccoli la misura di Gibbs, se esiste, è unica e può essere costruita con un metodo iterativo (sviluppo a grappoli). Ci si aspetta che in dimensioni spaziali maggiori di uno e per valori abbastanza grandi del parametro β (e per temperature abbastanza piccole) la misura di Gibbs così definita non sia unica e le misure ottenute con il processo di limite dipendano dalle condizioni al bordo scelte, ma nessuna di queste affermazioni è stata finora dimostrata in modo rigoroso.
È stato dimostrato che, per un vasta classe di potenziali U, la misura di Gibbs associata è invariante per la dinamica data dal potenziale U stesso: risultato banale per insiemi finiti di particelle, ma meno ovvio nel caso di insiemi infiniti. È stato d'altra parte dimostrato che le misure di Gibbs con potenziale U non esauriscono in generale la classe dei sistemi a infinite particelle invarianti per la dinamica generata dal potenziale U; ricordiamo, a titolo di confronto, che nel caso di un numero finito di particelle possono esistere altri integrali primi del moto oltre all'energia, e inoltre è possibile definire altri ensemble invarianti, come, per esempio, l'ensemble microcanonico. D'altra parte è possibile porre altre condizioni naturali sulle misure invarianti rispetto alla dinamica associata a un potenziale U. Per esempio si può richiedere l'invarianza per traslazioni spaziali, o ammettere densità, rispetto alla misura di Lebesgue, se ristrette a un volume finito, o ancora avere la proprietà di indipendenza spaziale asintotica forte, ossia che il valore atteso del prodotto di due funzioni, ciascuna delle quali dipenda solamente dalla configurazione in regioni finite O1 e O2 dello spazio, tenda al prodotto dei corrispondenti valori attesi quando la distanza tra O1 e O2 tende all'infinito. Si può formulare la congettura che queste ulteriori condizioni identifichino lo stato di Gibbs relativo al potenziale U.
Un importante contributo in questa direzione è stato dato recentemente da Yakov G. Sinai e dai suoi collaboratori, che hanno dimostrato un caso particolare di questa congettura facendo uso di un metodo introdotto da Nikolai N. Bogoljubov alla fine degli anni Cinquanta del Novecento, che consiste nello studiare la misura in esame mediante l'analisi dei suoi momenti (funzioni di correlazione). Parte di questa dimostrazione consiste nel provare che le sole leggi di conservazione (in media) sono quelle dell'energia e della quantità di moto, come nel caso di un numero finito di particelle in un contenitore a pareti riflettenti. Un'altra affermazione che non ha avuto finora una dimostrazione completa è l'equivalente, per i sistemi di infinite particelle, dell'affermazione di Gibbs secondo cui le misure di Gibbs sono il limite, per t→∞, di qualunque misura (regolare) che evolva secondo una dinamica hamiltoniana con potenziale U regolare. Tale risultato è stato dimostrato da K.L. Volkovissky e Sinai nel 1971 nel caso del modello di un gas di sfere rigide (con naturali condizioni di rimbalzo negli urti) e nel caso unidimensionale di interazioni per urto elastico di bastoncini rigidi; si noti che in entrambe le situazioni non si tratta di dinamiche originate da un potenziale regolare. Questa proprietà è un analogo del mescolamento per sistemi dinamici con un numero finito di gradi di libertà.
È anche possibile formulare una congettura sulla convergenza di una misura regolare a una misura di Gibbs in media nel tempo, l'equivalente dell'ipotesi ergodica nel caso di dimensione finita. La congettura potrebbe essere espressa nel seguente modo:
[8] formula
dove P è una misura di Gibbs, f è regolare e la convergenza è intesa come convergenza in probabilità. Nel caso di dimensione finita, l'ipotesi ergodica è messa in dubbio dal risultato di Lawrence Markus e Kenneth R. Meyer, che nel 1978 hanno dimostrato che nello spazio delle hamiltoniane regolari quelle che soddisfano l'ipotesi ergodica hanno misura nulla; non vi è motivo di dubitare che questo risultato, con le dovute precisazioni, sia vero anche per i sistemi di dimensione infinita. D'altra parte, l'ipotesi ergodica non è né necessaria né sufficiente per la dimostrazione della formula [8] per sistemi composti da un numero infinito di particelle, e quindi per la meccanica statistica. Se si considerano i sistemi ai quali si interessa la meccanica statistica come limiti di sistemi con un numero finito N di particelle, è sufficiente che i sistemi approssimanti siano 'approssimativamente ergodici'. Roland Dobrushin ha ipotizzato che per N molto grande questi sistemi abbiano moltissime piccole componenti ergodiche, distribuite in modo così complesso da non poter essere distinte con osservazioni macroscopiche in una frazione del volume totale. Naturalmente questa congettura è di difficile formulazione e di ancora più difficile dimostrazione.
Teoremi, e non congetture, possono essere enunciati e dimostrati lasciando cadere l'ipotesi che ciascuna delle regioni spaziali O considerate contenga un numero fissato, N(O), di particelle. Introduciamo un parametro z, che chiamiamo fugacità, e supponiamo che N(O) sia una variabile casuale distribuita secondo la misura di Poisson di parametro z. Le variabili N(O) al variare di O sono allora tra loro indipendenti e ciascuna di esse è distribuita secondo la legge
[9] P({q, N(O)=k)} = k−1(zL(O))kexp(−zL(O))
dove L(O) è la misura di Lebesgue di O. Con queste notazioni l'ensemble grancanonico associato al potenziale U con parametri z e β è definito dalla legge di probabilità [9] per quanto riguarda la variabile N(O), e la legge di probabilità condizionale, dato N(O), coincide con la misura di Gibbs (configurazionale) definita precedentemente.
Per la distribuzione gran-canonica si possono dimostrare vari teoremi. Assumiamo che il potenziale U soddisfi le seguenti condizioni: (a) sia limitato inferiormente; (b) sia regolare nell'origine; (c) decresca all'infinito in valore assoluto secondo una potenza sufficientemente grande dell'inverso della distanza. Sotto queste ipotesi, si può dimostrare che: Teorema 1: per fissati z e β maggiori di zero, esiste almeno una misura di Gibbs (gran-canonica) invariante per traslazioni, con potenziale U e parametri z e β. Tali misure formano un insieme convesso e compatto. Teorema 2: per ogni ε>0 esiste un valore z0(ε) tale che per ogni z, 0〈z〈z0(ε), esiste una sola misura gran-canonica di Gibbs con potenziale U e parametri z e ε. La distribuzione di questa misura è invariante per traslazioni spaziali e soddisfa la proprietà di mescolamento asintotico spaziale forte. Inoltre è possibile dimostrare che i momenti di questa misura (funzioni di correlazione) soddisfano un sistema di equazioni (equazioni DLR, dai nomi Dobrushin, Lanford e Ruelle) che per valori sufficientemente piccoli dei parametri possono essere risolte in modo iterativo.
È interessante notare che gli insiemi, in cui per ogni regione dello spazio è fissato il numero di particelle, hanno misura grancanonica nulla; pertanto dai teoremi precedenti non si può trarre alcuna indicazione sull'esistenza di una misura canonica di Gibbs nel caso di un numero infinito di particelle. Risposte più soddisfacenti riguardanti la dinamica e la misura canonica di Gibbs si sono ottenute in modelli di sistemi di infinite particelle nei quali la dinamica è retta da leggi casuali (per es., da processi di tipo Markov). Risultati migliori sono stati derivati in modelli nei quali lo spazio ℝ3 viene sostituito da un reticolo infinito, sui punti del quale possono trovarsi le variabili che assumono valori in un compatto (in questo caso si parla di modelli di spin). In questi modelli la dinamica è costituita da iterate di un'applicazione di Markov, che a ogni configurazione ne sostituisce un'altra secondo regole stocastiche prefissate. Nel caso in cui l'insieme compatto sia composto da due punti, come, per esempio, nel modello di Ising, o da un numero finito di punti (modelli di Potts), si sono ottenuti risultati abbastanza completi riguardo all'esistenza di una transizione di fase (perdita di unicità della misura di Gibbs) per valori del parametro β superiori a una data soglia, e interessanti informazioni sulla struttura della misura di Gibbs alla soglia (struttura di percolazione, esponenti critici, ecc.).
Dalla meccanica quantistica alla teoria quantistica dei campi
La meccanica quantistica non relativistica, sebbene risulti adeguata a descrivere la struttura atomica e molecolare, appare insufficiente a descrivere le interazioni tra particelle e campo elettromagnetico. L'effetto fotoelettrico, combinato con il dualismo onda-particella, porta ad associare al campo elettromagnetico i fotoni, particelle di massa nulla, il cui numero è suscettibile di variazione a causa dell'interazione con la materia. Ciò rende il formalismo di Schrödinger, in cui il numero di particelle è costante, inadatto alla trattazione del campo elettromagnetico e individua lo spazio funzionale nel quale scrivere le equazioni, vale a dire lo spazio delle funzioni a quadrato integrabile su ℝ3n, se si considera un sistema di n particelle in dimensione spaziale 3. Nel vuoto, ciascuna componente del campo elettromagnetico soddisfa l'equazione delle onde; se la dimensione spaziale è 1, si impongono condizioni periodiche relative al segmento di estremi 0-L e si utilizza lo sviluppo in serie di Fourier, l'equazione delle onde appare come equazione per infiniti oscillatori armonici, ciascuno con frequenza nL−1, avendo scelto un sistema di unità di misura in cui la velocità della luce è eguale a 1. L'equazione di evoluzione per ciascuno di questi oscillatori è hamiltoniana e la corrispondente hamiltoniana quantistica, ottenuta con le regole di quantizzazione di Heisenberg e Schrödinger, ha come autofunzioni i polinomi di Hermite Hn e autovalori multipli di nL−1 (a meno di una traslazione per una costante).
È possibile allora interpretare lo stato Hn come stato a n particelle, i fotoni di energia nL−1, e la conseguente descrizione dello spazio di Hilbert associato al campo elettromagnetico 'quantizzato' come somma diretta di spazi, parametrizzati da un indice n intero, ciascuno descritto in termini di numero di occupazione di fotoni di frequenza nL−1 e energia assegnate. Questa descrizione, detta rappresentazione di Fock, da Vladimir A. Fock che la suggerì in questa forma alla metà degli anni Trenta del Novecento, è detta seconda quantizzazione, laddove prima è la formulazione della meccanica quantistica di Heisenberg e Schrödinger. A questa formulazione è associata la parola quantizzazione in quanto gli aspetti quantistici che essa descrive sono connessi (sebbene non dal punto di vista analitico) al fatto che i livelli energetici degli atomi sono quantizzati.
La rappresentazione di Fock, posta in una forma matematicamente più precisa da Valentine Bargmann e soprattutto da Irving E. Segal nei primi anni Sessanta del Novecento, è alla base della teoria dei campi quantizzati. Nell'esposizione che ne abbiamo dato si è supposto che lo spazio fosse unidimensionale e si sono poste condizioni periodiche agli estremi di un segmento. La formulazione può essere facilmente generalizzata al caso di ℝ3. In questa rappresentazione un ruolo importante hanno gli operatori di creazione e di distruzione associati a un grado di libertà, la cui azione consiste nel far passare il sistema da uno stato a un altro nel quale il numero di fotoni è aumentato o diminuito di una unità. Gli operatori che rappresentano il campo e la sua derivata rispetto al tempo sono ottenuti mediante somma e differenza degli operatori di creazione e distruzione, con coefficienti atti a riprodurre le proprietà di covarianza del campo e a far sì che il campo stesso soddisfi le equazioni di Maxwell (che, ricordiamo, sono equazioni iperboliche e quindi richiedono per la risoluzione i dati del campo e della sua derivata temporale in un istante prefissato).
Questa interpretazione permette di studiare interazioni in cui non sia conservato il numero di fotoni e quindi di analizzare fenomeni come l'effetto fotoelettrico. L'interazione della materia, nei suoi aspetti non relativistici, con il campo elettromagnetico quantizzato, è ora descritta in termini di una hamiltoniana somma di una parte libera (la somma delle hamiltoniane non interagenti rispettivamente del campo e delle particelle) e di una hamiltoniana d'interazione, che in generale si sceglie lineare negli operatori di creazione o di distruzione del campo, con coefficiente proporzionale all'operatore che rappresenta la corrente (una costruzione che corrisponde alla quantizzazione dell'interazione del campo elettromagnetico classico con le correnti). Poiché il coefficiente di proporzionalità è la carica elettrica e, che in unità naturali risulta molto piccola (1/137 ca.), si può pensare di adottare un metodo perturbativo per la risoluzione dei problemi, sebbene, in conseguenza del carattere singolare dell'interazione a frequenze elevate (a piccole distanze), la serie perturbativa presenti in generale difficoltà formali, sotto forma di divergenze di integrali, che vanno risolte con opportuni artifici (che vanno sotto il nome di rinormalizzazione) per ciascun ordine in e. Recentemente sono stati fatti considerevoli progressi in una trattazione non perturbativa della teoria, in particolare per quanto riguarda modelli semplificati (modelli di Pauli-Fierz), ma una trattazione completa non è stata ancora elaborata.
La trattazione perturbativa dell'elettrodinamica quantistica relativistica ha condotto a previsioni che sono state confermate dai dati sperimentali con un eccezionale grado di precisione e alcune difficoltà teoriche, connesse all'ambiguità nel prodotto di distribuzioni, sono state superate grazie a un'accurata analisi microlocale di fronti d'onda. Sembra ragionevole pensare che, termine a termine, sia possibile dare una trattazione matematica completa, anche se ciò non è stato fatto finora. D'altra parte, la serie perturbativa non soddisfa alcuno dei criteri di convergenza, anche debole (convergenza di Borel), per cui non è chiaro attualmente se questa serie corrisponda a una soluzione ben definita. La teoria delle perturbazioni, nell'ambito di una teoria di campo quantistica, ha avuto un notevole sviluppo a partire dagli anni Cinquanta del Novecento, con contributi importanti, tra gli altri, di Julian Schwinger, Sin-Itiro Tomonaga, Freeman Dyson, Nikolai N. Bogoljubov e soprattutto Richard P. Feynman; la prescrizione di Feynman in termini di diagrammi per il calcolo dei valori dei campi e della matrice S (che descrive i fenomeni di scattering) attesi nel vuoto è tuttora alla base della maggior parte dei lavori in questo settore e ha prodotto risultati di notevole valore, anche dal punto di vista matematico.
In seguito al successo, almeno perturbativo, dell'elettrodinamica quantistica e in base al principio di dualità onda-particella, sono state proposte, per lo studio delle particelle elementari, teorie che introducono campi associati a ciascuna particella e un'interazione dedotta quantizzando i campi di particelle, sulla falsariga della quantizzazione del campo elettromagnetico. Sono quindi introdotti anche per le particelle operatori di creazione e distruzione, e un opportuno stato di vuoto, corrispondente al numero di occupazione zero per tutte le particelle. I campi introdotti sono di varia natura: scalare, vettoriale o comunque a spin intero oppure spinoriale (per particelle di spin semi-intero, questi ultimi corrispondono a rappresentazioni irriducibili di dimensione pari del gruppo SU(2)). La loro quantizzazione utilizza, analogamente a quanto fatto per il campo elettromagnetico, relazioni di commutazione canonica per particelle di spin intero, corrispondenti a relazioni di commutazione per i campi in regioni spazialmente separate a un tempo fissato, o a relazioni di anticommutazione canonica per particelle di spin semi-intero, corrispondenti a campi che anticommutano. Per questi ultimi, è facile mostrare che il numero di occupazione per ciascun grado di libertà può assumere solamente i valori 0 o 1, in accordo con il principio di esclusione di Pauli.
Nella descrizione fornita dalla teoria dei campi quantizzati delle interazioni forti tra particelle elementari, le costanti di accoppiamento sono molto grandi, dell'ordine di grandezza di 10 in unità naturali (sebbene la definizione stessa di costante d'accoppiamento sia incerta, a causa delle ambiguità che presenta una trattazione rigorosa) e il valore predittivo di una serie perturbativa risulta incerto per valori così grandi del parametro di sviluppo. D'altra parte, fino all'inizio degli anni Settanta del Novecento il solo esempio di teoria di campo quantistica rigorosamente formulata era la teoria di campo libera, interessante dal punto di vista matematico ma di scarsa rilevanza fisica. Questa teoria era stata costruita da Kurt Otto Friedrichs e da Segal negli anni Cinquanta del secolo scorso, ed era definita sullo spazio di Fock. Diamo qui alcuni dettagli per il caso del campo scalare di massa m. Il campo φ(x) è costruito come distribuzione a valori operatoriali, che soddisfa l'equazione (∂2+m2)φ(x)=0, dove ∂2 è l'operatore di Laplace. Il campo φ(x) soddisfa inoltre le relazioni di commutazione (canoniche) [φ(x), φ(x′)]=iD(x−x′), x={x0=ct, x1, x2, x3}, dove D(y) è la soluzione reale dell'equazione ∂2D=0 che si annulla all'esterno del cono di luce. Dall'equazione che soddisfa si deduce che il campo stesso può essere scritto come somma di una parte a frequenza positiva e di una a frequenza negativa. Questo campo può essere realizzato in uno spazio di Fock che ha uno stato ω (il vuoto) 'annichilato' dalla parte a frequenze negative, mentre i polinomi nella parte a frequenza positiva generano un insieme denso se applicati a ω. Le equazioni soddisfatte dal campo sono hamiltoniane e la corrispondente energia è positiva, e si annulla soltanto in corrispondenza del vuoto.
Questa costruzione può essere considerata la quantizzazione alla Fock della dinamica simplettica definita sulla varietà lineare delle soluzioni classiche dell'equazione delle onde. Per trattare una teoria con interazione, nei primi anni Sessanta Segal tentò, ma senza successo, di quantizzare la dinamica simplettica definita sulla varietà (non più lineare) delle soluzioni dell'equazione delle onde con un termine non lineare. Nello stesso periodo Arthur S. Wightman formulò una teoria assiomatica per i campi quantistici relativistici, basata sulle ipotesi di località, esistenza del vuoto e positività dell'energia (definita come generatore del gruppo unitario che descrive le traslazioni nel tempo). Come conseguenza degli assiomi, le funzioni W(x1,…,xn)=(ω,φ(x1),φ(xn)ω) (funzioni di Wightman) hanno proprietà di invarianza, di positività (conseguenza della positività del prodotto scalare hilbertiano) e di analiticità (conseguenza dell'ipotesi di positività dello spettro dell'energia). Wightman dimostrò anche che il campo può essere 'ricostruito' completamente quando si conoscano le funzioni W(x1,…,xn).
Una teoria assiomatica simile fu poco dopo suggerita da Rudolph Haag, facendo uso di algebre di operatori limitate associati a ogni regione limitata dello spazio-tempo, con naturali condizioni di inclusione e di commutatività a distanze 'spaziali'. Anche Haag postulava l'esistenza di un generatore del gruppo delle traslazioni temporali, con spettro contenuto nel semiasse positivo e un autovalore zero isolato e non degenere (il corrispondente autovettore è il vuoto). Queste teorie assiomatiche hanno un contenuto matematico notevole e sono state preziose per delineare le caratteristiche generali di una teoria quantistica dei campi, ma lasciano insoluta, come accadeva nella teoria perturbativa, la domanda se possano esistere teorie di campo quantistiche relativistiche diverse dalla teoria dei campi liberi. Le funzioni di Wightman hanno proprietà di analiticità (in conseguenza della positività dell'energia) che ne permettono il prolungamento analitico in regioni dello spazio-tempo complesso che contengano l'insieme nel quale tutte le variabili tempo assumono un valore immaginario. Questo permette di introdurre alcune funzioni, dette di Schwinger, definite sullo spazio euclideo anziché su quello di Minkowski, ed è possibile formulare una teoria assiomatica anche per le funzioni di Schwinger. Konrad Osterwalder e Robert Schrader hanno dimostrato che a ogni teoria euclidea così formulata corrisponde in modo biunivoco una teoria minkowskiana di Wightman e pertanto la costruzione di una teoria di campo relativistica può essere sviluppata mediante costruzione esplicita di una funzione di Schwinger.
Queste funzioni hanno caratteristiche di positività puntuali, messe in luce soprattutto da Kurt Symanzik, che ne rendono possibile l'interpretazione come funzioni di transizione per un processo stocastico. Seguendo queste interpretazioni, nel 1971 Edward Nelson è riuscito a costruire un processo stocastico in ℝ1 a cui sono associate funzioni di Schwinger che, prolungate nel piano complesso, danno origine a funzioni di Wightman soddisfacenti gli assiomi. Il campo quantistico relativistico corrispondente è definito su uno spazio-tempo minkowskiano di dimensione due e soddisfa l'equazione (∂2+m2)Φ(x)=:P(Φ(x)): dove P è un polinomio di grado dispari con coefficiente del termine di grado più alto negativo e il simbolo : : indica che le distribuzioni non formano un'algebra, per cui il loro prodotto va interpretato in modo opportuno. Nell'equazione precedente, il campo :P(Φ(x)): è locale.
Seguendo un procedimento diverso, un anno più tardi James Glimm e Arthur Jaffe hanno costruito lo stesso campo facendo uso di metodi della meccanica statistica, ma lavorando direttamente nello spazio di Minkowski. Generalizzando in modo considerevole il metodo seguito da Glimm e Jaffe, qualche anno più tardi Jacques Magnen e Roland Seneor sono riusciti a costruire una teoria quantistica in uno spazio di Minkowski di dimensione 3 (e quindi di dimensione spaziale 2), che è la quantizzazione di una teoria classica associata all'equazione (∂2+m2)φ(x)=g:φ3(x): con g costante negativa (chiamata teoria φ4 per l'espressione formale del potenziale corrispondente). Per polinomi di grado maggiore di tre, e per uno spazio di Minkowski di dimensione quattro, la teoria non è stata ancora costruita e ci sono indicazioni che la teoria quantistica φ4 non sia costruibile, almeno con i metodi utilizzati finora, a causa dell'eccessiva singolarità dei termini. Questo renderebbe più interessante la costruzione rigorosa di una teoria di gauge quantistica.
Bibliografia
Arnold 1988: Arnold, Vladimir I. - Kozlov, Valerii V. - Neish-tadt, Anatoly I., Dynamical systems III, in: Encyclopaediaof mathematical sciences, Berlin-London, Springer, 1988, pp. 1- 287.
Buchholz 2001: Buchholz, David, Algebraic field theory, a status report, in: Proceedings of the XIII Congress of mathematical physics, edited by Alexander Grigoryan e altri, London-Somerville (Mass.), International Press of Boston, 2001, pp. 31-47.
Dobrushin 1989: Dobrushin, Roland - Sinai, Yakov - Sukhov, Yuri, Dynamical systems II, in: Encyclopaedia of mathematical sciences, Berlin-London, Springer, 1989, pp. 208-281.
Faddeev, Slavnov 1991: Faddeev, Ljudvig D. - Slavnov, Andrej A., Gauge fields: introduction to quantum theory, edited by D.B. Pontecorvo, 2. ed., Reading (Mass.), Perseus Books, 1991, pp. 1-28 (1. ed.: Reading (Mass.)-London, Benjamin/Cummings, 1980).
Glimm, Jaffe 1987: Glimm, James - Jaffe, Arthur, Quantum physics, New York, Springer, 1987 (1. ed.: 1981).
Haag 1996: Haag, Rudolph, Local quantum physics, Berlin-London, Springer, 1996 (1. ed.: 1992).
Moser 1998: Moser, Jürgen, Dynamical systems: past and present, in: Proceedings of the International congress of mathematicians, edited by Gerd Fischer, Rosenheim, Geronimo, 1998, pp. 381-402.
Nekhoroshev 1977: Nekhoroshev, Nikolai N., An exponential estimate of the time of stability of nearly-integrable Hamiltonian systems I, "Russian mathematical surveys", 32, 1977, pp. 1-65.
Ruelle 1969: Ruelle, David, Statistical mechanics, Reading (Mass.)-London, Benjamin, 1969.
Taylor 2001: Gauge theories in the twentieth century, edited by John C. Taylor, London, Imperial College, 2001, pp. 1-110.