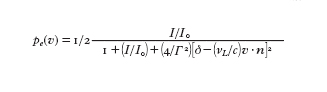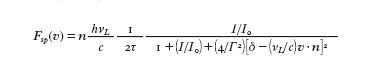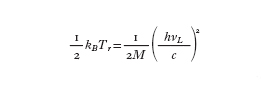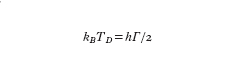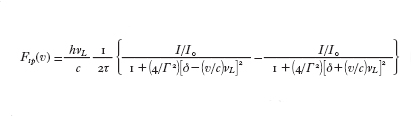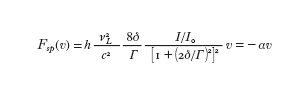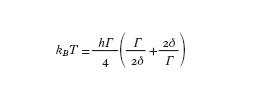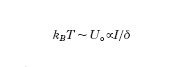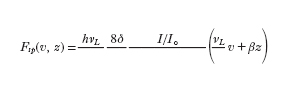Fisica atomica

Fisica atomica

(App. IV, i, p.817)

Le conoscenze sulla struttura atomica, divenuta una parte fondamentale della fisica del 20° secolo a partire dalle classiche esperienze di E. Rutherford del primo decennio, trovano nell'Enciclopedia Italiana un'ampia e specifica trattazione sia negli articoli di E. Fermi (v. atomo: Teoria elettrica dell'atomo, V, p. 243; App. I, p.187), sia in quello di G. Bernardini (v. fisica atomica, App. IV, i, p.817), fino alle più recenti acquisizioni illustrate nella presente voce. Le tecniche affrontate permettono di ottenere campioni particolarmente adatti a indagini spettroscopiche di altissima risoluzione, che si dimostrano utili per la verifica dei fenomeni di condensazione di Bose-Einstein. Da non dimenticare, inoltre, le connessioni con i settori della fisica concernenti la meccanica quantistica (v. quantistica, meccanica, App. IV, iii, p. 119), l'analisi molecolare (v. molecola, App. II, ii, p.338) e spettroscopica (v. spettroscopia, App. V, v, p.102), nonché gli studi sulla struttura nucleare (v. nucleo atomico, App. IV, ii, p. 624). *

Raffreddamento di atomi con luce laser e condensazione di Bose-Einstein

di Massimo Inguscio, Guglielmo M. Tino

In un gas, gli atomi si muovono in tutte le direzioni con velocità che dipendono dalla temperatura. A temperatura ambiente, la velocità degli atomi è dell'ordine di 10041000 m/s, a seconda della massa atomica.

In molti esperimenti è necessario avere atomi con velocità molto basse ed elevate densità, senza che questo causi una variazione delle proprietà intrinseche degli atomi investigati. Il metodo di raffreddamento basato sulle collisioni degli atomi con le pareti di un contenitore freddo è limitato a temperature al di sopra di quella di condensazione del gas. Invece le tecniche di raffreddamento laser, in cui si fanno interagire gli atomi con la radiazione emessa da un laser, permettono di raggiungere temperature estremamente basse, fino al milionesimo di kelvin. Le proprietà di coerenza della radiazione emessa da un laser ne fanno un sistema che si può considerare a bassissima temperatura. L'idea alla base del raffreddamento laser è di diminuire l'energia cinetica degli atomi trasferendo parte dell'energia di questi al campo elettromagnetico. Con tali tecniche gli atomi raffreddati possono inoltre essere confinati in 'trappole' delimitate non da pareti materiali ma da campi elettromagnetici.

Le tecniche di raffreddamento e intrappolamento di atomi permettono quindi di ottenere atomi con velocità molto basse, elevate densità e non affetti da collisioni con le pareti del contenitore. Si ha quindi un campione ideale per esperimenti di spettroscopia ad alta risoluzione, di fisica delle collisioni, di ottica atomica. Questi metodi hanno permesso recentemente di osservare direttamente un fenomeno, detto condensazione di Bose-Einstein, previsto da Einstein nel 1924. L'osservazione della condensazione di Bose-Einstein è stato uno dei risultati più lungamente inseguiti dalla ricerca sperimentale del 20° secolo, ottenuto per la prima volta nel 1995 da E.A. Cornell e collaboratori in un gas di atomi di rubidio.

Raffreddamento e confinamento di atomi con luce laser

Lo studio del raffreddamento e confinamento di atomi con luce laser ha costituito uno dei campi più attivi della ricerca in f. a. nell'ultimo decennio. Si basa su un sapiente utilizzo dell'impulso scambiato tra il fotone e l'atomo durante i processi di assorbimento e di emissione di luce e ha portato a notevoli successi coronati dall'assegnazione del premio Nobel per la fisica nel 1997 a C. Cohen-Tannoudji, S. Chu e W.D. Phillips. Di seguito vengono illustrati gli aspetti più rilevanti del fenomeno e le tappe sperimentali più significative.

Quando un atomo di massa M assorbe o emette un fotone di frequenza ν, per il principio di conservazione della quantità di moto deve variare la sua velocità di una quantità, detta velocità di rinculo, v_r5hν/(Mc), dove h è la costante di Planck e c è la velocità della luce nel vuoto; hν/c è infatti l'impulso del fotone. Per es., nel caso della transizione D₂ in un atomo di sodio (lunghezza d'onda λ5589 nm, M523 u) si ha v_r53 cm/s. Per la transizione D₂ dell'atomo di cesio (λ5852 nm, M5133 u) si ha v_r53,5 mm/s. Questi esempi mostrano che la variazione di velocità, seppur piccola, non è trascurabile. Se infatti si considera un fascio termico di atomi di sodio con una velocità tipica v₀,1000 m/s e un fascio laser che si propaga in direzione opposta a quella degli atomi, perché un atomo si arresti è sufficiente che esso assorba un numero di fotoni N_f5v₀/v_r,33.000. Nel caso del cesio, il numero di fotoni richiesto per arrestare un atomo con velocità iniziale di 300 m/s è circa 86.000. Dopo l'assorbimento di ogni fotone, l'atomo dovrà diseccitarsi prima di poter assorbirne un altro. L'emissione di un fotone in un processo di emissione spontanea avviene in una direzione casuale e quindi, in media, non varia la velocità dell'atomo. Un ciclo di assorbimento e riemissione può impiegare un tempo dell'ordine della vita media τ dello stato eccitato dell'atomo. Per le transizioni considerate si ha τ,20 ns. Per assorbire il numero di fotoni sufficienti ad arrestarsi agli atomi bastano, perciò, pochi millisecondi. Il tempo effettivamente impiegato dipende, oltre che dal valore di τ, da diversi fattori quali la frequenza e l'intensità della radiazione laser.

Per studiare in maggior dettaglio l'interazione tra gli atomi e la radiazione laser, consideriamo un modello semplice di un atomo con soli due livelli, uno fondamentale e uno eccitato, di energie E_f ed E_e separate di una quantità E_e2E_f5hν_A; l'atomo interagisce con un'onda piana di frequenza ν_L e intensità I che si propaga nella direzione indicata dal versore n. Indichiamo con v la velocità dell'atomo e con δ5ν_L2ν_A la differenza tra la frequenza del laser e la frequenza di risonanza atomica. Chiamiamo, inoltre, Γ51/(2χτ) la larghezza naturale (in Hz) della risonanza atomica dovuta alla vita media finita τ dello stato eccitato. Il numero di cicli di assorbimento e riemissione spontanea di fotoni in un secondo è dato dal tasso di emissioni spontanee 1/τ moltiplicato per la probabilità di occupazione dello stato eccitato. Per un atomo, la probabilità p_e(v) di essere eccitato è:

[1] formula

dove I₀ è detta intensità di saturazione. La quantità d_eff5[δ2(ν_L/c) v?n] rappresenta il disaccordo effettivo della frequenza del laser dalla frequenza di risonanza dell'atomo, dovuto sia alla differenza tra la frequenza del laser e quella propria dell'atomo fermo, sia all'effetto Doppler causato dal moto dell'atomo. Come si è detto, ogni ciclo di assorbimento e riemissione di un fotone trasferisce in media all'atomo un impulso hν_L/c, pari a quello di un fotone. Si può allora definire la forza F_sp, detta forza spontanea o forza per pressione di radiazione, esercitata dalla radiazione sull'atomo; essa è data dalla variazione della quantità di moto dell'atomo nell'unità di tempo, ossia dall'impulso trasferito da un fotone moltiplicato per il numero di cicli assorbimento-emissione spontanea nell'unità di tempo. Utilizzando la [1], si ha allora:

[2] formula

La [2] rappresenta la forza media sull'atomo durante diversi cicli di assorbimento-emissione. L'espressione ricavata ha senso purché d_eff non vari molto durante questo tempo, in modo da poter parlare di una forza media. Come si vede dalla [2], questa forza ha un valore limite F_max5hν_L/(2τc) per alte intensità della radiazione (I@I₀). Questo limite è dovuto appunto al tempo minimo, dell'ordine di 2τ, necessario per un ciclo di assorbimento-emissione spontanea. L'accelerazione massima di un atomo dovuta a questa forza è a_max5F_max/M5hν_L/(2Mcτ). Nel caso di un atomo di sodio, per es., si ha a_max,10⁶ m/s²,10⁵ g, con g accelerazione di gravità. Accelerazioni così elevate permettono, come si è detto, di fermare un atomo con una velocità iniziale v_in,1000 m/s in un tempo T_stop5v_in/a_max di solo qualche millisecondo in uno spazio L_stop5(1/2)a_maxT²_stop tipicamente inferiore a un metro.

Nella realizzazione di un esperimento di frenamento sorgono però alcuni problemi trascurati in questo modello. I principali sono la struttura reale di un atomo, che non ha solo due livelli energetici, e la variazione del disaccordo effettivo d_eff della frequenza del laser al variare della velocità dell'atomo. Le soluzioni trovate per risolvere questi problemi sono descritte oltre.

Prima di proseguire nella descrizione dei diversi schemi di raffreddamento finora dimostratisi validi è interessante studiare qual è il limite inferiore per la temperatura che ci si attende di poter raggiungere con questi metodi. Finora infatti si è discussa la possibilità di frenare un atomo. Per poter parlare di raffreddamento si deve considerare la possibilità di ridurre, in un campione di molti atomi, la larghezza della distribuzione delle loro velocità.

Un limite minimo fondamentale è costituito dalla temperatura T_r, detta temperatura di rinculo. Questo limite è dovuto al fatto che lo scambio di impulso tra atomi e radiazione laser avviene per quantità discrete; l'indeterminazione finale sulla velocità degli atomi non può quindi essere inferiore a quella corrispondente al rinculo per emissione di un singolo fotone:

[3] formula

con k_B costante di Boltzmann. Questo limite corrisponde a temperature estremamente basse. Per es., per la transizione D₂ dell'atomo di sodio si ha T_r52,4 ÌK; per il cesio T_r5197 nK. In realtà, nei processi di raffreddamento basati sulla diffusione di fotoni per emissione spontanea esiste un'altra temperatura limite, detta temperatura Doppler T_D. L'esistenza di questo limite è dovuta alla natura casuale del processo di emissione spontanea. Per un campione di atomi con un impulso ben definito, l'emissione spontanea di fotoni, essendo isotropa, non varia il valor medio KpL dell'impulso ma porta a un aumento della indeterminazione nei valori dell'impulso, ossia a un aumento della quantità Kp²L. Se si studia la competizione tra questo effetto e quello di raffreddamento laser si trova che la temperatura T_D è data dalla relazione:

[4] formula.

Questa temperatura è generalmente maggiore di T_r. Nel caso del sodio si ha T_D5240 ÌK; nel caso del cesio T_D5120 ÌK.

Nel seguito vengono descritti i metodi di raffreddamento laser che hanno permesso di raggiungere la temperatura Doppler T_D e di dimostrare la possibilità di scendere al di sotto di tale temperatura fino ad avvicinarsi alla temperatura di rinculo T_r.

Rallentamento di un fascio atomico

I primi esperimenti di raffreddamento di atomi mediante radiazione laser sono stati eseguiti su fasci collimati di atomi. Un esperimento di raffreddamento di atomi in un fascio atomico è in principio più semplice di quello di raffreddamento di atomi in un gas. Infatti, se il fascio è ben collimato, la dispersione delle velocità nelle direzioni perpendicolari a quella del moto degli atomi è già molto bassa, cosicché ci si può limitare a un esperimento di raffreddamento in una sola dimensione.

fig. 1

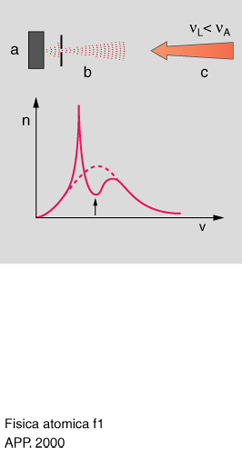
Come si è detto in precedenza, un fascio di atomi può essere rallentato inviando un fascio laser in direzione opposta a quella del moto degli atomi. La frequenza della radiazione laser deve essere tale da poter essere assorbita dagli atomi. A causa dell'effetto Doppler dovuto al moto degli atomi, la frequenza del laser deve essere accordata a una frequenza ν_L, minore della frequenza di risonanza atomica ν_A, che dipende dalla velocità v degli atomi che si vuole rallentare. Dalla [2] si vede che la forza su un atomo è piccola se [δ2ν_L(v/c)]@Γ, ossia se il disaccordo effettivo del laser è molto maggiore della larghezza naturale della riga atomica. Detto in altri termini, per ogni valore della frequenza del laser potranno risentire di una forza non trascurabile solo gli atomi in un intervallo di velocità di larghezza ¢v,Γc/ν_L, detto intervallo di cattura. Se, per es., si considera un fascio termico di atomi di sodio, si ha che l'intervallo di cattura è di 6 m/s, molto piccolo rispetto alla larghezza corrispondente alla distribuzione delle velocità atomiche nel fascio, che è di 500 m/s. La fig. 1 mostra infatti il cambiamento nella distribuzione delle velocità atomiche prodotto da un laser di frequenza ν_L,ν_A. Gli atomi la cui velocità iniziale è tale da interagire con il laser vengono rallentati fino a raggiungere una velocità al di fuori dell'intervallo di cattura. Gli atomi inizialmente al di fuori di questo intervallo non interagiscono con il laser e non vengono rallentati. Come si vede dalla fig., l'effetto del laser è di rallentare una parte degli atomi e di 'comprimere' le loro velocità accumulandoli in un intervallo di velocità minore di quello iniziale. Si ha quindi un effetto di raffreddamento oltre che di rallentamento degli atomi.

fig. 2

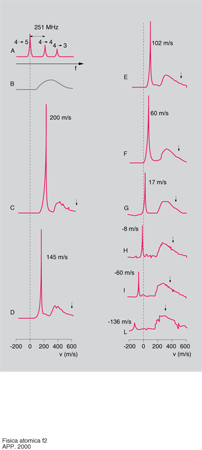
Il problema connesso a questo schema è che solo una piccola parte degli atomi viene rallentata e solo di una piccola quantità. Per risolvere questo problema si possono utilizzare due metodi: 1) si può variare la frequenza del laser in modo che alcuni atomi siano sempre in risonanza con il laser fino a raggiungere la velocità desiderata; 2) si può, utilizzando un campo magnetico esterno, variare la frequenza di risonanza atomica in modo che sia verificata la condizione di risonanza. Nel primo metodo, la frequenza del laser viene variata linearmente nel tempo. Il disaccordo della frequenza laser rispetto alla risonanza atomica varia quindi tra un valore δ_in e un valore δ_fin. Il valore di δ_in determina la velocità massima degli atomi che interagiscono con il laser; δ_fin fissa invece a quale velocità gli atomi vengono portati alla fine del processo di rallentamento. Se δ_fin,0, gli atomi vengono rallentati fino a v,0. Nella fig. 2 sono mostrate le distribuzioni di velocità atomiche ottenute in un fascio rallentato di cesio per diversi valori di δ_fin. Gli atomi vengono rallentati fino a velocità intorno allo zero ed è anche possibile invertirne la velocità.

Si noti che durante una 'spazzata' della frequenza del laser solo un gruppo di atomi viene rallentato. Gli atomi che escono dalla sorgente con una velocità più alta di quella corrispondente alla risonanza con il laser in quell'istante proseguono indisturbati e non vengono rallentati. Solo ripetendo il processo diverse volte e utilizzando un apparato sufficientemente lungo, è possibile rallentare una frazione elevata degli atomi nel fascio. Poiché il rallentamento di atomi veloci richiede uno spazio maggiore di quello necessario per il rallentamento di atomi inizialmente lenti, in questo schema gli atomi rallentati non sono localizzati ma distribuiti lungo il fascio. La necessità di variazioni comunque molto rapide della frequenza di emissione del laser può rappresentare un problema dal punto di vista sperimentale. L'applicazione di questo metodo di raffreddamento è stata molto semplificata dall'uso di laser a diodo semiconduttore, la cui frequenza di emissione può essere rapidamente variata agendo direttamente sulla corrente di iniezione.

fig. 3

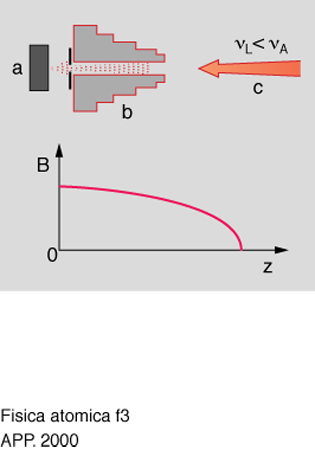
Un metodo diverso da quello fin qui esposto fa uso di un campo di induzione magnetica statico non omogeneo B(z) per avere una frequenza di risonanza atomica dipendente dalla posizione z degli atomi lungo il fascio atomico. Lo scopo è ancora di conservare, al variare della velocità degli atomi rallentati, la condizione di risonanza tra frequenza atomica e frequenza laser; in questo caso, però, si utilizza lo spostamento Zeeman dei livelli atomici per variare la frequenza atomica lasciando invece invariata la frequenza del laser. La differenza rispetto al metodo illustrato prima non è solo tecnica. Mentre lì, per diverse velocità atomiche, la risonanza veniva realizzata in diversi istanti della 'spazzata' della frequenza laser, qui si ha la risonanza in diverse zone del magnete. Mentre lì il parametro da ottimizzare era l'andamento temporale della frequenza laser, qui è l'andamento spaziale dell'intensità del campo magnetico. In fig. 3 è mostrato lo schema di un apparato per il frenamento di un fascio di atomi con questo metodo. Un solenoide a sezione variabile viene utilizzato per generare il campo magnetico. Nel caso di un fascio di sodio con v_in,1000 m/s, per es., l'intensità massima del campo magnetico richiesto è B₀,0,1 T. È necessario quindi usare solenoidi di notevoli dimensioni o elevati valori di corrente. Il maggior vantaggio offerto da questo metodo è che esso permette di rallentare e raffreddare una frazione anche molto elevata degli atomi del fascio, portandoli tutti alla stessa velocità all'uscita del solenoide.

Melasse ottiche

fig. 4

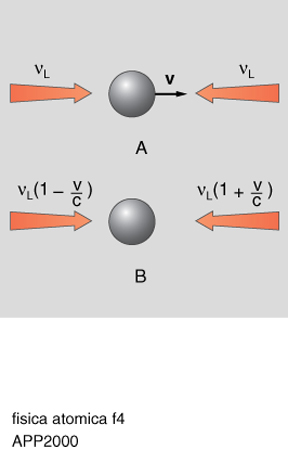
Nel paragrafo precedente si è descritto il frenamento di un fascio atomico con un fascio laser che si propaga in direzione opposta al moto degli atomi. In realtà la prima proposta di raffreddamento di atomi con radiazione laser, fatta da T.W. Hänsch e A.L. Schawlow nel 1975, prevedeva per il raffreddamento in una dimensione l'uso di due fasci laser di frequenza più bassa di quella di risonanza e con direzioni di propagazione opposte (fig. 4). In questo schema, se l'atomo si muove verso destra, a causa dell'effetto Doppler vede la frequenza del fascio che proviene da destra più vicina alla risonanza di quella del fascio che proviene da sinistra. Assorbirà quindi fotoni soprattutto dal fascio di destra e la sua velocità diminuirà. Allo stesso modo, se l'atomo si muove verso sinistra assorbirà fotoni dal fascio che proviene da sinistra e, anche in questo caso, la sua velocità diminuirà. L'atomo risente quindi di una forza in direzione sempre opposta a quella della sua velocità, una forza di tipo viscoso che ha suggerito, per questo schema, il nome di melassa ottica.

Infatti, utilizzando la [2] per questa configurazione in una dimensione, si può scrivere la forza esercitata dai due fasci laser sull'atomo come la somma delle forze esercitate da ognuno dei due fasci (questo è corretto se si può trascurare l'emissione indotta di fotoni, ossia se I/I₀!1). Si ha allora:

[5] formula.

La forza è sempre in direzione opposta alla velocità atomica. Per basse velocità (v,Γc/(2ν_L)) la forza dipende linearmente dalla velocità; infatti, per piccoli valori di v la [5] può essere approssimata con l'espressione:

[6] formula.

fig. 5

Si ha appunto una forza di tipo viscoso e α rappresenta il coefficiente di viscosità. Per un dato valore di I/I₀, il valore massimo di α si ottiene per 2δ/Γ521/√23. Il modello utilizzato fin qui è valido soltanto in una dimensione e nei limiti delle approssimazioni fatte. L'estensione a più dimensioni e a casi più generali è difficile. Dal punto di vista sperimentale una melassa in tre dimensioni è stata realizzata per la prima volta dal gruppo di S. Chu nel 1985 (fig. 5).

L' assorbimento e la riemissione di fotoni può avere due effetti: il primo è un raffreddamento degli atomi causato dalla forza viscosa ricavata sopra; il secondo effetto è invece un riscaldamento dovuto alla natura discreta e casuale dello scambio di impulso tra atomo e campo elettromagnetico. A seconda della temperatura, dominerà un processo o l'altro. La temperatura di equilibrio sarà quella per cui i due processi si bilanciano. Utilizzando la definizione di temperatura k_BT/25MKv²L/2, si ottiene

[7] formula.

La temperatura minima si ottiene per δ5Γ/2 e corrisponde alla temperatura limite Doppler T_D, data dalla [4]: k_BT_D5hΓ/2.

Sorprendentemente, misurazioni accurate della temperatura degli atomi raffreddati, effettuate in esperimenti condotti inizialmente da W. Phillips, hanno mostrato che è possibile raggiungere temperature molto più basse del limite Doppler. La misura della temperatura in una melassa atomica non è una misura semplice. Una possibilità sarebbe quella di misurare l'allargamento Doppler di una riga ma, date le bassissime velocità degli atomi, questo allargamento è molto piccolo. Esso è in genere inferiore alla larghezza naturale tipica delle righe atomiche a meno di utilizzare transizioni estremamente deboli. Il metodo più diffuso è quello della misura del tempo di transito degli atomi in una regione posta al di sotto della melassa.

fig. 6

fig. 7

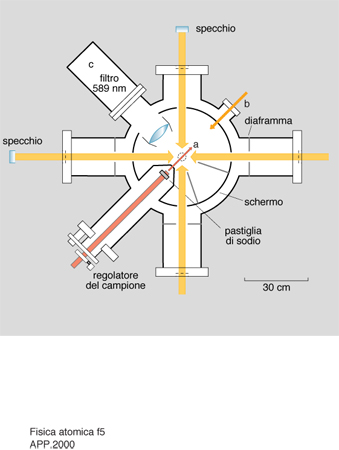
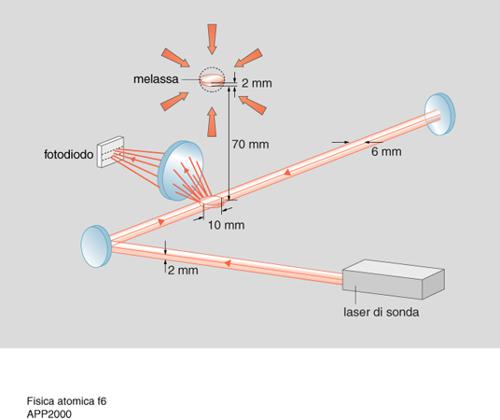
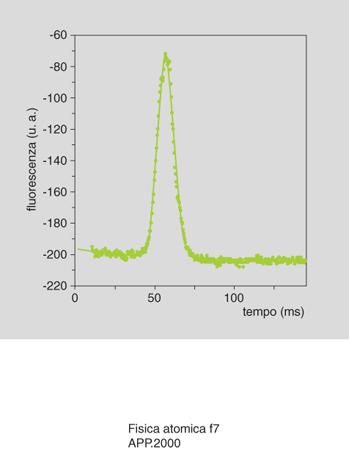
L'apparato è schematicamente mostrato in fig. 6. Dopo aver raffreddato gli atomi in una melassa, i fasci laser vengono spenti e gli atomi cadono per effetto della gravità. Al di sotto della melassa viene inviato un fascio laser di sonda la cui frequenza è risonante con la transizione atomica. Il passaggio degli atomi attraverso questo fascio viene rivelato misurando con un fotodiodo la luce da essi emessa per fluorescenza. Poiché gli atomi inizialmente più veloci raggiungono prima la regione di osservazione rispetto a quelli più lenti, dal tempo totale di transito degli atomi attraverso il fascio di sonda se ne può ricavare la distribuzione di velocità. La fig. 7 mostra infatti il risultato di un esperimento realizzato presso il laboratorio LENS (Laboratorio Europeo di Spettroscopia non Lineare) di Firenze con atomi di cesio. La temperatura che si ricava da questa misura è di 2,5 ÌK. Questa temperatura è più bassa di quella Doppler che è, come si è detto, di 120 ÌK.

Non solo le misure di temperatura, ma anche altre osservazioni sulle caratteristiche delle melasse ottiche di atomi alcalini hanno mostrato che il modello descritto prima per il raffreddamento Doppler fornisce previsioni in disaccordo con i risultati sperimentali. Per es., si trova che la temperatura minima raggiungibile sperimentalmente è proporzionale alla quantità I/δ.

fig. 8

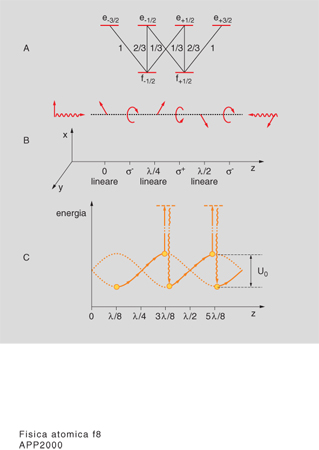
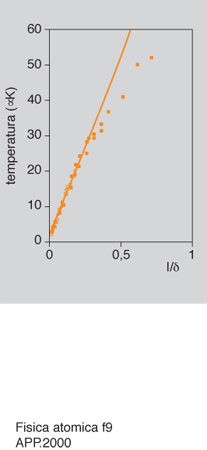
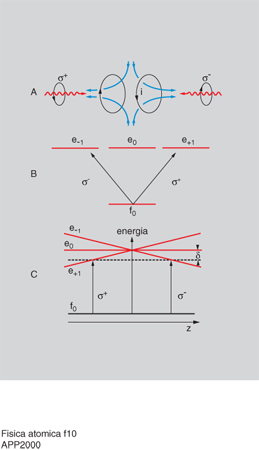
Per comprendere queste osservazioni, si deve considerare un atomo i cui livelli di energia presentano una struttura fatta di diversi sottolivelli Zeeman e tener conto di un effetto della radiazione elettromagnetica sui livelli atomici detto effetto Stark dinamico o spostamento luminoso dei livelli. Questo effetto consiste appunto nella variazione dei livelli di energia di un atomo dovuta alla presenza di radiazione di frequenza quasi risonante con una transizione che coinvolge quei livelli. Lo spostamento dei livelli dipende dalla quantità I/δ. Inoltre, per un dato sottolivello Zeeman, lo spostamento dipende dalla polarizzazione della radiazione ed è tanto maggiore quanto maggiore è la probabilità di eccitazione a partire da quel sottolivello. Se la polarizzazione della radiazione non è costante ma è diversa in diverse regioni dello spazio, lo spostamento dei livelli di energia dipenderà dalla posizione dell'atomo. In fig. 8 è mostrato il caso di due onde polarizzate linearmente che si propagano in direzioni opposte. Le due polarizzazioni sono perpendicolari tra di loro. Questa è una configurazione possibile per realizzare una melassa. Dalla fig. si vede che la polarizzazione del campo risultante varia a seconda della posizione; si hanno quindi dei gradienti di polarizzazione. La fig. mostra lo spostamento luminoso dei livelli nel caso δ,0 per un atomo che nello stato fondamentale ha momento angolare J_f51/2 (m_f561/2) e nello stato eccitato ha J_e53/2 (m_e561/2,63/2). Per δ,0, tutti i sottolivelli dello stato fondamentale sono spostati verso il basso; gli spostamenti sono, come si è detto, proporzionali alle probabilità di eccitazione che sono indicate, per i livelli considerati, in fig. 8A. Al variare della polarizzazione della radiazione la posizione dei livelli oscilla nello spazio. Osservando la fig. 8C. si può comprendere qual è il meccanismo che può portare al rallentamento dell'atomo se esso si muove in presenza delle due onde. Supponiamo che l'atomo si muova da sinistra verso destra a partire dalla posizione z5λ/8. A causa della polarizzazione σ⁻ della luce, l'atomo viene pompato otticamente nel sottolivello m_f521/2. Se l'atomo ha una velocità tale da percorrere una distanza dell'ordine di λ/4 nel tempo τ_p necessario per il pompaggio ottico da un sottolivello all'altro dello stato fondamentale, esso rimarrà nel sottolivello m_f521/2 fino a raggiungere una posizione in cui la polarizzazione della radiazione è σ⁺; potrà allora effettuare la transizione verso il livello m_e511/2 dello stato eccitato e decadere poi nel sottolivello m_f511/2, a partire dal quale può effettuare un altro ciclo. In questo processo di pompaggio ottico da un sottolivello all'altro, l'atomo ha perso una energia cinetica pari alla separazione tra i due sottolivelli nella zona di eccitazione. Come si è detto, questa separazione è proporzionale a I/δ. Questo effetto è stato chiamato effetto Sisifo da C. Cohen-Tannoudji e J. Dalibard che sono stati i primi a spiegare in questo modo le basse temperature osservate nelle melasse; come nel mito di Sisifo, infatti, l'atomo è costretto a 'scalare' continuamente barriere di potenziale da cui poi cade. Si può comprendere quindi come questo effetto possa portare a un raffreddamento degli atomi e anche, poiché in ogni ciclo un atomo perde una quantità di energia dell'ordine di U₀, perché il limite alla temperatura minima raggiungibile sia proprio dato da questa quantità. Si ha quindi:

[8] formula.

fig. 9

Ci si attendono dunque temperature tanto più basse quanto più bassa è l'intensità del laser e quanto maggiore è il disaccordo δ. Questo andamento è stato verificato sperimentalmente in melasse tridimensionali fino a temperature molto basse (fig. 9). Il limite inferiore è dato dall'effetto di riscaldamento dovuto alla diffusione dei fotoni, che diventa importante quando U₀ è confrontabile con l'energia di rinculo. Nel caso del sodio la minima temperatura ottenuta è stata di 20 ÌK corrispondente a ,8 T_r. Nel caso del cesio il limite minimo misurato è stato di 2,5 ÌK, pari a ,12 T_r.

È bene osservare che la descrizione fatta fin qui dei processi di interazione tra gli atomi e la radiazione laser è di tipo semiclassico. Infatti, l'atomo viene considerato come una particella puntiforme con valori ben determinati di posizione e velocità. Questa approssimazione è valida solo se la dimensione del pacchetto d'onda associato all'atomo è molto minore della lunghezza d'onda della radiazione e se l'indeterminazione sulla velocità è tale che la larghezza Doppler è minore della larghezza naturale della risonanza. Quando però la temperatura si avvicina alla temperatura di rinculo, la lunghezza d'onda di de Broglie dell'atomo diventa dell'ordine della lunghezza d'onda della radiazione e l'approssimazione semiclassica non è più corretta. Per la descrizione del sistema atomi-radiazione in queste condizioni è allora necessaria una trattazione puramente quantistica. Esistono attualmente due diversi metodi di raffreddamento laser che hanno permesso di raggiungere temperature dell'ordine o più basse di quella di rinculo, che per brevità vengono solo citati.Il primo è detto intrappolamento coerente e selettivo in velocità di popolazione atomica (VSCPT, dall'ingl. Velocity Selective Coherent Population Trapping) ed è basato sull'effetto di intrappolamento degli atomi in uno stato in cui non possono assorbire luce, effetto scoperto nel 1976 da A.Gozzini a Pisa. Il secondo metodo è detto raffreddamento Raman in quanto è basato su transizioni Raman selettive in velocità che portano gli atomi a velocità vicine a v50.

La trappola magneto-ottica

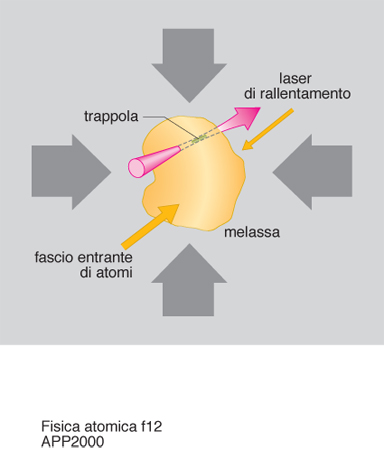
La trappola magneto-ottica (spesso chiamata MOT, dall'ingl. Magneto-Optical Trap) è quella attualmente più usata per l'intrappolamento di atomi neutri. Essa è relativamente semplice da realizzare e permette di intrappolare e raffreddare molti atomi con elevate densità anche a partire da un gas a temperatura ambiente. Una trappola magneto-ottica consiste essenzialmente nella combinazione di una configurazione di fasci laser analoga a quella usata per una melassa e di un campo magnetico statico disomogeneo.

fig. 10

Il principio di funzionamento può essere compreso considerando il modello semplice in una dimensione illustrato in fig. 10. Due fasci laser contropropaganti, polarizzati circolarmente in versi opposti, interagiscono con un atomo in presenza del campo magnetico disomogeneo. Per semplicità, l'atomo viene considerato con soli due livelli, uno fondamentale e uno eccitato, di momento angolare J_f50 e J_e51. Il campo magnetico è nullo al centro, è diretto verso destra a destra del centro e verso sinistra a sinistra, come mostrato in fig. 10A. A causa dell'effetto Zeeman, il campo magnetico provoca una separazione dei sottolivelli magnetici m_e521, 0, 11. Per la regola di selezione che deriva dalla conservazione della proiezione J_z del momento angolare lungo l'asse z, si ha che il fascio polarizzato σ⁻ che proviene da destra può indurre solo la transizione verso il livello m_e521, mentre il fascio polarizzato σ⁺ che proviene da sinistra può eccitare solo la transizione verso il livello m_e511. Se i fasci laser hanno una frequenza minore di quella della transizione atomica si ha che un atomo che si trova a destra del centro della trappola a causa dell'effetto Zeeman interagisce maggiormente con il fascio che proviene da destra effettuando la transizione m_f50¢m_e521. La pressione di radiazione spinge allora l'atomo verso il centro. Allo stesso modo un atomo che si trovi a sinistra del centro della trappola viene spinto verso il centro dal fascio che proviene da sinistra.

Una caratteristica importante della trappola magneto-ottica è che in essa gli atomi non solo vengono intrappolati ma anche raffreddati. Il meccanismo di raffreddamento è analogo a quello che si ha in una melassa (si è trovato che anche nella trappola magneto-ottica si può avere un raffreddamento sub-Doppler dovuto al gradiente di polarizzazione). Rispetto a una melassa, però, la presenza del campo magnetico ha un effetto analogo a quello descritto per il raffreddamento di un fascio atomico.

La forza risentita dagli atomi in una trappola magneto-ottica può essere scritta come la somma delle forze esercitate da ognuno dei due fasci laser. Si ha allora un'espressione analoga alla [5] trovata per le melasse ottiche; in questo caso, però, nell'espressione del disaccordo effettivo d_eff va incluso lo spostamento dei livelli atomici, prodotto dal campo magnetico, dato da (μ_B/h)B(z)(g_em_e2g_fm_f), dove μ_B è il magnetone di Bohr, g_e e g_f rappresentano i fattori di Landé dei due livelli. Per piccole distanze z dal centro della trappola, si può considerare che il campo vari linearmente con la distanza, ossia B(z)5B₀z. Assumendo anche per semplicità (g_em_e2g_fm_f),1, lo spostamento dei livelli prodotto dal campo magnetico può essere scritto come (μ_B/h)B₀z5βz. Nel limite di bassa velocità e di debole campo magnetico, la forza F(v, z) esercitata su un atomo con velocità v nella posizione z può essere scritta come:

[9] formula

Rispetto all'espressione [6] trovata nel caso delle melasse, si ha quindi una dipendenza della forza dalla posizione z dell'atomo. Il moto dell'atomo per effetto di questa forza è quindi un moto armonico smorzato.

Grazie all'efficienza del processo di raffreddamento, la profondità effettiva di questa trappola, ossia la temperatura massima degli atomi che possono esservi intrappolati, è maggiore di quella statica, che è tipicamente dell'ordine di qualche K.

fig. 11

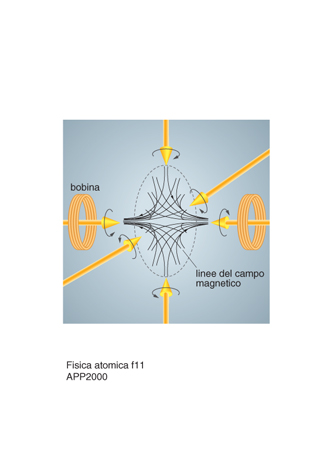
Lo schema descritto nel caso di una sola dimensione può essere esteso all'intrappolamento in tre dimensioni utilizzando tre coppie di fasci contropropaganti polarizzati circolarmente che si intersecano nella zona dove il campo magnetico è nullo, come mostrato in fig. 11. La fig. mostra anche come viene generato il campo magnetico della forma richiesta per l'intrappolamento in tre dimensioni utilizzando due bobine in configurazione 'anti-Helmholtz', ossia due bobine parallele percorse dalla stessa corrente i, come nelle bobine di Helmholtz, ma in versi opposti.

La trappola magneto-ottica rappresenta un sistema molto efficace per la raccolta e il raffreddamento di atomi a partire da fasci atomici o anche da un gas in una cella a temperatura ambiente. Sono state finora intrappolate diverse specie atomiche che presentano transizioni adatte di lunghezza d'onda raggiungibile dai laser disponibili, quali atomi di metalli alcalini, alcalino-terrosi o di gas nobili in livelli metastabili. Il numero degli atomi intrappolati e le densità atomiche ottenibili sono notevoli. In una trappola magneto-ottica di cesio, per es., si possono tipicamente intrappolare 10⁸ atomi in un volume di circa 1 mm³, con densità quindi di 10¹⁰410¹¹ atomi/cm³, a temperature di 504100 ÌK. Gli atomi intrappolati possono essere 'visti' osservando la luce che essi emettono per fluorescenza.

Data la sua versatilità, in molti esperimenti la trappola magneto-ottica viene utilizzata come primo stadio per la raccolta di un numero elevato di atomi a bassa temperatura; interrompendo poi la corrente nelle bobine e lasciando i fasci laser accesi, si può ottenere una melassa atomica. Si possono avere in questo modo elevate densità di atomi alle temperature estremamente basse raggiungibili in una melassa.

La trappola dipolare

La trappola dipolare è una trappola puramente ottica. Essa è basata sulla forza dipolare, proporzionale al gradiente d'intensità della radiazione. L'origine di questa forza può essere compresa considerando l'atomo in presenza della radiazione elettromagnetica come un oscillatore armonico carico forzato. Il momento di dipolo oscillante d è in fase con il campo elettromagnetico E se la frequenza della radiazione è minore di quella di risonanza, mentre è in opposizione di fase per frequenze maggiori della risonanza. L'energia di interazione tra il dipolo e il campo è W52d?E. Per frequenze minori di quella di risonanza, l'energia W è negativa e quindi, se l'intensità non è costante, l'oscillatore è attirato verso la regione di massima intensità.

La forza dipolare può anche essere interpretata come dovuta all'effetto Stark dinamico. Infatti, come già si è detto in precedenza, la radiazione elettromagnetica provoca uno spostamento dei livelli atomici che, con buona approssimazione, è proporzionale all'intensità I della radiazione e inversamente proporzionale alla differenza δ tra la sua frequenza e la frequenza di risonanza atomica. In presenza di un gradiente di intensità, un atomo risente quindi di una forza che può essere derivata da un potenziale U proporzionale alla quantità I/δ.

fig. 12

Una trappola dipolare può essere realizzata focalizzando un fascio laser gaussiano di frequenza minore di quella di risonanza (fig. 12). Un atomo nella regione del fuoco si trova allora nel massimo di intensità e può rimanervi intrappolato. In questa trappola non si ha diminuzione di energia e quindi non si ha alcun effetto di raffreddamento degli atomi. Per intrappolare gli atomi è necessario che essi siano stati già raffreddati (per es., in una melassa) a temperature inferiori alla profondità della trappola (tipicamente dell'ordine di qualche frazione di K). Un'altra condizione importante è che il riscaldamento dovuto all'assorbimento e riemissione spontanea di fotoni non provochi un aumento troppo rapido della temperatura degli atomi, espellendoli dalla trappola. Dalla espressione [1] si vede che, per valori sufficientemente grandi del disaccordo δ, il numero di fotoni emessi spontaneamente da un atomo in un dato tempo è proporzionale alla quantità I/δ². Per ottenere lunghi tempi di intrappolamento è necessario quindi utilizzare il più grande valore di disaccordo δ possibile, compatibilmente con l'intensità laser disponibile. In questo modo, a parità di profondità della trappola, viene ridotto il tasso di emissioni spontanee e quindi il riscaldamento degli atomi.

Sebbene la trappola dipolare sia concettualmente molto semplice, la sua realizzazione pratica presenta dei problemi connessi, appunto, alla necessità di elevate potenze laser. Essa offre d'altra parte dei vantaggi importanti rispetto ad altre trappole in quegli esperimenti in cui è necessario che gli atomi, oltre a essere confinati con elevate densità e in un volume molto piccolo, si trovino tutti nel livello fondamentale. Inoltre, poiché questa trappola non richiede l'assorbimento di fotoni, essa può essere estesa all'intrappolamento di sistemi con spettri di assorbimento molto più complessi di quelli atomici, quali molecole o microparticelle molto lente.

Condensazione di Bose-Einstein

La condensazione di Bose-Einstein (BEC, Bose-Einstein Condensation) è un fenomeno puramente quantistico, per cui un gas di particelle identiche non interagenti, descritto da una funzione d'onda simmetrica per lo scambio di due di esse, dovrebbe subire una transizione di fase quando la lunghezza d'onda di de Broglie diventa confrontabile con la distanza tra le particelle. Come è noto, nella teoria quantistica le particelle descritte da una funzione d'onda simmetrica per lo scambio di due particelle sono dette bosoni e obbediscono alla statistica di Bose-Einstein. Le particelle descritte da una funzione d'onda antisimmetrica sono invece dette fermioni e obbediscono alla statistica di Fermi-Dirac. Quando la temperatura di un gas di bosoni è ridotta al di sotto di un valore critico, ci si attende che essi si accumulino nel livello fondamentale del sistema evidenziando aspetti di comportamento collettivo analogo a quello che si ha nella superfluidità dell'elio. Tale transizione avviene per densità nello spazio delle fasi nΛ³_dB=2.612 (che corrisponde alla cosiddetta condizione di degenerazione quantistica) dove n è la densità delle particelle e Λ_dB è la lunghezza d'onda di de Broglie. Quest'ultima dipende dalla massa m delle particelle e dalla temperatura termodinamica T tramite la relazione Λ_dB=h/(2πmk_BT)¹^/².

Come già detto, l'osservazione diretta della condensazione di Bose-Einstein è stata riportata solo nel 1995 da E.A. Cornell e collaboratori, del laboratorio JILA (Joint Institute for Laboratory Astrophysics), con atomi di rubidio (⁸⁷Rb). Subito dopo è stata osservata dal gruppo di W. Ketterle, del MIT, con atomi di sodio (²³Na). Il regime di degenerazione quantistica è stato raggiunto anche per gli atomi di litio (⁷Li) e idrogeno. Le ragioni di tanta attesa tra predizione e osservazione sperimentale sono da ricercarsi nel fatto che la condizione di degenerazione quantistica richiede di operare ad alte densità e a temperature bassissime. Nel caso dell'atomo di rubidio, per raggiungere la condensazione di Bose-Einstein è necessario raffreddare un gas di atomi con densità di ∼10¹³/cm³ a una temperatura di circa 150 nK. È evidente che in questo caso non possono essere utilizzati metodi convenzionali di refrigerazione anche perché bisogna evitare che al diminuire della temperatura il gas prima si liquefaccia e poi solidifichi. Gli esperimenti sono stati quindi condotti sotto alto vuoto e hanno utilizzato l'interazione degli atomi con la radiazione laser per il raggiungimento di temperature dell'ordine dei μK. Queste temperature non sono ancora sufficientemente basse per la transizione di fase, ma consentono di catturare gli atomi in trappole magnetiche e di raffreddarli ulteriormente mediante un processo di 'evaporazione'.

Lo studio di questi fenomeni su atomi raffreddati e intrappolati presenta diversi vantaggi rispetto ad altri sistemi in cui è possibile evidenziare effetti di questo tipo. Un aspetto importante deriva dal fatto che si parte da atomi poco interagenti e in assenza di perturbazioni esterne. Inoltre, essendo possibile variare la temperatura e la densità degli atomi, si può studiare la transizione tra le due fasi in diverse condizioni. Questa circostanza permette una semplificazione dei processi e una loro comprensione più profonda.

Il metodo utilizzato per raggiungere le densità e le temperature richieste per il verificarsi della condensazione di Bose-Einstein è basato sulla successione di tre fasi: 1) raffreddamento e confinamento degli atomi mediante radiazione laser; 2) confinamento degli atomi in una trappola magnetica; 3) ulteriore raffreddamento e compressione degli atomi nella trappola mediante 'evaporazione'.

Intrappolamento magnetico

fig. 13

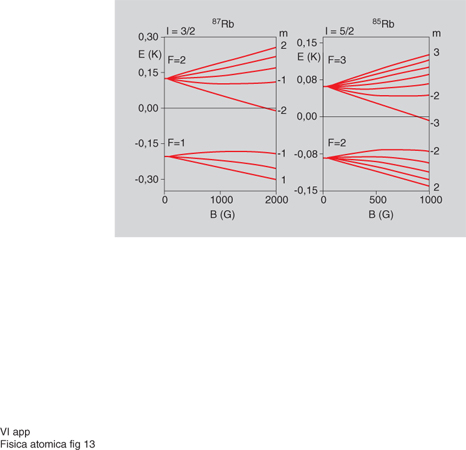
Le trappole magnetiche sono realizzate mediante un campo magnetico disomogeneo con un minimo locale. Gli atomi dotati di un momento magnetico μ in un campo di induzione magnetica B hanno energia W=−μ∙B e risentono di una forza F=grad(μ∙B), la cui direzione dipende dall'orientazione del momento magnetico rispetto alla direzione del campo. Se il moto atomico può essere considerato adiabatico (ossia l'atomo resta nello stesso sottolivello Zeeman durante il moto), esso può essere descritto con un potenziale dato localmente dal momento magnetico moltiplicato B. In presenza di un minimo di B, gli atomi che si trovano in uno stato la cui energia aumenta all'aumentare del campo magnetico risentono di una forza di richiamo verso la regione di minimo e possono essere intrappolati. La fig. 13 mostra, per es., l'energia E in kayser (1 kayser≃1,24∙10⁻⁴ eV) dei sottolivelli Zeeman dello stato fondamentale dell'atomo di ⁸⁷Rb e ⁸⁵Rb in funzione dell'induzione magnetica B (in gauss). Gli atomi di ⁸⁷Rb quindi possono essere intrappolati negli stati ∣F=1, m=−1> e ∣F=2, m=1, 2>; gli atomi di ⁸⁵Rb invece possono essere intrappolati negli stati ∣F=2, m=−1,−2> e ∣F=3, m=1, 2, 3>. Una trappola magnetica fu usata per la prima volta da W. Paul per confinare neutroni. L'intrappolamento magnetico di atomi fu dimostrato all'inizio su atomi di sodio e successivamente è stato utilizzato per diversi atomi quali H, Li, K, Rb, Cs, Eu.

Se confrontate con le trappole magneto-ottiche, le trappole magnetiche permettono il confinamento degli atomi a temperature molto più basse perché sono assenti gli effetti di riscaldamento prodotti dalla luce (per es., l'effetto del rinculo). Le trappole magnetiche sono però molto meno 'profonde' delle MOT. La profondità tipica è dell'ordine di 1÷10 mK. È quindi chiaro che per confinare in una trappola magnetica atomi da un fascio atomico o da un vapore a temperatura ambiente, essi devono essere pre-raffreddati. Si deve tener presente che, poiché le trappole magnetiche sono trappole conservative, è necessario un meccanismo indipendente per raffreddare gli atomi nella trappola. Come discusso nel seguito, i metodi finora dimostrati sono quello detto del raffreddamento evaporativo e il raffreddamento mediante collisioni con un altro gas di atomi a bassa temperatura.

fig.

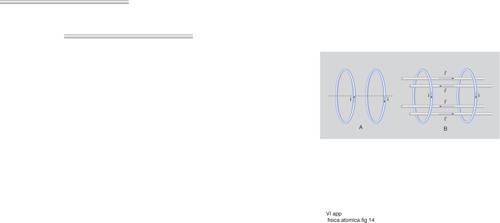
Lo schema più semplice per realizzare una trappola magnetica è la configurazione anti-Helmholtz mostrata in fig. 14 (A). Questa configurazione produce un campo quadrupolare sferico che è nullo al centro e varia linearmente in prossimità del centro stesso. Questo tipo di trappola fu usato negli esperimenti iniziali di confinamento di atomi. Oltre alla semplicità costruttiva, esso presenta il vantaggio di un forte confinamento degli atomi rispetto ad altri schemi, in cui il potenziale è di forma parabolica (v. oltre). Un difetto di questa trappola diventa evidente, tuttavia, quando gli atomi in essa confinati raggiungono temperature molto basse. Gli atomi possono sfuggire dalla trappola a causa di un processo detto spin-flip di Majorana. Infatti, gli atomi che si muovono in una trappola magnetica risentono di un campo magnetico la cui direzione varia continuamente. Perché essi restino intrappolati, i momenti magnetici atomici devono essere orientati in modo che essi siano attratti verso la regione di minimo del campo. Se il campo magnetico varia lentamente, il momento magnetico precede intorno alla direzione del campo e la segue adiabaticamente. La condizione di adiabaticità non è soddisfatta se la frequenza di precessione è piccola rispetto alla velocità di variazione della direzione del campo. La probabilità di una transizione non adiabatica tra due stati di spin per un fascio di atomi orientati che attraversano una regione in cui il campo magnetico si annulla fu calcolata da E. Majorana. Questo è quanto avviene nel caso di atomi che passano in prossimità del centro di una trappola quadrupolare. La perdita di atomi dalla trappola aumenta al diminuire della temperatura poiché gli atomi si trovano più vicini al centro della trappola dove il campo si annulla.

Per ridurre la perdita di atomi dovuta agli spin-flip sono stati messi a punto diversi metodi che permettono di confinare gli atomi in una regione in cui il campo ha un minimo ma non si annulla. Gli schemi utilizzati sono essenzialmente tre: 1) Nell'esperimento in cui la condensazione di Bose-Einstein fu osservata per la prima volta, venne utilizzata una trappola magnetica, detta trappola TOP (Time-averaged Orbiting Potential). Questa venne realizzata aggiungendo al campo magnetico quadrupolare, prodotto da due bobine orizzontali in configurazione anti-Helmholtz, un debole campo magnetico rotante velocemente nel piano orizzontale. Il moto degli atomi è allora determinato da un potenziale effettivo, dato dalla media temporale del potenziale istantaneo, che risulta essere di forma parabolica. Con un'opportuna scelta dei parametri, si può far sì che la regione in cui il campo si annulla si trovi all'esterno della regione di confinamento degli atomi. 2) Un altro metodo utilizzato inizialmente per ridurre le perdite dovute agli spin-flip di Majorana è detto optical-plug trap (trappola con 'tappo ottico'). Se il centro di una trappola quadrupolare viene considerato come un buco da cui gli atomi vengono persi, l'idea della trappola con optical-plug è di utilizzare la forza di dipolo prodotta da un fascio laser per allontanare gli atomi da questa regione, otturando quindi il buco. Questa trappola è stata realizzata facendo passare al centro della trappola un fascio laser focalizzato di frequenza maggiore di quella della risonanza atomica. 3) Lo schema attualmente più utilizzato, con diverse varianti, è detto trappola di Ioffe-Pritchard (fig. 14B). Esso deriva da uno schema utilizzato inizialmente per il confinamento di plasmi ed era stato tra i primi a essere suggerito per l'intrappolamento di atomi. Può essere realizzato con due bobine parallele percorse da corrente nello stesso verso, che producono un campo 'a forma di bottiglia' per il confinamento longitudinale, e quattro conduttori rettilinei con correnti in direzioni alternate, che producono il campo per il confinamento trasversale. Di questa trappola sono state messe a punto diverse varianti quali la trappola detta baseball, per la forma delle bobine che rassomiglia alle strisce su una palla da baseball, quella a quadrifoglio, di nuovo per la forma delle bobine che producono il campo, o con magneti permanenti.

Raffreddamento evaporativo degli atomi intrappolati

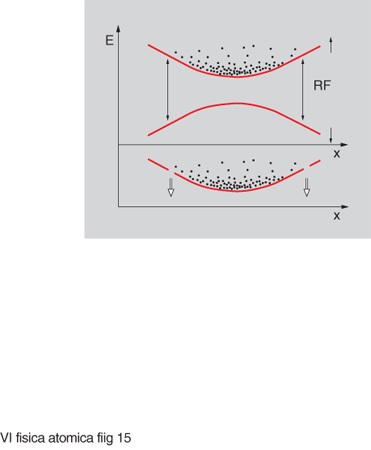
Il raffreddamento evaporativo di un gas di atomi intrappolati è basato sull'eliminazione selettiva degli atomi che hanno un'energia maggiore dell'energia media per atomo e sulla ritermalizzazione del campione dovuta alle collisioni. Poiché l'energia media degli atomi che restano nella trappola viene ridotta in questo processo, il nuovo stato di equilibrio del gas corrisponde a una temperatura più bassa. Con una procedura di evaporazione ben ottimizzata è possibile ottenere una notevole riduzione della temperatura e, ciò che è più importante negli esperimenti sulla condensazione di Bose-Einstein, un aumento della densità nello spazio delle fasi di diversi ordini di grandezza. Il metodo di raffreddamento per evaporazione fu inizialmente proposto e utilizzato per cercare di ottenere la condensazione di Bose-Einstein in un gas di idrogeno atomico. La tecnica fu poi estesa agli atomi alcalini e, in combinazione con il raffreddamento con luce laser, ha giocato un ruolo fondamentale nei recenti esperimenti in cui la condensazione è stata osservata.

fig. 15

Sono stati dimostrati diversi metodi per realizzare il raffreddamento evaporativo. Negli esperimenti di condensazione di atomi alcalini è stato utilizzato un metodo detto di evaporazione indotta da radiofrequenza. L'evaporazione forzata è stata ottenuta inducendo negli atomi delle transizioni di spin-flip, verso stati non intrappolati, mediante un campo a radiofrequenza (fig. 15). Poiché gli atomi con energia maggiore raggiungono zone della trappola dove il campo magnetico è maggiore, le frequenze corrispondenti alle transizioni di spin-flip sono più spostate a causa dell'effetto Zeeman. Per transizioni tra sottolivelli magnetici m_F, la condizione di risonanza è hν_rf=gμ_BB. Poiché il potenziale di intrappolamento è dato da m_Fgμ_B(B(r)−B(0)), gli atomi eliminati dalla trappola saranno quelli con energia E∼hm_F(ν_rf−ν₀) dove ν₀ è la frequenza corrispondente alla transizione di spin-flip al centro della trappola. Variando la frequenza del campo a radiofrequenza è quindi possibile eliminare dalla trappola atomi con un determinato valore di energia cinetica. Riducendo poi in maniera continua tale frequenza si possono ottenere progressivamente temperature più basse e densità più alte per gli atomi che restano nella trappola. Come già detto, un ruolo importante in questo processo viene giocato dalle collisioni elastiche nel gas che permettono la ritermalizzazione della distribuzione delle velocità atomiche modificata dalla evaporazione forzata. Perché il raffreddamento evaporativo funzioni è quindi necessaria una ottimizzazione del processo: infatti, se l'evaporazione indotta dalla radiofrequenza è troppo rapida rispetto alla velocità di ritermalizzazione del campione, si ottiene una distribuzione modificata a cui può non corrispondere un aumento della densità nello spazio delle fasi. Se, al contrario, l'evaporazione procede troppo lentamente, altri meccanismi come collisioni con il gas di fondo, collisioni anelastiche o spin-flip di Majorana possono portare a una perdita di atomi dalla trappola e quindi, di nuovo, a una bassa efficienza del processo di raffreddamento.

Il successo di un esperimento di raffreddamento evaporativo dipende quindi dal tasso di collisioni elastiche tra gli atomi intrappolati rispetto a quello delle collisioni anelastiche o con il gas di fondo nell'apparato.

Esperimenti sulla condensazione di Bose-Einstein

Nei paragrafi precedenti sono stati descritti quelli che sono gli 'ingredienti' fondamentali degli esperimenti in cui è stata raggiunta la condensazione di Bose-Einstein in un gas di atomi alcalini. Una volta raggiunte le condizioni per la condensazione, è necessario utilizzare un opportuno metodo di rivelazione per osservare il campione.

L'osservazione degli atomi nello stato condensato non è facile. Negli esperimenti effettuati finora le dimensioni del condensato sono solo di alcuni μm. È quindi difficile raggiungere una risoluzione sufficiente a osservare la distribuzione spaziale degli atomi nella trappola. Inoltre l'elevata densità ottica del campione fa sì che un fascio laser di frequenza risonante venga completamente assorbito, impedendo quindi l'osservazione del condensato.

fig. 16

fig. 17

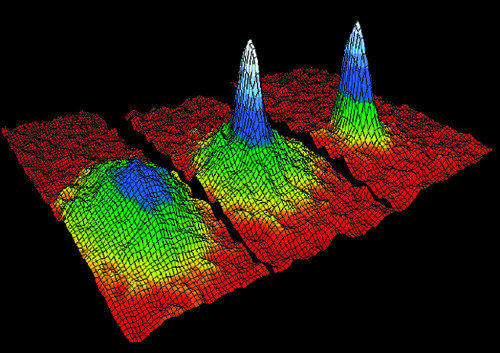
Nella maggior parte degli esperimenti finora effettuati, l'osservazione è stata fatta nel modo seguente: una volta conclusa la fase di raffreddamento evaporativo, viene spento il campo magnetico e si lascia espandere gli atomi. Dopo un tempo di alcune decine di ms, le dimensioni del campione sono tali da permetterne l'osservazione con una sufficiente risoluzione spaziale. Viene allora inviato sul campione un fascio laser di frequenza risonante con quella della transizione atomica e l'immagine dell''ombra' dovuta alla diffusione della luce da parte degli atomi viene osservata con una telecamera a CCD (Charge Coupled Device) (fig. 16). Questo metodo di osservazione è analogo a una misura di tempo di volo. L'immagine che si ottiene dà la proiezione della distribuzione di velocità iniziale degli atomi. D'altra parte in un potenziale armonico la distribuzione spaziale è identica alla distribuzione di velocità. Da una singola immagine si può quindi ottenere sia la distribuzione di velocità sia la distribuzione spaziale degli atomi e quindi misurarne quantità importanti quali la temperatura e la densità. In fig. 17 è mostrata l'immagine in falsi colori ottenuta per diverse condizioni di temperatura e densità. La parte a) mostra l'immagine ottenuta a una temperatura superiore a quella critica; la distribuzione di velocità è isotropa come ci si aspetta per un campione all'equilibrio termico. La parte b) corrisponde a una temperatura di poco inferiore a quella critica; si può quindi osservare una zona più densa di forma ellittica nella parte centrale. Questa forma ellittica è uno degli aspetti interessanti del fenomeno. Essa dipende dall'anisotropia del potenziale che confina gli atomi nella trappola (la costante di richiamo nella trappola è diversa per la direzione assiale e per quella radiale); tale anisotropia si riflette nell'asimmetria della funzione d'onda che descrive gli atomi nello stato condensato. Nella parte c) la temperatura è stata ridotta fino a ottenere un puro condensato.

È importante notare che questo metodo di osservazione distrugge il campione e per effettuare più misure è necessario ripetere tutto il processo di intrappolamento e raffreddamento. È stata però studiata anche la possibilità di una rivelazione di tipo non distruttivo. Si può infatti utilizzare l'effetto dispersivo che si ha se sul campione viene inviato un fascio laser di frequenza disaccordata rispetto alla risonanza. Il condensato agisce allora come una lente deflettendo la luce. Si può così, con opportuni accorgimenti, ottenere una chiara immagine del campione. Poiché la probabilità di assorbimento di fotoni da parte degli atomi diminuisce fortemente allontanandosi dalla frequenza di risonanza, questo metodo permette di osservare diverse volte lo stesso campione senza perturbarlo in maniera significativa. Questo può essere quindi considerato un metodo di osservazione non-distruttivo. In realtà, sebbene la diffusione di fotoni in maniera dispersiva non riscaldi il campione e non distrugga il condensato, a causa dell'effetto di spostamento luminoso dei livelli, verrà comunque modificata la fase del condensato. Un'altra possibilità per una osservazione di tipo non-distruttivo è offerta dal fatto che, essendo il campione polarizzato, esso cambierà lo stato di polarizzazione di un fascio luminoso polarizzato linearmente che lo attraversi. La rivelazione può essere fatta quindi in maniera analoga a quanto si fa, per esempio, nelle tecniche di spettroscopia in polarizzazione.

Sebbene la condensazione di Bose-Einstein sia stata osservata solo recentemente, nei laboratori in cui essa è stata ottenuta sono stati già condotti diversi esperimenti al fine di studiare le proprietà di quello che, per molti aspetti, può essere considerato un nuovo stato della materia. Per brevità, non è possibile in questa sede descrivere in dettaglio tali esperimenti ma ci si limita a descriverne sinteticamente le idee di base, dividendoli in tre temi principali: proprietà statiche, proprietà dinamiche, studio delle proprietà di coerenza e realizzazione di un 'laser atomico'.

fig. 18

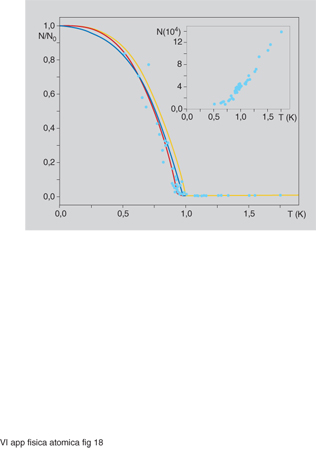
Proprietà statiche. - È stata misurata la frazione N/N₀ di atomi nel condensato in funzione della temperatura T (fig. 18). L'andamento trovato è in accordo con quello previsto teoricamente dal gruppo di S. Stringari a Trento. Anche per la temperatura critica, il valore misurato è in accordo con quello calcolato entro gli errori sperimentali; finora non è stata evidenziata alcuna differenza significativa dovuta alla interazione tra gli atomi. La dipendenza dell'energia dalla temperatura mostra una variazione della pendenza in corrispondenza della temperatura di transizione che indica una discontinuità nel calore specifico.

Proprietà dinamiche. - Modulando il potenziale di intrappolamento, sono state osservate eccitazioni di tipo fononico del condensato. Sono stati studiati i modi più bassi con differenti valori del momento angolare e dell'energia e se ne è analizzata la dipendenza dall'energia di interazione. Queste eccitazioni collettive sono state studiate anche al variare della temperatura e sono stati osservati modi collettivi analoghi al primo e secondo suono nell'elio liquido. Osservando la propagazione di una perturbazione nella densità, si è potuta misurare la velocità del suono.

fig. 19

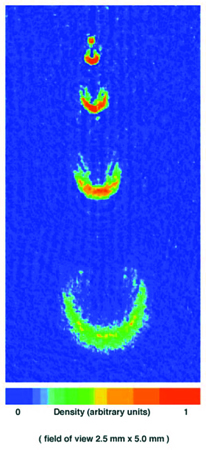
Proprietà di coerenza e 'laser atomico'. - In alcuni esperimenti recenti sono state studiate le proprietà di coerenza di un condensato di Bose-Einstein. Questo infatti può essere descritto da una funzione d'onda macroscopica alla quale può essere associata una fase. L'osservazione dell'interferenza tra due condensati indipendenti ha fornito la prova sperimentale della coerenza di un condensato. Infatti, un esperimento di interferenza tra due condensati separati può essere considerato analogo a un esperimento di interferenza da doppia fenditura in ottica. Oltre alla coerenza al primo ordine, gli esperimenti hanno evidenziato anche una coerenza al secondo e terzo ordine in un condensato. In questo ambito, una delle prospettive più interessanti è la realizzazione di un laser atomico ossia di una sorgente di un fascio atomico coerente. Finora è stato realizzato un sistema in cui atomi vengono emessi 'a pacchetti' da un condensato conservando le proprietà di coerenza (fig. 19). Questo può quindi essere considerato l'analogo di un laser funzionante in regime impulsato.

Oltre agli esperimenti sopra elencati, diversi altri esperimenti che coinvolgono atomi nello stato condensato sono stati già realizzati o sono in corso. Tra questi: a) lo studio della condensazione di Bose-Einstein per atomi con interazioni di tipo attrattivo; per l'atomo di litio la lunghezza di scattering in onda s è negativa, il che corrisponde, nelle collisioni tra atomi lenti, a una interazione di tipo attrattivo. È quindi interessante studiare per quali condizioni si riesce a ottenere un condensato stabile. b) Produzione di due condensati sovrapposti mediante sympathetic cooling e interazione tra i due condensati: atomi di rubidio in due diversi stati sono stati raffreddati simultaneamente fino alla condensazione. Si è dimostrata la possibilità di raffreddare gli atomi in uno stato raffreddando gli atomi nell'altro stato. I risultati ottenuti mostrano che l'interazione tra i due condensati è di tipo repulsivo. c) Confinamento di un condensato in una trappola ottica: dopo aver raggiunto la condensazione in una trappola magnetica, gli atomi sono stati trasferiti in una trappola dipolare. Questo ha permesso di ottenere densità atomiche estremamente elevate. Inoltre, la possibilità di applicare un campo magnetico senza variare le condizioni di confinamento ha permesso di studiare l'effetto del campo sul potenziale di interazione interatomico e di osservare le risonanze di Feshbach, in corrispondenza delle quali l'interazione tra gli atomi varia notevolmente e può trasformarsi da repulsiva ad attrattiva o viceversa. d) Studio di un gas di atomi fermionici: finora le condizioni di degenerazione quantistica sono state raggiunte solo per atomi bosonici, ma sono attualmente in corso esperimenti analoghi su atomi fermionici. Per densità nello spazio delle fasi simili a quelle per le quali si è osservata la condensazione di Bose-Einstein, ci si attendono notevoli differenze nel comportamento collettivo e, per temperature ancora più basse, si dovrebbero poter osservare effetti di superfluidità.

È bene osservare infine che, sebbene gran parte delle informazioni riportate in questa voce si riferiscano agli esperimenti condotti su atomi alcalini, in un esperimento condotto da D. Kleppner e collaboratori nel 1998 sono stati recentemente osservati effetti che indicherebbero la condensazione di atomi di idrogeno. In questo caso per il raffreddamento iniziale non è stato utilizzato il raffreddamento laser ma un criostato, mentre un ruolo fondamentale è ancora svolto dal confinamento magnetico e dal raffreddamento evaporativo. Questo risultato, che corona sforzi durati decenni grazie ai quali molti dei metodi qui descritti sono stati inventati e messi a punto, apre la possibilità di nuovi affascinanti esperimenti.

bibliografia

Laser Manipulation of Atoms and Ions, Atti della scuola internazionale di fisica "Enrico Fermi", Corso cxviii, ed. E. Arimondo, W. Phillips, F. Strumia, Amsterdam 1992.

M. Inguscio, Spettroscopia atomica laser, in Enciclopedia delle Scienze Fisiche, Istituto della Enciclopedia Italiana, 5° vol., Roma 1995.

M. Inguscio, G.M. Tino, Fisica atomica: tecniche recenti di raffreddamento laser, in Enciclopedia delle Scienze Fisiche, Istituto della Enciclopedia Italiana, 6° vol., Roma 1995.

M. Inguscio, G.M. Tino, Experiments on Bose-Einstein condensation, in Rivista del Nuovo Cimento, 1999.

Bose-Einstein condensation in atomic gases, Atti della scuola internazionale di fisica "Enrico Fermi", Corso cxl, ed. M. Inguscio, S. Stringari, C.E. Wieman, Amsterdam 1999.