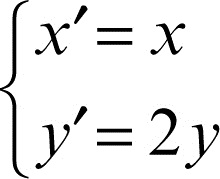figura unita

figura unita

figura unita relativamente a una data trasformazione geometrica ƒ, è detta unita ogni figura F tale che ƒ(F) = F. Per esempio, una circonferenza di centro O risulta unita nella simmetria avente come centro il centro della circonferenza. In tale caso, però, la figura risulta unita come sostegno e non punto per punto, perché la figura corrisponde globalmente a sé stessa, ma a ogni suo punto corrisponde un diverso punto, quello diametralmente opposto.

Se risulta anche ƒ(P) = P per ogni punto della figura F, allora F si dice unita in ƒ punto per punto o anche globalmente fissa. Per esempio, nella trasformazione affine ƒ di equazioni

la retta r di equazione y = 0 risulta fissa, e quindi unita punto per punto, mentre la retta s di equazione x = 2 è unita solo come sostegno, ma non punto per punto, perché subisce una dilatazione.