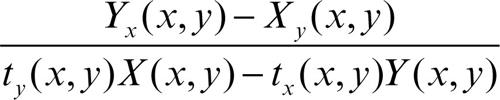fattore integrante
fattore integrante
fattore integrante in analisi, termine utilizzato in una tecnica di soluzione per equazioni differenziali del primo ordine. Se un’equazione viene scritta nella forma X(x, y)dx + Y(x, y)dy = 0, ma non è soddisfatta la condizione Xy = Yx che garantisce l’esattezza locale della forma differenziale, è possibile cercare di moltiplicarla per un termine µ(x, y) in modo che diventi una equazione differenziale esatta (→ equazione differenziale, integrale di una). A tale termine si dà il nome di fattore integrante. Nel caso generale il problema si traduce in un’equazione differenziale alle derivate parziali nell’incognita funzione μ, ma vi sono due casi particolari in cui è agevole trovare un fattore integrante. Il primo è quando il rapporto
dipende solo da x; il secondo quando l’analogo
dipende solo da y. In questi due casi particolari, rispettivamente, le funzioni
sono un fattore integrante per l’equazione differenziale data. Per esempio, l’equazione differenziale
non è esatta, risultando Yx = 0 e Xy = 2y. Tuttavia
quindi un fattore integrante è µ(x) = ex. Infatti, l’equazione ex(x 2 + y 2 + 2x)dx + ex(2y)dy = 0 è esatta, e il suo integrale generale è (x 2 + y 2)ex = C. Più in generale, se si immagina che un fattore integrante possa dipendere dai valori di una opportuna funzione t = t(x, y), si deve verificare se il rapporto
è una funzione q(t), nel qual caso un fattore integrante è