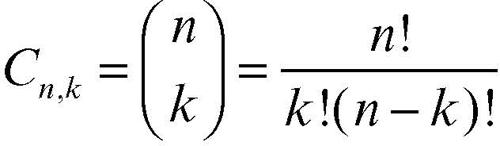estrazioni da un'urna

estrazioni da un'urna

estrazioni da un’urna modelli di simulazione per il calcolo della probabilità in problemi relativi a esperimenti che producano un insieme finito di risultati possibili. Da un’urna, che contiene un definito numero di n oggetti con diverse modalità (tipicamente, palline o gettoni diversamente colorati o numerati, come nel gioco della tombola o del lotto; biglietti con numeri o nomi come in una lotteria) si estraggono con modalità diverse uno o più oggetti. Se ogni volta si estrae un oggetto, si distinguono due casi:

• estrazione con reimbussolamento (o con reimmissione) in cui, per l’estrazione successiva, l’oggetto estratto viene reintrodotto nell’urna. In questo caso il numero totale di oggetti nell’urna e la sua composizione si mantengono costanti nelle successive estrazioni e quindi il numero dei casi possibili, alla base del calcolo della probabilità dell’estrazione dell’oggetto, resta invariato. Tale modello genera una successione di eventi indipendenti, per i quali cioè, qualunque sia l’evento in esame, la probabilità in ogni estrazione rimane invariata e lo stesso oggetto può essere estratto più volte;

• estrazione senza reimbussolamento (o senza reimmissione), in cui l’oggetto estratto non viene reinserito nell’urna. In tale caso, si genera una successione di eventi dipendenti, in cui vanno ricalcolate le probabilità sulla base di ciò che è stato estratto, giacché ogni volta si modifica la composizione dell’urna stessa.

Il caso di estrazioni in blocco di k oggetti su un totale di n (con 2 ≤ k ≤ n), cioè con estrazione simultanea di k elementi dell’urna, va trattato come quello di una successione di k estrazioni senza reimbussolamento. Il numero delle possibili diverse estrazioni in blocco di k elementi su n è dato dal numero delle combinazioni di classe k:

Al modello delle estrazioni da un’urna fa riferimento anche la statistica quando estrae con una procedura casuale una o più unità statistiche da una popolazione per studiarne uno o più caratteri.