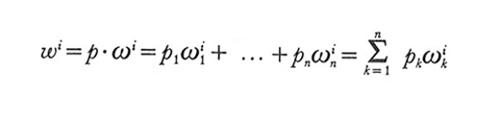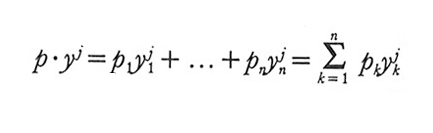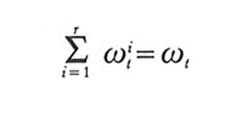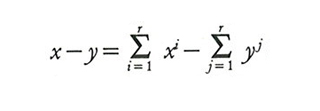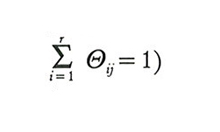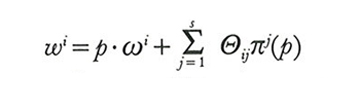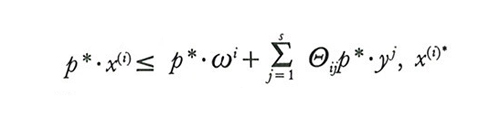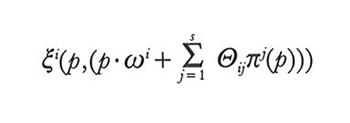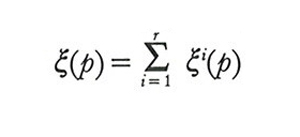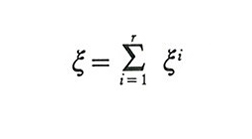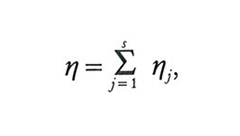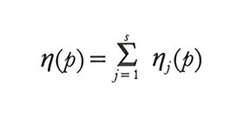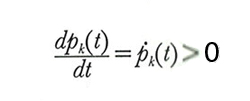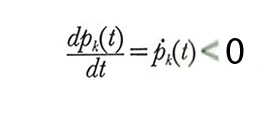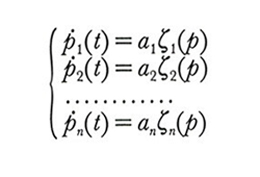Equilibrio economico

Equilibrio economico

Il concetto di equilibrio economico

Fin dalla seconda metà del Settecento gli studiosi che si sono occupati di economia hanno fatto uso del concetto di equilibrio economico per analizzare i fenomeni della produzione, del consumo e dello scambio. Nel corso dell'Ottocento questo concetto ha man mano acquisito un ruolo centrale nei tentativi di trasformare la giovane scienza economica in una scienza quantitativa avente le stesse caratteristiche di rigore e oggettività e metodi analoghi a quelli della fisica-matematica. La teoria dell'equilibrio economico generale, la cui prima formulazione compiuta è dovuta all'economista francese Léon Walras (1834-1910), è considerata da molti interpreti come il fondamento della teoria economica contemporanea in cui il concetto di equilibrio riveste un ruolo fondamentale.

L'indirizzo di pensiero ispirato dalla teoria dell'equilibrio economico generale si differenzia da altre correnti teoriche contemporanee (come la teoria che riprende la tradizione classica inglese, la teoria evolutiva di Alfred Marshall, la teoria della disoccupazione involontaria di John Maynard Keynes e della scuola keynesiana, la teoria di Schumpeter), ma non perché sia l'unico a utilizzare il concetto di equilibrio. Questo concetto, infatti, è stato usato ed è tuttora correntemente usato anche in accezioni diverse e secondo definizioni diverse da quella adottata nella teoria walrasiana. Nei capitoli che seguono accenneremo ai diversi concetti di equilibrio ma ci soffermeremo sulle idee e sui problemi della teoria dell'equilibrio economico generale.

Quello di equilibrio economico è un concetto che descrive uno stato possibile del sistema economico, definito idealmente da particolari proprietà. Questo stato ideale del sistema economico è l'oggetto di una riflessione teorica tesa a definire modelli capaci di rappresentarlo con chiarezza e precisione e a ottenere risultati interessanti circa le sue proprietà.

I problemi che nascono in questa riflessione possono così riassumersi: come è descritto il sistema economico di cui si vuol studiare questo stato ideale? come sono definite le proprietà che caratterizzano tale stato ideale? su quale arco di tempo si osserva il sistema economico quando se ne considera uno stato di equilibrio? perché - infine - viene attribuita tanta importanza allo stato di equilibrio?

Iniziamo col descrivere brevemente il contesto teorico entro cui vengono esaminati questi problemi e precisamente la nozione di sistema economico. Il sistema economico è caratterizzato, in questa teoria, da tre elementi: le merci, i prezzi e l'attività degli agenti economici. Una merce è da intendere come un bene (presente in natura o risultato dell'attività produttiva) o una prestazione di attività lavorativa o di servizi ed è caratterizzata da tre elementi: la sua quantità fisica, la sua collocazione nello spazio, la sua collocazione nel tempo. Il prezzo è un numero che definisce ciò che deve essere pagato ora, in termini della quantità di una data merce, per ottenerne un'altra: esso definisce quindi i rapporti di scambio ed è anche un indicatore della 'scarsità' delle merci. Gli agenti economici sono i produttori e i consumatori. I primi sono mossi nella loro attività (la produzione di merci) dall'intento di rendere massimo il proprio profitto. I secondi si scambiano le merci nell'intento di 'massimizzarne l'utilità', ovvero di soddisfare, al livello massimo consentito, un sistema di 'preferenze' che guida le loro scelte. Gli uni e gli altri sono mossi dalla spinta a ottenere il massimo vantaggio possibile (insaziabilità). Si suppone che essi agiscano sulla base di un piano perfettamente determinato (il che presuppone una capacità di previsione perfetta): questa ipotesi ha come conseguenza il carattere strettamente deterministico del sistema economico.

Tre proprietà sono state usate, in numerose varianti, per definire lo stato di equilibrio del mercato. In base alla sua prima e più intuitiva caratterizzazione lo stato di equilibrio è uno stato dell'economia che, una volta raggiunto, permane, o, più precisamente, è uno stato che il sistema economico tende spontaneamente a raggiungere e a conservare invariato. Questa nozione intuitiva, secondo cui l'equilibrio economico è uno stato di invarianza del mercato e allo stesso tempo è un punto di arrivo cui tende l'evoluzione del mercato, è stata oggetto di sofisticate elaborazioni formali che ne hanno di volta in volta reso preciso il significato mediante diversi modelli matematici.

In secondo luogo, l'equilibrio economico è concepito come uno stato in cui ciascun agente economico si trova in una posizione ottimale, tenuto conto delle limitazioni ('vincoli') che gli sono imposte dalle scelte degli altri agenti e dalle risorse di cui egli stesso dispone o che sono globalmente disponibili nell'economia. Nello stato di equilibrio ogni scambista sceglie i comportamenti e i piani che più gli convengono secondo criteri di ottimalità.

Infine lo stato di equilibrio è inteso come uno stato di coerenza dei piani e di compatibilità delle scelte dei singoli operatori, scelte che possono pertanto essere tradotte in un sistema di scambi coerente e realizzabile, nel senso che nessuno si troverà nell'impossibilità di scambiare ciò che ha programmato in quanto non compatibile con le decisioni degli altri agenti. Questa proprietà dello stato di equilibrio è variamente rappresentata da condizioni di uguaglianza tra domanda e offerta sui mercati.

È spontaneo chiedersi perché il concetto di equilibrio abbia avuto un ruolo tanto centrale nella teoria economica. La risposta è che dietro la scelta di questo concetto vi è una 'visione', per usare un termine caro a Schumpeter, una concezione del mondo dei fenomeni economici che ha indirizzato la scelta dei modelli e dei termini utilizzati. La concezione è quella secondo cui il comportamento degli agenti economici porta in modo naturale l'economia verso una condizione di compatibilità dei differenti fini. Data questa concezione, che costituisce una premessa 'metafisica' e indimostrabile della teoria, obiettivi dello studio diventano la caratterizzazione dell'evoluzione spontanea postulata e la scoperta delle condizioni sotto le quali si manifesta lo stato di compatibilità.

In questa 'visione' la compatibilità dei fini nello stato di equilibrio del mercato è caratterizzata dalla proprietà dell'ottimalità: gli operatori si trovano nello stato di equilibrio 'meglio' che in altri stati, in quanto in esso realizzano le loro scelte preferite. Intervengono così nozioni come quella di maggior benessere e di migliori condizioni del sistema, la cui introduzione ha dato luogo a lunghi dibattiti per pervenire alla definizione rigorosa di cosa debba intendersi per ottimalità a livello delle scelte di una collettività e non di un singolo. I problemi che si ponevano possono essere riassunti nelle seguenti domande: è possibile misurare il benessere di una collettività? si può in alternativa adottare un criterio di confronto tra stati del sistema economico per decidere quale sia ottimale ed entro quali limiti?

Una definizione esatta della nozione di ottimalità fu data da Vilfredo Pareto (1848-1923). Secondo tale definizione, uno stato ottimale (o 'efficiente nel senso di Pareto') è uno stato in cui non è possibile migliorare la soddisfazione di un agente senza diminuire quella di almeno un altro agente. Questa nozione precisa ha inaugurato un filone di ricerca tendente a mostrare l'esistenza di ottimi nel senso di Pareto e a studiare la relazione di questa nozione con quella di equilibrio. Si è così mostrato non soltanto che un ottimo di Pareto esiste, sotto condizioni piuttosto generali, ma anche che un equilibrio economico relativo a un dato sistema di prezzi è un ottimo di Pareto e viceversa (v. Debreu, 1959; v. Arrow e Hahn, 1971).

Diamo ora una sommaria idea delle diverse nozioni di equilibrio che sono state introdotte nella teoria economica.

Un ruolo importante (e anticipatore) ha avuto l'analisi dell'equilibrio parziale: l'equilibrio tra la domanda e l'offerta nel mercato di un solo bene considerato isolatamente. I primi modelli matematici di equilibrio parziale furono costruiti da Antoine-Augustin Cournot (1801-1877), matematico e filosofo francese, nel testo Recherches sur les principes mathématiques de la théorie des richesses pubblicato nel 1838. In questo testo Cournot distingueva le situazioni di mercato in base al numero delle imprese presenti dal lato dell'offerta e individuava tre principali forme di mercato: il monopolio (un unico produttore), il duopolio (due produttori), la concorrenza indefinita (molti produttori ciascuno di dimensioni modeste rispetto al mercato, così da non essere in grado di influire individualmente con la propria produzione sulle condizioni generali dell'offerta). L'analisi parziale di Cournot permetteva di studiare le proprietà dell'equilibrio nelle diverse forme di mercato.

Nell'analisi di equilibrio parziale si considerano la domanda dei consumatori e l'offerta dei produttori come funzioni del prezzo della merce scambiata nel mercato sul quale si vuole concentrare l'attenzione. L'equilibrio è lo stato del mercato caratterizzato da un prezzo della merce (il prezzo di equilibrio), al quale la domanda espressa dai consumatori e l'offerta espressa dai produttori sono eguali. Tutti i modelli di equilibrio parziale si fondano, quindi, sull'ipotesi che sia possibile, per semplicità, isolare ciò che accade su un mercato da ciò che accade sugli altri mercati del sistema economico, senza che l'indagine perda rilevanza teorica. I modelli di equilibrio economico generale vogliono invece sottolineare le relazioni tra gli scambi che avvengono sui diversi mercati di un'economia. L'equilibrio generale è lo stato dei mercati (anch'esso definito da un sistema di prezzi di equilibrio) in cui, su tutti i mercati presenti nel sistema economico, la domanda globale del mercato e l'offerta globale del mercato - ovvero le somme rispettive di tutte le domande e di tutte le offerte individuali su ciascun mercato - sono eguali. I modelli di equilibrio generale, come vedremo, vanno incontro a grandi difficoltà formali, per la complessità delle interrelazioni tra i mercati che intendono porre in evidenza. I modelli di equilibrio parziale, benché più elementari, sono stati preferiti da molti economisti, proprio perché ritenuti più maneggevoli e tuttavia efficaci per descrivere situazioni di mercato circoscritte, per analizzare i problemi particolari di un settore industriale, per definire le forme di mercato (monopolio, oligopolio, concorrenza perfetta), per studiare gli scambi di determinati tipi di beni.

Il metodo dell'equilibrio parziale fu adottato in particolare dall'economista inglese Alfred Marshall (1842-1924) nel suo trattato Principles of economics, pubblicato nel 1890. Marshall studiava l'equilibrio di ciascun mercato isolatamente come equilibrio dell'industria, ponendo l'accento sull'evoluzione e l'adattamento della struttura produttiva (imprese, impianti, manodopera, reti di vendita) alle condizioni della domanda finale espressa dai consumatori.

A seconda dell'arco di tempo entro il quale questo adattamento poteva aver luogo, Marshall distingueva tre diversi equilibri del mercato: l'equilibrio del giorno di mercato, l'equilibrio di breve periodo, l'equilibrio di luogo periodo. L'equilibrio del giorno di mercato è l'equilibrio tra domanda e offerta, che si realizza spontaneamente in un mercato in condizioni di concorrenza, quando gli scambi si svolgano in un arco di tempo molto breve: la struttura produttiva dell'industria è data, le imprese hanno già deciso i livelli di produzione e portato al mercato la propria offerta, il prezzo di mercato si fissa al livello in corrispondenza del quale l'intera offerta sul mercato viene assorbita dalla domanda dei consumatori. Nell'equilibrio di breve periodo, che si determina in un arco di tempo più lungo, i livelli di produzione possono essere adattati dalle imprese per sfruttare le opportunità di profitto offerte dalle condizioni della domanda. In un arco di tempo ancora più lungo anche la struttura produttiva dell'intera industria si potrà modificare fino a raggiungere le condizioni di efficienza e minimizzazione dei costi (equilibrio di lungo periodo) che, secondo la teoria di Marshall, caratterizzano le imprese in condizioni di concorrenza.

L'idea che si possa isolare idealmente uno stato del sistema economico in cui la struttura produttiva sia data e le imprese adattino la propria offerta alle condizioni della domanda sulla base delle aspettative di profitto fu ripresa da J.M. Keynes nella General theory of employment, interest and money, pubblicata nel 1936, una riflessione teorica sulle gravi difficoltà delle economie di mercato nella crisi degli anni trenta. Keynes introdusse la nozione di equilibrio di sottoccupazione: l'equilibrio che si determina in un'economia nel breve periodo quando l'attività produttiva delle imprese ristagna a livelli di sottoutilizzo degli impianti e una parte delle forze di lavoro non trova occupazione, pur essendo disponibile a lavorare accettando le retribuzioni correnti di mercato. Questa nozione estendeva all'intero sistema economico l'idea marshalliana dell'equilibrio di breve periodo, con la particolarità di considerare come equilibrio, ovvero come stato nel quale il sistema economico tende a persistere, una situazione dei mercati caratterizzata dalla disoccupazione delle risorse e cioè, in primo luogo, dallo squilibrio tra la domanda e l'offerta sul mercato del lavoro.

Per questa singolare combinazione di analisi di equilibrio ed enfasi sull'eccesso di offerta nel mercato del lavoro, la definizione di Keynes è stata molto criticata nel dibattito successivo alla pubblicazione della General theory of employment, interest and money e ancora nel dibattito recente. Ciò nonostante, la nozione di equilibrio macroeconomico di breve periodo con disoccupazione delle risorse (in particolare della risorsa lavoro) è entrata a far parte della teoria economica contemporanea ed è correntemente usata nella letteratura.Molte controversie ha suscitato anche l'idea di equilibrio di lungo periodo, per la difficoltà di combinare in modo coerente lo studio del cambiamento dell'apparato produttivo nel tempo e l'ipotesi dell'invarianza dei dati e del contesto, che caratterizza i modelli di equilibrio parziale.

Il fatto di considerare il tempo esplicitamente (e quindi non soltanto come una variabile formale) complica enormemente il concetto di equilibrio anche nei modelli di equilibrio generale, perché introduce elementi di variabilità nel comportamento di mercato degli operatori e implica la considerazione di un contesto concettuale non deterministico. Ciò comporta sottili problemi logici nella definizione dell'ottimalità e della compatibilità delle scelte. La coerenza dei piani individuali e la compatibilità delle scelte degli operatori possono riguardare soltanto le scelte presenti oppure le scelte che interessano un arco di tempo più lungo o persino le scelte che interessano tutto il futuro, nei modelli più astratti. Le scelte economiche che si proiettano nel futuro comportano delle aspettative, sia perché impegnano oggi risorse e redditi che saranno disponibili nel futuro, sia perché promettono consegne di beni non ancora effettuate e quindi sono espressione di piani di produzione e scambio non ristretti al presente: sono scelte dettate dall'aspettativa che nel futuro prevarranno certe condizioni attese, che un evento o un insieme di eventi avranno o non avranno luogo. Se esplicitiamo il dato che gli agenti economici fanno scelte e svolgono la loro attività nel corso di successivi periodi di tempo, allora dobbiamo anche tener conto esplicitamente del fatto che anche i piani di scambio formulati nel periodo presente per essere immediatamente realizzati sono parte di scelte e progetti che si fondano su aspettative circa eventi futuri, scelte e progetti che gli agenti potranno rivedere e correggere alla luce delle conferme che riceveranno dai fatti o degli errori di previsione. La scelta di piani ottimali è una scelta intertemporale, che investe una successione di periodi e comporta un complicato processo di formazione e verifica delle aspettative.

Queste considerazioni fanno intendere che sono possibili diverse nozioni di equilibrio, per descrivere l'intricata rete di relazioni che si stabiliscono sui mercati quando si vogliano rappresentare l'ottimalità e la compatibilità di piani intertemporali, che hanno attuazione nel corso del tempo. Le difficoltà logiche e formali che emergono nella trattazione del tempo, nell'ambito della teoria dell'equilibrio economico generale, sono state oggetto di dibattito e riflessione soprattutto durante gli anni venti e trenta del XX secolo. In quel periodo tre studiosi, l'austriaco Friedrich A. von Hayek, lo svedese Erik Lindahl, l'inglese John Hicks, hanno contribuito a definire il concetto di equilibrio temporaneo, rappresentando gli scambi sui mercati come una successione di stati di equilibrio condizionati dalle aspettative circa il futuro degli agenti economici e dalle risorse e dall'apparato produttivo che l'economia ha ereditato dai periodi precedenti. Nei modelli di equilibrio temporaneo gli scambi sono o contrattati e attuati in ciascun periodo (scambi a pronti, cioè a consegna immediata) o contrattati per essere attuati più tardi (scambi a termine, cioè a consegna differita). La compatibilità delle scelte, ovvero lo stato di equilibrio, che si realizza in ognuno di questi periodi non è però garanzia di compatibilità e ottimalità dei piani per tutta la successione dei periodi, vale a dire anche relativamente ai periodi futuri, quando gli agenti potranno rivedere le proprie scelte, correggere le proprie aspettative, contrattare e attuare nuovi scambi. Una successione di stati dell'economia, nella quale gli agenti economici non debbano mai rivedere le proprie aspettative sugli eventi futuri, perché l'andamento del mercato conferma le loro previsioni, prende il nome di equilibrio con aspettative confermate.Per aggirare le difficoltà poste dal fatto di considerare il tempo, si è preferito adottare un modello artificioso, che rappresenta il caso particolare di un sistema economico nel quale tutti gli scambi sono contrattati in un unico momento iniziale, per essere poi attuati, secondo i contratti stabiliti, nel corso dei successivi periodi di tempo. Lo stato di equilibrio che si determina in questa particolarissima economia di mercati a termine completi, nella quale sono progettati e contrattati nel periodo iniziale tutti gli atti di scambio e di produzione che saranno realizzati in futuro, prende il nome di equilibrio intertemporale, perché rappresenta appunto uno stato di coerenza e compatibilità delle scelte ottimali degli agenti economici che si estende a tutto il futuro. A questo modello dedicheremo il seguito della nostra trattazione.

La teoria dell'equilibrio economico generale nel suo profilo storico

L'ambizione della teoria dell'equilibrio economico generale, dalle origini fino ai suoi sviluppi recentissimi, e quindi l'aspirazione degli autori che l'hanno sviluppata, è stata quella di produrre una teoria scientifica rigorosa, formulata mediante una struttura matematica internamente coerente, che permettesse di ottenere delle dimostrazioni dei risultati previsti. Benché la teoria sia stata formulata agli inizi in un linguaggio matematico molto elementare, se non primitivo, i problemi che affrontava erano i medesimi che costituiscono ancora l'oggetto delle ricerche enormemente più sofisticate di oggi.

L'idea fondamentale della teoria è quella dell'interdipendenza dei mercati: i prezzi relativi sono determinati dall'interazione tra domanda e offerta su tutti i mercati. Poiché uno stato di equilibrio è definito da un sistema di prezzi di equilibrio, l'oggetto principale della teoria è sempre stato la determinazione dei prezzi in un mercato di concorrenza perfetta. L'assunto metodologico fondamentale è che ciò che avviene sul mercato nell'aggregato è determinato dalla somma delle scelte dei singoli produttori e consumatori e che queste scelte possono essere rappresentate in modo chiaro e completo a partire dalle preferenze degli individui e dalle tecnologie produttive delle imprese. I prezzi di equilibrio sono determinati dall'interazione tra le scelte razionali dei singoli e i vincoli posti dalla tecnologia e dalla disponibilità delle risorse. L'ipotesi della concorrenza perfetta esprime l'idea che i singoli agenti, consumatori o imprese, non siano in grado di influire con interventi consapevoli sul risultato di questa interazione e nelle loro decisioni debbano assumere come un dato i prezzi relativi espressi dal mercato. Questa ipotesi si enuncia dicendo che gli agenti sono price-takers.

Proprio in quanto così determinati, i prezzi sono gli unici segnali che permettono di condurre il sistema dei mercati interdipendenti (di concorrenza perfetta) all'equilibrio. Un dato sistema di prezzi relativi determina l'eccesso di domanda dei vari mercati; se tale eccesso non è nullo, il sistema dei prezzi si modificherà in modo che la domanda e l'offerta si avvicinino a uno stato di eguaglianza. La modificazione seguirà la legge della domanda e dell'offerta: il prezzo in un mercato cresce in corrispondenza di un eccesso positivo della domanda e decresce in corrispondenza di un eccesso di domanda negativo. Tale processo di aggiustamento dei prezzi (chiamato da Walras tâtonnement) non deve essere concepito come un processo consapevolmente guidato (come accadrà nella reinterpretazione moderna del concetto di equilibrio nell'ambito delle teorie della pianificazione), bensì come un meccanismo di autoregolazione dei mercati, che, guidati da una sorta di 'mano invisibile' (secondo l'espressione di Adam Smith), vengono spontaneamente condotti all'equilibrio. Un mercato di concorrenza perfetta tende all'equilibrio tra domanda e offerta e lo raggiunge attraverso aggiustamenti dei prezzi relativi, che cessano solo quando si raggiunge appunto un sistema di prezzi di equilibrio.

Nonostante le formulazioni precedenti si ispirino alle versioni più moderne della teoria dell'equilibrio economico, non c'è dubbio che i concetti sottostanti operano anche nelle prime versioni di tale teoria. I problemi storiografici che si pongono sono allora quelli di analizzare come si sia formato il concetto di equilibrio economico, come si sia perfezionato e affinato e, allo stesso tempo, come gli economisti che hanno sviluppato questo filone di pensiero abbiano elaborato i criteri di scientificità che intervengono nella costruzione della teoria.

Questi problemi storiografici si intrecciano strettamente ai problemi di carattere analitico: la dimostrazione della coerenza interna della teoria, la verifica empirica dei suoi risultati, l'applicabilità dell'apparato teorico ai fenomeni reali.

Nell'evoluzione della teoria dell'equilibrio economico generale possiamo distinguere quattro grandi tappe: 1) una prima fase di gestazione del concetto di equilibrio economico, che prende forma nella cultura francese del tardo illuminismo e si ispira direttamente al concetto di equilibrio della meccanica; 2) una seconda fase di formazione e consolidamento della teoria, nell'opera di Walras e Pareto, in cui si definiscono il nucleo paradigmatico della teoria e i suoi concetti fondamentali sotto l'evidente influsso dei concetti e dei metodi della fisica matematica classica; 3) una terza fase in cui la teoria, dopo la crisi della versione precedente, rinasce negli anni trenta del nostro secolo nell'ambiente scientifico di lingua tedesca (a Vienna, in particolare) e vengono poste le basi di una linea di sviluppo assiomatica; 4) la fioritura negli Stati Uniti, a partire dagli anni quaranta, dei programmi di assiomatizzazione della teoria e quindi degli sviluppi che la teoria ha conosciuto fino a oggi, attraverso varie peripezie metodologiche e concettuali.

La prima formulazione del concetto di equilibrio economico è un prodotto del pensiero filosofico e scientifico del XVIII secolo nell'ambito della nascente scienza della società. Questo concetto e le sue prime definizioni scientifiche sono ispirati da un tema centrale della cultura illuminista (e soprattutto tardoilluminista): la centralità e il valore universale della scienza fisico-matematica newtoniana, le enormi speranze suscitate dalle sue conquiste in ogni campo del sapere, l'impulso che tale scienza trasmette a costruire nuove regulae philosophandi nella storia, nel diritto, nella teoria politica. Uno dei risultati più evidenti di tale clima culturale è l'emergere nelle scienze sociali della nozione di 'legge', intesa come 'legge naturale'. Il modello da imitare, per determinare le leggi scientifiche della società, è la meccanica newtoniana, di cui uno dei concetti centrali è quello di equilibrio meccanico (statico o dinamico che sia). È possibile seguire con precisione (v. Ingrao e Israel, 1987) l'emergere progressivo di questo concetto nell'opera dei fisiocratici e in particolare nel pensiero di Anne-Robert-Jacques Turgot (1727-1781) e di Pierre-Samuel Dupont de Nemours (1739-1817).

Non va trascurato, inoltre, il clima generale di sviluppo delle applicazioni della matematica a tematiche di carattere sociale e biologico, che è bene espresso dalle ricerche nel campo della arithmétique politique e che spingerà il marchese di Condorcet (1743-1794) alla formulazione di un ambizioso programma di mathématique sociale, di cui l'economia politica costituisce soltanto un aspetto. Tali ricerche saranno proseguite nel contesto delle attività della Classe de Sciences Morales et Politiques dell'Institut de France (v. Israel, 1991), che è il centro di attività del gruppo degli idéologues. Sarà proprio la Classe a premiare, nel 1801, quello che può essere considerato il primo testo contenente una formulazione esplicita del concetto di equilibrio economico e un primo tentativo coerente di matematizzazione della teoria dello scambio e della determinazione dei prezzi. Si tratta di un libro del matematico francese Nicolas-François Canard (1750-1833). In questo testo (v. Canard, 1801) l'equilibrio parziale è paragonato all'equilibrio statico di una leva, mentre l'equilibrio generale del mercato è rappresentato attraverso una metafora tratta dalla meccanica dei fluidi: il sistema economico è assimilato a un sistema di canali intercomunicanti in cui le acque raggiungono uno stato di equilibrio. Si noti che l'analogia idrodinamica è ispirata a sua volta dal parallelismo fra il processo di circolazione del sangue e l'equilibrio economico (inteso in forma dinamica), che è un tema classico del pensiero fisiocratico. Da questa fonte Canard lo ha ripreso. Il tentativo di Canard è per molti versi assai ingenuo, ma contiene in nuce parecchi concetti importanti che saranno ripresi nell'opera di Cournot e Walras. Fra di essi troviamo, in forma embrionale, un'idea del processo di aggiustamento dei prezzi (tâtonnement). Il lavoro di Canard e la parallela fioritura di lavori di matematica sociale, che spaziano dalla demografia alla teoria giuridica e politica, ai problemi di debito pubblico, alla statistica sanitaria, cadono infine nel discredito per un processo complesso di mutamento che si verifica nella cultura francese e che ha anche risvolti direttamente politici: il dispotismo napoleonico, l'esaurirsi del razionalismo utopistico riformatore dell'epoca rivoluzionaria, la separazione disciplinare che tende ad allontanare le scienze esatte dalle altre scienze. Anche nel gruppo degli idéologues prevale la tendenza a perseguire un progetto di costruzione della scienza sociale che rifiuta radicalmente la matematizzazione. L'economista Jean-Baptiste Say (1767-1832) è una figura di spicco di questa tendenza.

Si determina così una svolta che renderà l'ambiente della scienza sociale francese ostile alla matematizzazione, un'ostilità che sarà poi amaramente sperimentata da Cournot e da Walras. Questa ostilità si sviluppa anche negli ambienti delle scienze fisico-matematiche, che pure erano stati così sensibili alle tematiche dell'arithmétique politique e della mathématique sociale e avevano visto manifestarsi l'interesse diretto per queste discipline da parte di scienziati di primo piano come Bernoulli, Condorcet, Lagrange, Vandermonde e Laplace. In estrema sintesi ciò è conseguenza del prevalere di una visione romantica, che nega la possibilità di esprimere 'in numeri', e cioè di studiare quantitativamente, questioni che toccano la libertà del soggetto sociale, la quale appare (in pieno conflitto con la visione prevalente nel materialismo settecentesco) come irriducibile a uno studio scientifico esatto. Da un lato ciò si esprime, nel mondo delle scienze fisico-matematiche, nel prevalere di una 'ripugnanza' per l'applicazione del calcolo alle cose dell'ordine morale, per l''aberrazione' consistente nell'"assimilare l'uomo a un dado" (per usare le parole del fisico-matematico Louis Poinsot, allievo di Laplace). E dall'altro lato, nel mondo delle scienze sociali, nel prevalere del metodo storico. Questa sostanziale convergenza stronca lo sviluppo scientifico di quelle discipline che trovano uno spazio di sviluppo in ambienti marginali rispetto alla scienza 'ufficiale', come quelli degli ingegneri o dei cultori della statistica. (Di particolare interesse, in questo contesto, è il contributo di Jules Dupuit, 1804-1866). Poiché la polemica si appunta soprattutto sull'uso del calcolo delle probabilità, cui viene negato uno status epistemologico di pari dignità con il punto di vista del determinismo e del calcolo infinitesimale, un margine sottilissimo viene lasciato all'uso di un punto di vista direttamente plasmato su quello della meccanica.

È proprio in questa stretta fessura che si fa strada l'opera fondamentale di Cournot. Cournot è ormai del tutto lontano dai grandi progetti riformatori, finalizzati alla felicità del genere umano, tipici del pensiero illuministico ed è anche molto più prudente di quanto sarà poi Walras nel valutare la portata del progetto di matematizzazione dell'economia: egli si limita alla formulazione di teorie parziali, con molti distinguo sulla loro applicabilità. In coerenza con questo atteggiamento egli prende energicamente le distanze dal tentativo pioneristico di Canard, pur ispirandosi con ogni evidenza a diverse idee dell'ingenuo professore francese di matematica e mostrando a più riprese di trarre spunto dall'analogia meccanica. L'originalità del progetto di Cournot (v., 1838) consiste nell'aver indicato la via dell'uso della teoria delle funzioni nello studio dei problemi economici, senza la necessità di specificare la forma delle funzioni che descrivono le leggi studiate, se non in termini di proprietà analitiche molto generali. Non c'è dubbio che questo indirizzo astratto e assolutamente alieno da ogni applicazione numerica diretta ha plasmato gli sviluppi di tutta la teoria dell'equilibrio economico generale fino ai nostri giorni. Oltre a questo contributo metodologico fondamentale, i contributi specifici più importanti di Cournot sono la chiara enunciazione della legge che regola in un singolo mercato la relazione fra la quantità domandata del bene scambiato e il prezzo in moneta del bene stesso (loi du débit) e, come abbiamo già ricordato, la definizione delle 'forme' fondamentali del mercato, che nella teoria del duopolio anticipa e imposta l'analisi contemporanea dei mercati di oligopolio.

Tuttavia, per le ragioni sopra illustrate, il mondo scientifico e il mondo degli economisti erano ormai poco disposti a interessarsi a un siffatto approccio e l'opera di Cournot cadde in un silenzio quasi totale, al punto che nella sua opera successiva (v. Cournot, 1863), che riproponeva i contenuti della precedente, Cournot espunse tutte le formule matematiche. Con questo silenzio si chiuse la prima fase di gestazione del concetto di equilibrio, ma ormai erano stati gettati i semi di un progetto scientifico che continuò a sopravvivere in forma sotterranea.

Tale progetto si basava su un'idea che riemerse in Walras come in Pareto (e in molti altri autori, tra i quali ricordiamo William Stanley Jevons, Irving Fisher e Paul Samuelson): l'idea che i concetti della meccanica possano, una volta spogliati del riferimento specifico ai fenomeni fisici, costituire un repertorio di concetti astratti utilizzabili per una rappresentazione efficace dei fenomeni di mercato, e che a questo repertorio si debba attingere a piene mani, perché esso offre una sorta di materia prima concettuale già elaborata e sperimentata in una scienza solida come la fisica. Quest'idea è la premessa per il pieno sviluppo del concetto di equilibrio nell'opera di Walras, più precisamente nel testo che raccoglie le sue lezioni universitarie, pubblicato col titolo Éléments d'économie politique pure ou théorie de la richesse sociale (v. Walras, 1874-1877).

Nell'opera di Walras il progetto di creare un'economia politica pura in forma matematica, secondo il modello scientifico della meccanica classica e dell'astronomia newtoniana, diviene un progetto articolato e compiuto. Walras mutuò lo scheletro delle equazioni dell'equilibrio dal trattato di statica di Poinsot e attinse dalla meccanica classica non solo, e non tanto, gli strumenti matematici, ma anche, e soprattutto, un sistema di concetti per descrivere e interpretare i fenomeni di mercato. Ciò emerge con chiarezza nella discussione metodologica che Walras premise alla sua costruzione teorica: la distinzione tra tipi reali e tipi ideali di mercato e la descrizione di come si passi dalla definizione dei primi all'analisi formale per teoremi e dimostrazioni. Il mercato di concorrenza perfetta è concepito da Walras come la rappresentazione ideale, senza 'attriti', del tipo reale del 'mercato d'asta', che è scelto a sua volta come la forma tipica del mercato tout court. Il tâtonnement è la rappresentazione astratta e depurata di aspetti accessori ('attriti') del meccanismo di funzionamento di un mercato d'asta, costruita per mostrare, attraverso i concetti puri della teoria, come i mercati di concorrenza convergano verso lo stato di equilibrio. Per Walras il tâtonnement è una sorta di simulazione ideale di ciò che accade effettivamente nei mercati, una rappresentazione ideale di come si svolgerebbero i fenomeni dello scambio in mercati che si avvicinassero alle condizioni ideali della concorrenza perfetta.

L'ultimo scritto di Walras (v., 1909) è un breve saggio tutto dedicato a convincere i "contraddittori matematici" che vi è perfetta analogia tra la teoria dell'equilibrio economico walrasiana e due temi centrali della meccanica: l'equilibrio della bilancia e le equazioni della gravitazione universale. Walras arriva a concludere che l'economia è una scienza 'psichico-matematica' del tutto analoga alle scienze fisico-matematiche, salvo il fatto che si occupa appunto di grandezze psichiche anziché fisiche. Nella corrispondenza di Walras (v. Jaffé, 1965) un intero carteggio è dedicato alla discussione puntuale e precisa di questa analogia, che egli considera fondamentale al fine di convincere i fisici e i matematici della solidità scientifica della nuova disciplina. Con insistenza accanita Walras si rivolse, infatti, ai fisici e ai matematici dell'epoca per ricevere approvazione e incoraggiamento al suo programma scientifico.

Nel programma di Walras era presente un problema aperto e irrisolto: la relazione tra l'anima normativa e l'anima descrittiva della teoria dell'equilibrio economico. Fin dal XVIII secolo il progetto di trasferire il concetto di legge dalle scienze fisiche alle scienze sociali aveva sollevato il problema della compresenza, nelle scienze sociali, di due facce del concetto di legge: da un lato la regolarità dei fenomeni e la loro causalità indipendente dal volere dell'uomo, dall'altro la norma della ragione e quindi il precetto dell'azione sociale. Questo conflitto - o duplicità di significato - insito nel concetto di 'legge naturale' esteso al mondo dei fenomeni umani è presente in Montesquieu, in Condorcet, nella fisiocrazia. Lo ritroviamo nell'opera di Walras, che discende, per aspetti importanti, dalla teoria del diritto naturale. Per i teorici del diritto naturale la legge naturale ha il carattere di una verità certa ed evidente di tipo deduttivo, come le verità della geometria, e non è indotta a partire da regolarità osservate nel mondo umano, né smentita dalle assurdità della storia. Per Walras l'equilibrio di concorrenza perfetta, prima ancora di essere il modello astratto di un'organizzazione sociale esistente, è una norma della ragione, un ideale di organizzazione sociale cui tendere. L'equilibrio economico generale è un ideale normativo più che una fotografia della realtà dei mercati. Come si concili questa concezione normativa dell'equilibrio con la concezione meccanicistica mutuata dalla fisica classica è il problema interpretativo più delicato che si presenti allo studioso dell'opera di Walras.

Nell'opera di Vilfredo Pareto (1848-1923) la difficile convivenza divenne un'aperta contraddizione, che portò in definitiva Pareto a spostarsi sul terreno della sociologia. Pareto, un ingegnere italiano, era anche più radicato di Walras nella cultura scientifica del suo tempo. Contrariamente a Walras, aveva avuto una formazione scientifica regolare presso il Politecnico di Torino, che era allora un centro molto vivo di dibattito scientifico e un'ottima scuola di meccanica. Il suo programma scientifico fu subito informato, a differenza di quello di Walras, a una esigenza preminente di fondazione empirica della teoria, perché Pareto considerava il metodo sperimentale cardine e fondamento di ogni discorso scientifico. Nella costruzione della teoria dell'equilibrio Pareto fu guidato ancor più di Walras dall'idea dell'analogia meccanica. Nel suo Cours (v. Pareto, 1896-1897) egli inserì una tabella a doppia entrata delle corrispondenze tra fisica e teoria economica, ribadendo sia in quest'opera che nel Manuale (v. Pareto, 1906) che l'equilibrio di un sistema di punti materiali della meccanica offre alla teoria economica un sistema di concetti già ben costruito per ragionare sull'equilibrio economico.

Nella costruzione della teoria dell'equilibrio Pareto si scontrò con quella che ritenne una mancata corrispondenza tra teoria e fatti, e in particolare con quello che egli chiamò il "fenomeno soggettivo", cioè l'impatto sui comportamenti e quindi sui fenomeni sociali delle convinzioni soggettive, per irrazionali o false che esse possano essere. In definitiva, pur essendo molto più immerso di Walras nella problematica della matematizzazione dei processi reali, Pareto considerava tuttavia l'uso della matematica come un aspetto di un processo conoscitivo che deve essere saldamente radicato nel metodo sperimentale. Non essendo riuscito a dare un fondamento, un sostegno empirico alla teoria, Pareto entrò in quella crisi che lo spinse alla fine ad abbandonare il terreno dell'economia pura.

Della sua svolta vanno ricordati due aspetti: il distacco dalla razionalità come movente prevalente delle azioni umane e l'esigenza di ritrovare nel campo allargato della sociologia la verifica sperimentale che gli risultava impossibile trovare nell'ambito ristretto della teoria economica. Per il primo aspetto Pareto, che aveva introdotto il concetto di homo oeconomicus come astrazione analoga al 'punto materiale' in meccanica, giunse a collocare la razionalità in una posizione di secondo piano nella spiegazione dei moventi delle azioni umane, quei moventi che forniscono la chiave per interpretare i grandi fatti sociali. Costruì invece una teoria delle azioni 'non logiche', attribuendo a tali azioni un'importanza sempre maggiore per comprendere le regolarità del mondo sociale. Per il secondo aspetto, pur senza rinnegare la teoria dell'equilibrio economico generale, Pareto giunse a sottolinearne la limitatissima applicabilità a fini sia normativi sia descrittivi.

La povertà dei contenuti empirici della teoria era stata lamentata anche dai fisici e matematici in risposta ai tentativi di diffondere la teoria stessa fatti soprattutto da Walras (v. Ingrao e Israel, 1987, cap. 6). È questo il problema centrale che emerge dal carteggio tra Walras e Poincaré (sollecitato da Walras a dare il suo appoggio alla teoria): il problema che Poincaré solleva è appunto quello del procedimento di astrazione adottato nella costruzione della teoria e dei "giusti limiti" di questa procedura. Secondo Poincaré, "all'inizio di ogni speculazione matematica vi sono delle ipotesi e [...] affinché questa speculazione sia fruttuosa occorre (come nelle applicazioni alla fisica, del resto) che ci si renda conto di queste ipotesi. Se si dimenticasse questa condizione si supererebbero i giusti limiti". Anche il fisico matematico Paul Painlevé muove, nella sostanza, la stessa critica, nell'introduzione all'edizione francese del 1909 della Theory of political economy di Stanley William Jevons (1835-1882). Tale critica circola in molti ambienti di economisti, manifestandosi, in particolare, nel rifiuto da parte dell'ambiente di Cambridge di accettare la teoria in tutte le sue ambizioni di generalità e astrattezza.

Alle soglie degli anni trenta, dopo circa cinquant'anni di vita, la teoria walrasiana era ancora quasi inesplorata sotto il profilo matematico: il suo nucleo concettuale era già chiaramente espresso negli Eléments, ma esso non aveva ancora trovato una chiara definizione formale, in particolare attraverso una precisa e soddisfacente formulazione matematica dei problemi dell'esistenza, dell'unicità e della stabilità dinamica dell'equilibrio, né tanto meno erano stati conseguiti risultati concernenti tali problemi.

Ha inizio a questo punto quella che abbiamo indicato come la terza fase nello sviluppo storico della teoria e che è legata alla diffusione della modellizzazione matematica e quindi di un rapporto più elastico fra matematica e realtà, che non subisce in modo stretto i vincoli del riduzionismo meccanicista. Non a caso questa fase ebbe luogo in un diverso contesto geografico, trovando fertile terreno nei nuovi sviluppi assiomatici e astratti della scienza in Germania e in Austria. Questa nuova fase, legata soprattutto ai nomi di Abraham Wald (1902-1950) e John von Neumann (1903-1957), è caratterizzata da un cambiamento profondo dell'approccio matematico, che non è più quello dell'analisi infinitesimale, secondo le vedute della scuola di Losanna, bensì quello dell'analisi convessa. In verità i primi teoremi di esistenza dell'equilibrio, dimostrati da Wald nel quadro delle attività del Seminario Menger a Vienna, utilizzano ancora strumenti classici (ma con risultati limitati, proprio per le tecniche usate), mentre von Neumann apre la via, con l'uso delle tecniche di analisi convessa e dei teoremi di punto fisso, agli sviluppi che condurranno ai risultati degli anni cinquanta.

Questa fase (che è trattata in dettaglio in Ingrao e Israel, 1987, e in Weintraub, 1986) è tanto breve quanto decisiva per lo sviluppo della teoria e ha il suo culmine nel trattato scritto da von Neumann in collaborazione con Morgenstern (v. von Neumann e Morgenstern, 1944), in cui l'originale visione walrasiana viene rimpiazzata da una descrizione dei processi economici nel quadro della teoria dei giochi strategici. In tale impostazione l'adesione a un punto di vista modellistico astratto è la chiave che permetterà finalmente di tradurre il nucleo paradigmatico della teoria (le questioni dell'esistenza, dell'unicità e della stabilità dinamica dell'equilibrio) in una fruttuosa struttura matematica, ma implica anche un indebolimento dell'adesione al riduzionismo fisico-matematico classico. Ma soltanto in parte, perché più tardi la necessità di riferirsi - in assenza di altri validi riferimenti concettuali - al modello della fisica si presenterà ancora nel trattato di von Neumann e Morgenstern. L'asse appare tuttavia spostato dal riferimento alla fisica-matematica classica a quello allora dominante della fisica teorica, in pieno e impetuoso sviluppo.

La quarta fase può essere caratterizzata come quella in cui ha luogo la matematizzazione completa della teoria dell'equilibrio nella sua veste classica, entro un punto di vista assiomatico integrale di orientamento 'bourbakista': la sua più chiara manifestazione è la Theory of value di Debreu (v., 1959). Il primo periodo di questa fase si caratterizza per una prosecuzione del programma di uso sistematico della teoria dei giochi e dell'analisi convessa iniziato da von Neumann, che conduce, nel 1954, alla dimostrazione di un teorema molto generale di esistenza dell'equilibrio da parte di Kenneth Arrow e Debreu (entrambi nati nel 1921). Tuttavia, in questo lavoro di ricerca, il modello matematico viene man mano 'depurato' dei riferimenti alla teoria dei giochi attraverso un recupero dei concetti e del linguaggio della teoria walrasiana classica, sia pure entro il nuovo quadro formale e astratto. Tale impostazione ha consentito non soltanto di rispondere in modo positivo al problema dell'esistenza dell'equilibrio, ma anche di mostrare le insormontabili difficoltà che esistono sulla via di una dimostrazione della sua unicità.

In un secondo periodo, inaugurato dal contributo di Stephen Smale (nato nel 1930), si è avuto un ritorno ai metodi del calcolo differenziale classico, sia pure nell'ottica della moderna topologia differenziale: questo approccio ha consentito di ridimostrare tutti i risultati ottenuti in precedenza. In questa cornice differenziale è stato inoltre affrontato il problema della stabilità dinamica (e in particolare quello del tâtonnement) mostrando che, anche in questo ambito, è impossibile conseguire sul piano analitico i risultati sperati: i processi di aggiustamento dei prezzi non sono quasi mai convergenti, se non sotto ipotesi molto restrittive e di significato economico molto particolare.Questi risultati conducono allo stato presente della teoria e ai difficili problemi che essa è costretta ad affrontare per individuare possibili vie di sviluppo.

Il modello di Arrow e Debreu: l'equilibrio intertemporale con informazione perfetta

Ci proponiamo ora di fornire una sintesi molto semplificata della struttura del modello matematico dell'equilibrio economico generale, seguendo l'impostazione di Arrow e Debreu. A nostro avviso è del tutto legittimo scegliere il modello di Arrow e Debreu come riferimento fondamentale per dare un'immagine della struttura formale della teoria dell'equilibrio e per valutare i suoi risultati. Se è vero che il modello di Arrow e Debreu è diverso dalla costruzione di Walras, non è meno vero che la logica interna dello sviluppo della teoria porta in modo coerente dall'impostazione di Walras a quella dell'equilibrio intertemporale di Arrow e Debreu. Il modello di Arrow e Debreu può essere considerato un punto di arrivo dello sviluppo storico della teoria, che ne consente la 'radiografia' e una piena valutazione della coerenza fra intenti e risultati effettivamente conseguiti (per maggiori dettagli, v. Debreu, 1959).

Nel modello dell'equilibrio generale di Arrow e Debreu hanno un ruolo centrale i concetti di equilibrio, merci e prezzi. Del primo si è già detto. Le merci sono l'oggetto dell'attività economica, che consiste nella produzione e nello scambio di beni. La funzione dei prezzi è di operare come indicatori che informano gli agenti della scarsità dei beni.

Una merce è un bene o un servizio completamente specificato dai punti di vista fisico, spaziale e temporale, la cui quantità viene misurata mediante un numero reale e quindi con un punto x sulla retta dei numeri reali, IR. Se le merci presenti sul mercato sono in numero di n, un punto, o vettore, dello spazio cartesiano IRn delle n-ple di numeri reali indicherà la quantità in cui ciascuna delle merci è presente sul mercato. Tale vettore (x₁, ..., xn) sarà detto paniere di merci e può essere anche inteso come il piano d'azione di un agente economico, formulato ora per tutto l'orizzonte futuro (da cui il carattere deterministico del modello). IRn, ovvero lo spazio di tutte le possibili allocazioni (o panieri), sarà detto spazio delle merci.

A ogni merce è associato un numero reale, detto prezzo, che misura il suo 'valore' ovvero ciò che deve essere dato per ottenerla. Data la merce h, il numero ph indica il prezzo di un'unità di h, per cui data la quantità xh, il prezzo di xh è phxh. Dato un sistema di prezzi (p₁, ..., pn), il valore di un paniere di merci x=(x₁, ..., xn) è p₁x₁+...+pnxn=p·x.

Gli agenti economici si dividono in due categorie: i produttori e i consumatori. Il ruolo dei primi è di formulare un piano di produzione, mentre i secondi formulano un piano di consumo. Entrambi i piani sono espressi in termini di un paniere di merci; inoltre hanno validità illimitata, per cui la dinamica temporale è interamente conseguenza della scelta effettuata nel presente. Quest'ipotesi deterministica è giustificata dall'assunto che gli agenti abbiano una capacità di 'preveggenza illimitata'. L'altro postulato fondamentale è che gli agenti siano mossi dall'intento di realizzare il massimo vantaggio possibile, ovvero da un 'infinito egoismo'. L'attività di un consumatore è definita da due aspetti: le limitazioni fisiche e di mercato e i criteri di scelta del piano di consumo. Non tutti i piani sono, com'è ovvio, fisicamente possibili: quelli fisicamente possibili appartengono a un ben definito sottoinsieme di IRn, detto insieme di consumo. Non ci soffermeremo sulle ipotesi matematiche che permettono di caratterizzare gli insiemi di consumo.

La descrizione matematica dei criteri di scelta si consegue ammettendo che il consumatore i, di fronte a due panieri x e y, sia in grado di decidere quale preferisce. Si scriverà x≺y per indicare che i preferisce y a x, xĩy per indicare che x e y sono equivalenti per i e x≾_iy per indicare che y è preferibile o equivalente a x per ĩ. È facile constatare che la relazione i è riflessiva e transitiva ma non antisimmetrica (come lo sono le relazioni d'ordine), mentre ĩ è una relazione d'equivalenza. Le classi di equivalenza rispetto alla relazione d'indifferenza ĩ si dicono classi d'indifferenza e curve d'indifferenza se si riducono a curve. Si possono fare numerose ipotesi circa le relazioni di preferenza. La più famosa è l'ipotesi di convessità forte, che si esprime dicendo che, se xĩy, allora tx+(1-t)y≻_ix(0<t<1), ovvero che, se x è indifferente a y per i, allora questi preferisce a entrambi una media ponderata di essi. Non è difficile constatare che tale ipotesi implica il fatto che le curve d'indifferenza siano convesse, il che semplifica molte dimostrazioni.

L'ipotesi di 'infinito egoismo' si traduce asserendo che non sono possibili 'consumi di sazietà' per il consumatore, ovvero che non esistono panieri tali che non ne esistano altri ad essi preferibili.Passiamo ora all'introduzione dei vincoli di mercato. Si assume che all'inizio dell'attività economica il consumatore i possieda una certa 'ricchezza', espressa in termini di un paniere di merci ('risorse iniziali'): ωi=(ωi₁, ..., ωin). Il valore di ωi (o 'ricchezza' di i) è determinato dal vettore di prezzi p vigente sul mercato ed è quindi

Dato un vettore di prezzi p, l'agente i selezionerà un piano di consumo 'ammissibile', rappresentato da un vettore xi, il cui valore non potrà superare la sua ricchezza, cioè tale che p·xi≤p·ωi=wi.

L'insieme di queste scelte ammissibili γi(p, wi)={xi|p·xi≤wi} è detto insieme di bilancio. L'iperpiano p·xi=wi è detto vincolo di bilancio di i. A causa dell'ipotesi di 'insaziabilità', i sceglierà un paniere appartenente a tale vincolo e all'insieme di preferenza 'migliore' per lui. In termini matematici questa scelta xi dovrà essere massimale rispetto alla relazione ≾_i.

Resta così definita una corrispondenza ξi che associa al prezzo di mercato p e alla ricchezza wi di i un insieme ξi(p, wi) di piani di consumo, detto insieme di domanda. Tale corrispondenza non è in generale una funzione univoca: lo è se la relazione ≾_i è fortemente convessa; ove si faccia a meno di questa ipotesi restrittiva è quindi necessario far ricorso alla complessa teoria delle funzioni multivoche.

Passiamo ora al settore della produzione. Come si è visto, il compito del produttore j sarà quello di formulare un piano di produzione espresso mediante un paniere di merci yj (vettore di IRn). La scelta dei piani di produzione è limitata da vincoli fisici e tecnologici. Dato un vettore di prezzi p e un piano di produzione yj=(yj₁,...,yjn), la quantità

è detta profitto di j e la denoteremo con πj(p). Il produttore cercherà di ottenere il massimo profitto possibile al dato prezzo p; resterà così definita una funzione (in generale multivoca) ηj che associa a ogni vettore dei prezzi p l'insieme ηj(p) delle produzioni che massimizzano il profitto di j e che sarà detta corrispondenza di produzione.

Possiamo ora dare la definizione formale di un'economia. Essa è definita dagli elementi seguenti.

1. Sono dati r consumatori e s produttori, cioè r+s agenti che operano sul mercato.

2. Per ogni consumatore i (i=1,...,r) sono definiti i vincoli fisici delle sue attività e la relazione di preferenza ≾_i.

3. Per ogni produttore j (j=1,...,s) sono definiti i vincoli tecnologici delle sue attività.

4. Per ogni consumatore i è dato l'insieme delle risorse iniziali ωi=(ωi₁,...,ωin).

Si noti ora che le risorse iniziali dell'intera economia in termini della merce t (t=1,...,n) sono date dalla somma

,

per cui il vettore ω=(ω₁,...,ωn) { IRn sarà il vettore delle risorse iniziali dell'economia. Uno stato dell'economia è definito da un piano di consumo completo per ogni consumatore e un piano di produzione completo per ogni produttore, cioè da una (r+s)-pla di vettori di IRn: (x¹ ,..., xr, y¹ ,..., ys)=(x, y). Dato un siffatto stato dell'economia, il vettore

è la domanda totale netta. Sottraendo le risorse iniziali ω del sistema da questo vettore, si ottiene un vettore che misura la differenza fra domanda e offerta in tutti i mercati dell'economia. Tale vettore viene detto eccesso di domanda: z=x-y-ω.

Se z=O e quindi x-y=ω, per ogni bene la domanda netta del mercato eguaglia le risorse iniziali totali; in questo caso lo stato (x, y) viene detto equilibrio di mercato.

Il contesto in cui viene di solito esaminato il problema dell'equilibrio è quello delle cosiddette economie con proprietà privata delle risorse. In esse il consumatore i possiede non soltanto ωi, ma anche una quota dei profitti dei produttori. La frazione posseduta da i del profitto πi di j è un numero compreso fra 0 e 1 che denoteremo con Θij (ovviamente formula).

In corrispondenza del vettore dei prezzi p, la ricchezza di i è data dal valore delle sue risorse iniziali e dalla sua quota di profitto, ovvero da

In un'economia con proprietà privata delle risorse, un equilibrio di mercato è una (r+s+1)-pla di punti di IRn,(x*, y*, p*)=(x(¹)*, x(²)* ,..., x(r)*, y(¹)*, ..., y(s)*, p*), tale che:

a) nell'insieme dei panieri x(i) il cui valore non supera il vincolo di bilancio, cioè tali che

è massimale rispetto a ≾_i;

b) y(j)* massimizza il profitto rispetto al prezzo p*;

c) x*-y*=ω.p* sarà detto vettore di prezzi di equilibrio.

Dato il vettore dei prezzi p, i sceglie xi nell'insieme di domanda

In un'economia con proprietà privata delle risorse ξi dipende soltanto da p e quindi possiamo scrivere ξi(p). La somma delle domande individuali fornisce la domanda totale

,

che definisce la corrispondenza di domanda totale

Analogamente si definisce la corrispondenza di produzione totale

,

tale che

Consideriamo ora l'insieme dei vettori ottenuti sottraendo l'offerta dalla domanda, ovvero ξ(p)-η(p)- +ω=ζ(p). L'eccesso di domanda z=x-y-ω è un vettore di questo insieme ζ(p). Resta così definita la corrispondenza (in generale multivoca) ζ:→ζ(π)= ξ(p)-η(p)-ω, che viene detta corrispondenza di eccesso di domanda dell'economia.

Risolvere il problema dell'esistenza dell'equilibrio significa dimostrare che esiste almeno un vettore di prezzi di equilibrio p*, cioè un vettore p* tale che ζ(p*) contenga il vettore nullo. In formule il problema è: esiste un p* tale che 0{ζ(p*)? Se esiste un siffatto p* cercheremo successivamente di vedere se esso è unico.

Il problema è assai più semplice se ζ è una funzione univoca, poiché allora ζ(p) si riduce a un solo elemento e si tratta di vedere se esiste un vettore di prezzi p* tale che ζ(p*)=0, ovvero se l'equazione ζ(p)=0 ammette una soluzione, e se tale soluzione è unica.

Accenniamo ora al modo in cui si formalizza il problema della stabilità globale o dinamica dell'equilibrio, limitandoci a tradurre matematicamente il cosiddetto processo di tâtonnement.

Si suppone che esista un agente esterno al mercato chiamato 'banditore' che ha le funzioni di informazione e di coordinamento. La prima funzione consiste nell'informare gli agenti economici dei prezzi delle merci, ovvero nell''annunciare' un vettore di prezzi p(¹)=(p(¹)₁ ,..., p(¹)n). Questa informazione è la base per la determinazione dei piani di consumo e di produzione e quindi delle funzioni ξ(p(¹)) e η(p(¹)). La seconda funzione del banditore consiste nel calcolo dell'eccesso di domanda ζ(p(¹)). Se p(¹) è un vettore di prezzi di equilibrio, gli scambi e la produzione sono possibili; altrimenti il banditore 'griderà' un nuovo vettore di prezzi p(²). Il processo iterativo continuerà finché non sia stato raggiunto un vettore di prezzi di equilibrio. Si noti che il vettore di prezzi p(i) viene cambiato dal banditore secondo una legge che dovrà essere ben definita e che gli agenti economici potranno operare soltanto se p(i) è un vettore di prezzi di equilibrio.

La legge di aggiustamento dei prezzi scelta da Walras riflette la cosiddetta 'legge della domanda e dell'offerta': se l'eccesso di domanda di una merce k è positivo, il prezzo di k cresce, se è negativo, il prezzo di k decresce. Se ora consideriamo il vettore dei prezzi p come funzione p(t)=(p₁(t), ..., pn(t)) del tempo t, l'ipotesi che pk(t) sia crescente si esprime matematicamente dicendo che la derivata di pk(t) rispetto al tempo è positiva. In simboli:

Analogamente, se pk(t) è decrescente,

Il fatto che una crescita (o una decrescita) di pk(t) corrisponde alla positività (o alla negatività) dell'eccesso di domanda si può esprimere asserendo che p·k(t) è proporzionale a ζi(p), cioè: p·k(t)=αϰζk(p), dove ak è un numero reale positivo. Otteniamo così il sistema di equazioni differenziali che descrive il tâtonnement:

Le soluzioni di questo sistema sono date da un sistema di n funzioni: p₁=p₁(t), p₂=p₂(t), ..., pn=pn(t). I vettori di prezzi di equilibrio sono le soluzioni costanti.

Il problema della stabilità globale ha pertanto la seguente traduzione formale: dato un processo di tâtonnement, descritto dalle funzioni p₁=p₁(t), ..., pn=pn(t), che non parta da uno stato di equilibrio, è vero oppure no che esso tende verso un vettore di prezzi di equilibrio? Se ciò è vero quale che sia il vettore di prezzi da cui ha inizio il tâtonnement, allora vuol dire che le forze operanti nel mercato sono capaci di guidare il sistema verso uno stato di compatibilità delle azioni indipendenti.

Una valutazione critica del modello di Arrow e Debreu: struttura, risultati analitici, interpretazioni, sviluppi recenti

Se si vuole dare una valutazione critica del modello di Arrow e Debreu e, più in generale, del programma di ricerca sull'equilibrio economico generale, occorre partire dalla considerazione che vi è un'unità sostanziale tra le questioni storiografiche, i problemi e i risultati matematici. Questa unità è stata troppo spesso trascurata o dimenticata sia nella storiografia del pensiero economico, sia nel dibattito teorico sull'equilibrio economico generale.

La storia della teoria illumina in modo penetrante le finalità che hanno guidato la sua costruzione ed è quindi un elemento essenziale per capire perché essa sia giunta a porsi determinati problemi formali. La riflessione sui problemi matematici offre una chiave importante per valutare i successi e gli insuccessi della teoria, anche sulla base dei criteri interni di scientificità che il programma di ricerca sull'equilibrio economico generale si è dato nell'arco della sua lunga evoluzione.

Abbiamo sottolineato come il modello scientifico dei teorici dell'equilibrio generale sia stato quello della fisica matematica classica; questa osservazione apre molti problemi nuovi, sia nella storia che nella valutazione dello stato della teoria, i quali possono essere riassunti in una serie di quesiti che hanno trovato prime significative risposte in diverse opere citate nella bibliografia. Quali sono stati i paradigmi di riferimento presi a prestito dalle scienze fisico-matematiche e perché essi hanno avuto un ruolo così importante nella costruzione della struttura formale della teoria? Quali problemi si sono posti nel trasferimento di quei paradigmi dal contesto delle scienze fisico-matematiche a quello dei fenomeni di mercato e come si è tentato di affrontarli e risolverli? Quali sono stati i canali di comunicazione tra il mondo scientifico e gli studiosi impegnati sulla frontiera della matematizzazione della scienza sociale? (È fuor di dubbio, infatti, che la teoria dell'equilibrio economico generale sia stata, fino a un'epoca recentissima, la frontiera della matematizzazione della scienza sociale). In che modo si sono sviluppati questi canali di comunicazione e che ruolo ha avuto il dialogo con i fisici matematici nella costruzione della teoria? Infine in quale misura e in quali periodi i fisici matematici si sono rifiutati di dare un contributo al progetto di matematizzazione perseguito dai teorici dell'equilibrio economico generale?

Si tratta di quesiti che portano a riflettere sulle ambizioni e le conquiste, reali o presunte, della teoria dell'equilibrio economico generale e impongono di verificare se i risultati ottenuti nella lunga evoluzione della teoria siano stati effettivamente all'altezza delle ambizioni di 'scientificità' che ne hanno costantemente ispirato la costruzione. L'assiomatizzazione della teoria completata negli anni cinquanta ha svolto un ruolo fondamentale per quest'opera di chiarificazione, forse più di quanto non sia stato riconosciuto finora, e ciò conferma il ruolo centrale che ha avuto sul piano analitico il modello di Arrow e Debreu.

Il problema che è al cuore della valutazione della teoria può essere formulato come segue. Nell'opera di Walras e di Pareto prende forma un nucleo di problemi analitici che si conserva come nucleo centrale di tutte le successive versioni della teoria. Si tratta dei tre problemi dell'esistenza, dell'unicità e della stabilità globale dell'equilibrio, in un mercato di concorrenza perfetta dove gli agenti razionali siano price-takers e la compatibilità delle decisioni indipendenti degli agenti sia assicurata da un sistema di prezzi intesi come segnali. La dimostrazione matematica dell'esistenza dell'equilibrio è la risposta formale al problema della coerenza e della compatibilità dei fini, dati i vincoli della tecnologia e delle risorse. La dimostrazione matematica dell'unicità dell'equilibrio è la condizione perché abbia significato il confronto tra diversi stati di equilibrio dell'economia al variare dei vincoli o delle preferenze (statica comparata). Infine la dimostrazione della stabilità globale ha come scopo quello di mostrare come, sia pure in condizioni ideali e astratte, il meccanismo di mercato guidato dalla 'mano invisibile' dei prezzi converga verso lo stato di equilibrio.

Anche al di là dei problemi interpretativi e di 'realismo' della teoria, assai dibattuti nel corso della sua storia, l'assiomatizzazione ha portato alla luce le gravissime difficoltà interne allo stesso nucleo centrale della teoria: i due problemi dell'unicità dell'equilibrio e della stabilità globale del tâtonnement non soltanto sono rimasti irrisolti, ma appaiono insolubili entro la struttura formale della teoria. L'assiomatizzazione ha avuto l'importante funzione di evidenziare questa difficoltà analitica. Restano da valutare le conseguenze di questo fallimento sull'intero programma di ricerca sull'equilibrio economico generale.

Non è possibile, entro i limiti di questo articolo, presentare una rassegna esauriente dei risultati ottenuti sul piano matematico: ci limiteremo ad alcuni cenni rinviando a Ingrao e Israel (v., 1987) e a Weintraub (v., 1986) per maggiori dettagli.

Come si è già detto, il teorema di esistenza dell'equilibrio è senz'altro il risultato più rilevante e significativo della teoria. L'esistenza dell'equilibrio economico fu infatti dimostrata da Arrow e Debreu (nel 1954) sotto ipotesi assai poco restrittive: per l'eccesso di domanda ζ(p) si richiede soltanto che sia una corrispondenza (e quindi non necessariamente univoca) semicontinua superiormente. Il teorema di Arrow e Debreu costituisce il culmine di una serie di ricerche iniziate da von Neumann e pone al centro l'uso dei teoremi di punto fisso. Numerose generalizzazioni di questo teorema furono ottenute in seguito (fra le quali va menzionata quella dovuta ad A. Mas Colell).

Quanto all'unicità dell'equilibrio, fu quasi subito evidente che era facile produrre esempi di economie con più di un equilibrio. Restava aperto il problema di determinare le condizioni sotto le quali l'unicità si verificava. La ricerca svolta a partire dagli anni cinquanta ha dimostrato che non si riesce a dimostrare l'unicità dell'equilibrio, così come non si riesce a dimostrare la convergenza del tâtonnement, se non in circostanze molto particolari come quella in cui tutte le merci sono 'sostituti'. In una serie di lavori iniziati nel 1976 Debreu analizzò a fondo la questione dell'unicità, mostrando non soltanto che essa in generale non è verificata, ma anche che gli equilibri possono essere in numero infinito. L'unica limitazione significativa (ed è questo il principale risultato di Debreu al riguardo) è che l'insieme delle economie che hanno un numero discreto di equilibri è 'generico', ovvero che le economie sono 'quasi tutte' di questo tipo.

La questione della convergenza del tâtonnement fu affrontata agli inizi degli anni cinquanta con alterni risultati, fino a che, nel 1960, Herbert Scarf non produsse esempi di economie globalmente instabili. Questa scoperta arrestò le ricerche per un lungo periodo fino a che, negli anni settanta, Stephen Smale tentò di superare la difficoltà proponendo un processo di aggiustamento dei prezzi diverso dal tâtonnement, che costituisce una generalizzazione 'globale' del classico metodo di Newton per il calcolo degli zeri: tale processo è convergente, al prezzo tuttavia di alcune ipotesi ineliminabili (come una forte restrizione degli stati iniziali ammissibili del processo medesimo) e di una difficoltà di interpretazione economica. Analisi successive hanno mostrato che il processo di Smale non può essere migliorato e che esso resta soprattutto un efficace e interessante strumento di carattere puramente matematico per la determinazione numerica di equilibri di un campo vettoriale.

Le difficoltà inerenti alle questioni dell'unicità e della stabilità sono legate a un difetto di specificazione delle ipotesi di base del modello e della forma delle funzioni eccesso di domanda aggregate. In termini più precisi il problema centrale è che la procedura di formazione dell'eccesso di domanda attraverso l'aggregazione delle domande individuali (a loro volta derivanti dalla struttura delle relazioni di preferenza) non lascia traccia della struttura di tali funzioni (le domande individuali) nella forma della funzione eccesso di domanda aggregata, la quale si presenta come una funzione quasi del tutto generica. Ciò è stato mostrato da Hugo Sonnenschein nel 1974 con un teorema dal quale risulta che ogni funzione polinominale può essere pensata come funzione eccesso di domanda ζ(p) di un'economia e quindi (a norma di un classico teorema di approssimazione di Weierstrass) che ogni funzione continua è una funzione eccesso di domanda. Il teorema di Sonnenschein illustra meglio di qualsiasi altro risultato il vizio di fondo della teoria: quanto sia illusoria la speranza di conseguire risultati così stringenti come l'unicità e la stabilità nel caso di una funzione eccesso di domanda praticamente arbitraria.Il giudizio di sintesi è che la teoria dell'equilibrio economico generale giunge a una incoerenza tra le proprie finalità e i risultati analitici ottenuti: sulla base delle premesse del modello assiomatizzato neowalrasiano di Arrow e Debreu non è possibile dedurre in modo rigoroso quei risultati (stabilità globale e unicità dell'equilibrio) che pure sono un elemento centrale del nucleo paradigmatico della teoria.

È certamente legittimo chiedersi se la teoria dell'equilibrio economico generale possa fare a meno dei risultati di stabilità globale e unicità e, in particolare, se il tâtonnement sia davvero così importante per essa o sia soltanto un espediente di Walras, di cui è possibile sbarazzarsi senza troppe angustie. È tuttavia evidente come il fatto che i casi in cui l'equilibrio non è unico siano la quasi totalità sia di per sé un ostacolo grave a ogni tentativo applicativo e, più in generale, a ogni tentativo di ricavare dalla teoria dei significativi teoremi di statica comparata. È inoltre agevole constatare che non è affatto facile espungere la tematica della stabilità globale dal quadro walrasiano e neppure dal quadro assiomatizzato neowalrasiano.

Espungere questa tematica significherebbe riproporre una lettura totalmente normativa della teoria dell'equilibrio economico generale: ciò è stato di fatto tentato e il filone algoritmico inaugurato da Scarf, che studia il calcolo degli equilibri in modelli di equilibrio applicati, elaborati per condurre valutazioni di politica economica (v. Scarf, 1973), si è mosso proprio in questa direzione. Questo nuovo indirizzo della ricerca è una riscoperta dell'anima normativa della teoria, che lascia tuttavia irrisolta la conciliazione con le finalità descrittive della teoria. La grande difficoltà è il paradosso di una teoria normativa dell'economia di mercato, che rinuncia alla dimostrazione dell'efficacia spontanea del libero mercato e giunge così a una equivalenza con la teoria della pianificazione. Anche una teoria normativa dell'equilibrio, se non vuol rinunciare a essere una teoria del mercato oltre che una teoria dell'equilibrio, non può prescindere dalla decentralizzazione delle decisioni e delle scelte e quindi da un meccanismo spontaneo che nello scambio guidi le decisioni indipendenti a convergere verso la compatibilità nello stato di equilibrio. È certamente legittimo criticare l'inadeguatezza della descrizione dei processi di aggiustamento dei prezzi mediante il tâtonnement; ma, pur prescindendo dal fatto che la ricerca di altri tipi di processi aventi caratteristiche di convergenza ha dato risultati assai modesti e pochissime speranze di conseguire miglioramenti, è paradossale pensare che si possa costruire una teoria normativa del libero mercato senza libero mercato e cioè sul solo presupposto di un algoritmo di calcolo scelto per motivi di convenienza matematica dagli specialisti del settore. In conclusione la convivenza precaria tra l'anima normativa e l'anima descrittiva attraversa tutta la storia della teoria dell'equilibrio economico generale, fino ai problemi aperti sulla frontiera della ricerca attuale.

Le considerazioni precedenti conducono al quesito se il quadro assiomatico classico della teoria (e in particolare la sua espressione più compiuta, ovvero il modello di Arrow e Debreu) debba ancora essere considerato centrale oppure si possa configurare un suo abbandono, nella speranza di non incontrare, in nuovi contesti, analoghi problemi di coerenza tra premesse e risultati analitici, o addirittura di risolvere i problemi di indeterminatezza e di povertà di risultati che sorgono entro il quadro classico. Tuttavia, quando si esce dal quadro delle ipotesi alla Arrow-Debreu, si apre un vaso di Pandora: i problemi delle aspettative, dell'incertezza e del tempo, liberati dalla costrizione forzosa entro lo schema artificioso della perfetta preveggenza e dell'economia di mercati futuri completi, generano scompiglio, distruggono le pretese di imitazione dei modelli fisici e obbligano a rimettere in discussione radicalmente la metodologia stessa dell'equilibrio.

La letteratura recente ha sottoposto a revisione l'una o l'altra delle ipotesi nel tentativo di dilatare la struttura di base del modello assiomatico, abbandonando i tratti più artificiosi e irrealistici della teoria. Tre indirizzi di ricerca hanno perseguito questo obiettivo, accantonando i requisiti della stabilità e dell'unicità dell'equilibrio, come se tali requisiti non fossero essenziali al significato e alla validità della teoria, e rinunciando persino alla pretesa di pervenire alla dimostrazione di teoremi di esistenza sotto condizioni generali.Il primo indirizzo di ricerca ha prodotto modelli di equilibrio generale abbandonando l'ipotesi della concorrenza perfetta nell'ambito della produzione, vale a dire l'ipotesi classica che i produttori assumano come dati i prezzi di mercato. Come abbiamo visto, tale ipotesi comporta l'artificiosa presenza di un 'banditore', poiché nessuna delle imprese presenti sul mercato ha la capacità di definire i prezzi di vendita. I modelli di equilibrio con concorrenza monopolistica impostano nel contesto dell'equilibrio generale il problema della concorrenza monopolistica definito dall'economista statunitense Edward Hastings Chamberlin (v., 1933). La concorrenza monopolistica è quella forma di mercato che si ha quando numerose imprese di piccole dimensioni, in condizioni di libertà di entrata sul mercato, offrono prodotti differenziati che sono sostituti nelle funzioni di domanda dei consumatori.

Molte difficoltà sorgono nel trasferire questo impianto entro un modello alla Arrow-Debreu. Come definire la libertà di entrata, se imprese e beni sono in numero dato? Come inserire allora la differenziazione dei prodotti e la loro sostituibilità? Come far intervenire le curve di domanda dei prodotti differenziati nelle scelte di ciascuna impresa?Nei modelli di equilibrio generale con concorrenza monopolistica elaborati nella letteratura recente le imprese sono in numero dato, ma hanno il potere di fissare il prezzo del proprio prodotto, tenendo conto della curva di domanda (la relazione tra prezzo e quantità domandata) per ciascuna impresa. In una classe di modelli le imprese effettuano le proprie scelte congetturando la curva di domanda che limita il loro operare sul mercato, sotto la condizione aggiuntiva, tuttavia, che le loro congetture siano corrette almeno in corrispondenza della soluzione di equilibrio, vale a dire che le curve di domanda soggettivamente percepite come vincoli dalle imprese passino per il punto di equilibrio quale risulta dalla soluzione del modello.

Questa impostazione è stata proposta da Negishi (v., 1961) e ripresa dallo stesso Arrow (v., 1971) in un celebre articolo sul ruolo dell'impresa nei modelli dell'equilibrio economico generale. È possibile dimostrare teoremi di esistenza dell'equilibrio anche per questi modelli, ma sotto ipotesi più restrittive di quelle del modello dell'equilibrio generale di concorrenza perfetta.

Le curve di domanda così inserite nel modello sono arbitrarie, perché rappresentano le aspettative soggettive delle singole imprese, senza una teoria che si proponga di darne conto. Sulla spiegazione teorica prevale allora la convenienza analitica: così, ad esempio, alle funzioni che rappresentano le aspettative delle imprese circa la relazione tra prezzi e quantità domandate sul mercato del loro prodotto si attribuisce a priori una certa forma per facilitare la ricerca di soluzioni. Per rimuovere tale arbitrarietà, in altre famiglie di modelli si è seguita la via di costruire curve di domanda oggettive, che riflettono non ipotesi arbitrarie formulate dalle imprese, ma le relazioni tra prezzi e quantità sui mercati descritti dalla teoria. Si immagina allora che ciascuna impresa compia le scelte di produzione (con l'obiettivo del massimo profitto) assumendo come date le scelte delle altre imprese e prevedendo esattamente gli effetti sul vettore dei prezzi di mercato di tutte le scelte di offerta. In questo contesto la dimostrazione dell'esistenza dell'equilibrio è però problematica e sono stati presentati controesempi di modelli che non ammettono soluzioni (v. Roberts e Sonnenschein, 1977).

Nei modelli di cui si è detto, come nell'originario modello di Chamberlin, non c'è interazione strategica tra le imprese: le imprese non scontano le reazioni delle imprese concorrenti alle decisioni assunte su prezzi o quantità prodotte, ma si limitano a prendere atto delle scelte effettuate dalle altre imprese per quel tanto che tali scelte si rivelano nei dati aggregati del mercato. In un'altra classe di modelli, al contrario, si esamina il problema della concorrenza imperfetta a partire dalla teoria dei giochi, strumento teorico per rappresentare le situazioni di interazione strategica, nelle quali ciascun soggetto che assume decisioni è consapevole della capacità degli 'avversari' di rispondere con mosse razionali alle sue strategie di gioco.

Un secondo indirizzo di ricerca che si muove nella scia della definizione di concorrenza perfetta elaborata da Cournot mira a dimostrare che l'equilibrio di una economia di molti produttori tende al limite all'equilibrio walrasiano (v. Hildenbrand, 1973).

In sintesi, l'abbandono dell'ipotesi della concorrenza perfetta apre la difficile alternativa tra modelli che precipitano in rappresentazioni arbitrarie delle aspettative e modelli che, costruiti su premesse di coerenza e oggettività più solide, non possono però raggiungere risultati analitici forti per la complessità delle interazioni possibili tra gli agenti. Della stessa natura, ma molto maggiori, sono le difficoltà che si incontrano quando si tenta di adattare lo schema dell'equilibrio generale alla Arrow-Debreu per rimuovere le fantasiose ipotesi sulla struttura degli scambi nel tempo. I tentativi in questa direzione, fondati sulla ripresa del concetto di equilibrio temporaneo, sono approdati a sofisticati modelli di economie sequenziali con previsione perfetta.

Questo terzo filone di ricerca è stato inaugurato negli anni settanta soprattutto da J.M. Grandmont e poi è stato sviluppato dallo stesso Grandmont e da numerosi altri studiosi, fra cui vanno segnalati Y. Younès, F. Fuchs, G. Laroque, J.P. Benassy (per un'ampia rassegna, v. Grandmont, 1988).

I modelli di equilibrio temporaneo più esplorati nella letteratura sono modelli a generazioni sovrapposte: non si considera più una data finale degli scambi, un orizzonte finito dei piani e delle transazioni progettate e decise nell'istante iniziale, ma un orizzonte infinito, perché nei mercati si succedono, sovrapponendosi, generazioni di agenti economici, ciascuna delle quali ha un orizzonte di vita finito. Poiché gli scambi continuano in un futuro indefinito (ogni generazione muore, ma lascia spazio alla generazione divenuta adulta, che a sua volta convive con la generazione più giovane), i mercati hanno un numero infinito di merci e di agenti. Infinite sono le date alle quali potranno essere disponibili i diversi beni.

Una delle motivazioni principali di queste ricerche è legata alla critica dell'ipotesi che gli agenti economici siano illimitatamente preveggenti e del carattere statico della 'dinamica' che essa comporta. Per superare questo inconveniente si postula che i mercati si succedano nel tempo e che gli agenti economici apprendano soltanto in modo graduale le leggi dinamiche dell'economia in cui operano. Per dare un'idea di tale approccio, consideriamo un caso elementare. In coerenza con quanto detto, supporremo che l'equilibrio al tempo t sia completamente determinato dalle previsioni fatte, allo stesso tempo t, dagli m agenti economici, circa lo stato in cui l'economia si troverà nell'immediato futuro t+1: indichiamo con χi,e t+₁ tali previsioni per l'agente i-esimo. Allora l'equilibrio sarà dato dall'equazione funzionale dove f descrive il risultato del processo di aggiustamento verso l'equilibrio del mercato per un dato sistema di aspettative.

L'equilibrio intertemporale è allora definito come una sequenza di stati ⟨xt> e di previsioni ⟨xi, et+₁ > tali che sia soddisfatta l'equazione dell'equilibrio (*) e si abbia xi, et+₁=xt+₁ per ogni i e ogni t.

L'informazione di ogni agente al tempo t è descritta dalla sequenza (xt, xt-₁, ...). Quindi le relazioni di previsione sono date da: dove ψi sono le funzioni di aspettativa. Le equazioni dell'equilibrio di mercato si scriveranno allora: La dinamica di un'economia è così descritta, date le f e le ψi, come una sequenza di equilibri temporanei che hanno luogo ricorsivamente nel tempo.

L'approccio degli equilibri temporanei è stato applicato anche al di fuori della cornice classica, abbandonando l'ipotesi di piena occupazione, e ha permesso di toccare questioni come quella della struttura dei modelli macroeconomici keynesiani della disoccupazione o quella dei fondamenti microeconomici della teoria monetaria. In alcuni modelli di equilibrio temporaneo si è tentato di inserire la moneta e di analizzarne il ruolo come mezzo di scambio. Inoltre la teoria si è sviluppata sia nel quadro deterministico che in quello stocastico.

Problemi centrali di questa teoria, sul piano analitico, sono la dimostrazione dell'esistenza dell'equilibrio nel breve periodo e della stabilità del medesimo sul lungo periodo. Occorre tuttavia osservare che, probabilmente a causa della sua notevole complessità matematica, questa teoria si presenta con caratteristiche molto più frammentate di quella classica ed è assai meno accentrata attorno a risultati generali. Lo stesso Grandmont ha recentemente osservato (v. Grandmont, 1988) che molto si deve ancora fare per ottenere in questo contesto formulazioni e risultati generali e compatti. Particolarmente critico è ancora il livello dei risultati ottenuti attorno al problema centrale della stabilità dell'equilibrio di lungo periodo. Al di là dei risultati formali conseguiti e ancora aperti, non appare risolto e neppure affrontato in termini davvero innovativi il problema di costruire dei modelli che contengano una descrizione effettivamente dinamica dei processi di mercato, come gli stessi autori ammettono. In conclusione, ancora una volta, il problema che ha ispirato questo sviluppo si ripresenta in forma sostanzialmente irrisolta.In tema di dinamica, un dibattito si è sviluppato sul modello walrasiano con accumulazione di capitale, quel modello che secondo gli intenti di Walras doveva estendere la teoria dell'equilibrio generale al caso di mercati dove gli agenti risparmiano e le imprese offrono nuovi beni capitali, cioè a una rappresentazione schematica del processo di accumulazione e crescita in condizioni di concorrenza perfetta. Questo modello walrasiano, che ipotizza un saggio di rendimento uniforme per tutti i beni capitali di nuova produzione, ammette soluzioni solo sotto l'ipotesi che in equilibrio la produzione di alcuni beni capitali possa essere nulla. Questo risultato formale ha suscitato controverse interpretazioni. Secondo alcuni studiosi, ciò comporta una radicale inadeguatezza del modello walrasiano con accumulazione di capitale, che non potrebbe dar conto in modo coerente di un equilibrio con accumulazione di capitale nel lungo periodo, perché non garantirebbe simultaneamente la condizione di uniformità del saggio di profitto e la riproduzione di tutti i beni capitali. Secondo altri interpreti, tuttavia, non era intento di Walras comprimere il processo di accumulazione entro lo schema di un equilibrio di lungo periodo. Questi interpreti, più attenti alla lettura del testo walrasiano, sottolineano piuttosto come, pur nelle residue ambiguità del modello, la struttura proposta da Walras anticipi un modello di equilibrio temporaneo, una successione di equilibri nel tempo con ipotesi molto semplici sulla formazione delle aspettative. La difficoltà maggiore della originaria teoria walrasiana in tema di dinamica resta invece l'impossibilità di dar conto del mutamento dei dati (preferenze, tecnologia, risorse) e di conciliare, in un'unica struttura teorica, questi mutamenti di struttura con i processi di aggiustamento dei prezzi.

Conclusioni

La ricca e tormentata storia della teoria dell'equilibrio economico generale conduce ad alcune significative riflessioni.La prima riflessione riguarda l'enorme ambizione e forse l'ingenuità con cui è stato affrontato il problema dell'equilibrio generale del mercato. In un carteggio con Pietro Verri, nel 1773, Condorcet metteva in guardia Verri dal sottovalutare le difficoltà della formalizzazione nella scienza sociale, osservando che le maggiori menti matematiche dell'epoca non erano state in grado di risolvere il 'problema dei tre corpi', e commentava: "Essi suppongono che questi corpi siano delle masse senza estensione [...] e questo problema, benché limitato da cento condizioni che lo facilitano, li ha occupati da venticinque anni e li occupa ancora. L'effetto delle forze che agiscono nella testa del commerciante, anche il più stupido, è ben più difficile da calcolare". Una problematica analoga, anche se affrontata in un'ottica diversa, emerse nel carteggio tra Walras e Poincaré: Poincaré sosteneva che fosse lecito assumere come punto di partenza una grandezza non misurabile (l'utilità espressa con una funzione arbitraria), ma non certo che una teoria costituita su queste basi fosse soddisfacente. Pur senza approfondirlo, Poincaré aveva toccato con grande acume un problema cruciale della teoria: il difetto di specificazione dovuto all'elevato numero di funzioni arbitrarie incluse nelle sue premesse.Tutte queste difficoltà acquistano un pieno significato se sono viste nel contesto del problema generale delle difficoltà che insorgono, in forme ormai ben note, quando si tenta di matematizzare dei campi di fenomeni ben più complessi di quelli fisici, quali sono i fenomeni biologici e sociali.

Un secondo ordine di riflessioni investe l'ipotesi che è a fondamento della descrizione del comportamento degli agenti economici nei modelli di equilibrio: l'idea che gli agenti economici sono razionali in un senso molto particolare, cioè sono capaci di scegliere in modo coerente secondo procedure di ottimizzazione, dati i segnali che ricevono dal mercato. Questa visione della razionalità individuale del consumatore è controversa e criticabile, poiché attribuisce agli individui capacità di calcolo esagerate, mentre omette di rappresentare quella più autentica razionalità, essenziale anche nell'attività economica, che è la capacità inventiva e più in generale la capacità di interagire in modo creativo con l'ambiente. Gli agenti dei modelli di equilibrio economico generale sono degli "idioti razionali", come li ha spiritosamente definiti l'economista Amartya Kumar Sen. I risultati della storia della teoria dell'equilibrio economico generale mostrano che l'ipotesi della razionalità individuale del consumatore, già discutibile dal punto di vista del realismo, è anche povera: è povera di implicazioni e produce scarsi risultati in termini di ipotesi falsificabili e di proposizioni determinate.

Infine una riflessione è stata avviata e dovrà essere approfondita sulla 'visione' del mercato che la teoria dell'equilibrio economico generale ci trasmette. Walras scelse il mercato d'asta come tipo reale da cui astrarre il tipo ideale della concorrenza perfetta. Questa scelta è stata densa di implicazioni: ha abituato l'economista teorico a pensare il mercato tout court come un mercato d'asta e, peraltro, come un mercato d'asta improprio e fittizio, perché perfetto dal punto di vista dell'informazione e collocato in un tempo algoritmico astratto che non è quello delle decisioni reali prese sul mercato; ha abituato altresì l'economista teorico a pensare il meccanismo di mercato come riducibile a un meccanismo dei prezzi elementare e trasparente. Nei mercati reali, fuori dalle finzioni della teoria walrasiana, l'armonizzazione e la compatibilità dei fini individuali sul mercato sono raggiunte anche grazie all'operare del meccanismo dei prezzi, ma entro un sistema di istituzioni, di regole, di relazioni di fiducia, di forme e attività organizzative, che non assomiglia affatto al banditore walrasiano.

Il 'libero mercato' è un insieme di istituzioni in cui funzionano meccanismi allocativi e distributivi complessi, assai più ricchi e articolati, indipendentemente dalla loro maggiore o minore efficacia, di quelli descritti dalla teoria dell'equilibrio economico generale.

Ciò che la teoria dell'equilibrio generale ha eliminato dall'analisi della forma ideale del mercato di concorrenza, in quanto 'accidente' irrilevante o in quanto ostacolo al paradigma della razionalità, è proprio ciò che consente di dare un contenuto positivo di conoscenza alla ricerca economica. Gli 'attriti', le specificità storiche e istituzionali dei mercati, le innovazioni tecnologiche, la storia monetaria o industriale, i processi di mutamento sono il materiale indispensabile che fornisce contenuto e determinatezza alla disciplina e le dà una ragione d'essere a fianco di altre forme di riflessione sulle regole della vita associata. (V. anche Concorrenza; Economia; Interdipendenze strutturali, analisi delle; Prezzi).

Bibliografia

Arrow, K. J., The firm in general equilibrium theory, in The corporate economy: growth, competition and innovative potential (a cura di R. Marris e A. Woods), Cambridge, Mass., 1971, pp. 68-110.

Arrow, K. J., Hahn, F.H., General competitive analysis, San Francisco 1971.

Canard, N. F., Principes d'économie politique, Paris 1801.

Chamberlin, E. H., The theory of monopolistic competition, Cambridge, Mass., 1933 (tr. it.: Teoria della concorrenza monopolistica, Firenze 1961).

Cournot, A.-A., Recherches sur les principes mathématiques de la théorie des richesses, Paris 1838 (tr. it.: Ricerche sui principî matematici della teoria delle ricchezze, in Opere, Torino 1981, pp. 125-258).

Cournot, A.-A., Principes de la théorie des richesses, Paris 1863.

Debreu, G., Theory of value: an axiomatic analysis of economic equilibrium, New Haven, Conn., 1959.

Grandmont, J. M. (a cura di), Temporary equilibrium: selected readings, San Diego, Cal., 1988.

Hildenbrand, V., Core and equilibria of a large economy, Princeton, N. J., 1973.

Ingrao, B., Israel, G., La mano invisibile: l'equilibrio economico nella storia della scienza, Roma-Bari 1987.

Israel, G., El declive de la 'mathématique sociale' y los inicios de la economía matemática en el contexto de los avatares del Institut de France, in "Llull. Revista de la Sociedad Española de Historia de las Ciencias y de las Técnicas", 1991, XIV, 26, pp. 59-116.

Jaffé, W. (a cura di), Correspondence of Léon Walras and related papers, 3 voll, Amsterdam 1965.

Jevons, W. S., Theory of political economy, London 1871 (tr. it.: Teoria dell'economia politica e altri scritti economici, Torino 1947).

Negishi, T., Monopolistic competition and general equilibrium, in "Review of economic studies", 1961, XXVIII, pp. 119-126.

Neumann, J. von, Morgenstern, O., Theory of games and economic behavior, Princeton, N. J., 1944.

Pareto, V., Cours d'économie politique, 2 voll., Lausanne 1896-1897 (tr. it.: Corso di economia politica, Torino 1943).

Pareto, V., Manuale di economia politica, Torino 1906.

Roberts, J., Sonnenschein, H., On the foundations of the theory of monopolistic competition, in "Econometrica", 1977, XLV, pp. 101-113.

Scarf, H., The computation of economic equilibria, New Haven, Conn., 1973.

Shubik, M., The many approaches to the study of monopolistic competition, in "European economic review", 1985, XXVI, pp. 97-114.

Smale, S., The mathematics of time. Essays on dynamical systems, economic processes, and related topics, New York 1980.

Walras, L., Éléments d'économie politique pure ou théorie de la richesse sociale, 2 voll., Lausanne 1874-1877; ed. definitiva, Paris 1926 (tr. it.: Elementi di economia politica pura, Torino 1974).

Walras, L., Économique et mécanique, in "Bulletin de la Société Vaudoise des Sciences Naturelles", 1909, XLV.

Weintraub, E. R., General equilibrium analysis: studies in appraisal, Cambridge 1986.