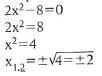equazioni
equazioni
La traduzione matematica di un problema
Le equazioni sono lo strumento per affrontare quasi tutti i problemi che richiedono una risposta quantitativa. Spesso il modo più efficace per risolvere un problema è scrivere un'uguaglianza fra espressioni che mettono in relazione gli elementi noti e quelli sconosciuti del problema. Un'uguaglianza del genere è un'equazione e risolverla equivale a trovare la soluzione del problema. Si incontrano equazioni in moltissime discipline, come la fisica, l'economia, l'informatica. In particolare, la fisica traduce in equazioni, cioè in linguaggio matematico, le sue teorie
Una storia antica
La storia delle equazioni è molto antica. Già gli Egizi e i Babilonesi sapevano risolvere le equazioni più semplici, quelle di primo e di secondo grado, pur non disponendo del simbolismo dell'algebra moderna. Tra il 6° e il 4° secolo a.C. i Greci utilizzavano le equazioni di secondo grado per risolvere problemi geometrici. Nella seconda metà del 3° secolo d.C., il matematico greco Diofanto di Alessandria espose una serie di problemi risolubili mediante equazioni di primo e di secondo grado. Tra la fine dell'8° e l'inizio del 9° secolo il matematico arabo Muhammad ibn Musa al-Khuwaritzmi descrisse in modo sistematico alcuni metodi per risolvere le equazioni, soprattutto di secondo grado.
Nel 16° secolo si occuparono di equazioni specialmente matematici italiani e tedeschi. Fu allora che vennero introdotti i simboli per indicare le espressioni algebriche e scrivere così le equazioni. Ormai le equazioni di secondo grado erano completamente note e ci si dedicò a equazioni di grado superiore.
Le equazioni sono strumenti per risolvere problemi
Un'equazione è un'uguaglianza fra due espressioni, in cui compaiono una o più quantità, dette incognite; essa risulta verificata soltanto per particolari valori assunti dalle incognite. Questa è una definizione strettamente matematica e non rende l'idea dell'importanza delle equazioni. Per accorgersene, conviene considerare la matematica come un linguaggio, un linguaggio molto speciale, che consente di esprimere in modo chiaro e preciso le relazioni fra le grandezze.
Ebbene, un'equazione non è altro che la traduzione, nel linguaggio della matematica, di un problema, che può essere tecnico, scientifico, economico e così via. Più precisamente, un'equazione è una 'frase', scritta nel linguaggio della matematica, che afferma l'uguaglianza di due espressioni in cui compaiono quantità sia costanti sia variabili: i dati e le incognite di un particolare problema. Quasi tutti i problemi che riguardano grandezze, cioè che richiedono una risposta quantitativa, si possono risolvere con le equazioni.
Tradurre i problemi in equazioni
Per risolvere un problema, bisogna impostare l'equazione relativa, cioè scriverla correttamente, traducendo in termini matematici i dati del problema. Ciò vale sia per i semplici problemi che si sottopongono agli studenti che imparano la matematica, sia per i quesiti molto più complessi che gli scienziati debbono affrontare.
Esistono regole precise per risolvere le equazioni, mentre non esistono regole per effettuare la traduzione di un problema ‒ espresso in linguaggio naturale ‒ in equazioni; perciò è molto importante saper analizzare il problema per tradurne correttamente i termini. In particolare è importante: individuare le incognite; individuare le relazioni fra le incognite e i dati noti del problema; scrivere correttamente l'uguaglianza in cui consiste l'equazione.
Per esempio, viene assegnato il seguente problema: "Il quadruplo di un numero è uguale al doppio del numero stesso aumentato di 6. Trovare il numero". Come possiamo procedere? L'incognita è il numero da trovare e lo indichiamo con la lettera x (ma qualunque altra lettera dell'alfabeto andrebbe bene). Il testo del problema dice che il quadruplo del numero da trovare (4x) dev'essere uguale al doppio del numero stesso aumentato di 6, cioè a 2x+6. Il problema si traduce quindi nell'equazione:
4x=2x+6
che si risolve facilmente:
4x−2x=6
2x=6
x=3
Le equazioni di primo grado
Le equazioni più semplici sono quelle di primo grado che si possono scrivere in generale come ax=b, dove la x indica l'incognita, mentre a e b sono numeri qualsiasi.
Sono equazioni di primo grado, per esempio, l'equazione del moto rettilineo uniforme e la prima legge di Ohm. La prima fornisce la proporzionalità fra lo spazio percorso (s) e il tempo (t) impiegato a percorrerlo da parte di un corpo che si muove a velocità (v) costante (s=vt), mentre la seconda esprime la relazione fra la differenza di potenziale ΔV, applicata a un conduttore elettrico di resistenza R, e l'intensità di corrente i che percorre il conduttore (ΔV=iR).
In generale, un'equazione di primo grado ha una soluzione, e una soltanto. Esistono due eccezioni: le equazioni impossibili che non hanno alcuna soluzione e le equazioni indeterminate che hanno invece infinite soluzioni.
L'equazione x+1=x−2 è impossibile, perché non esiste un numero tale che, aggiungendogli 1 e sottraendogli 2, dia uno stesso numero; l'equazione
3(x+2)=6x/2+18/3
è indeterminata, perché è soddisfatta da qualsiasi numero.
Le due equazioni che seguono
3x=6
(x−1)/4 +x/2=5/4
hanno la stessa soluzione (x=2), come si può verificare subito, sostituendo, al posto della x, il numero 2; si dicono, perciò, equivalenti:
3 . 2=6
(2−1)/4+2 /2=1/4−2/2=1/4+4/4=5/4
Date due equazioni equivalenti, per trovarne la soluzione, si può risolvere l'una o l'altra. Ovviamente conviene risolvere quella… più semplice.
Applicando i principi e le regole di trasformazione, si possono risolvere meccanicamente tutte le equazioni di primo grado a un'incognita. Non altrettanto 'automatico', come già accennato, è il compito di impostare l'equazione che traduce in termini matematici un determinato problema.
I sistemi di primo grado
Supponiamo di dover risolvere il seguente problema: "Trovare due numeri tali che la loro differenza sia uguale a 1 e la loro somma uguale a 7". Un semplice ragionamento permette di tradurre il quesito in un'equazione di primo grado a un'incognita. Infatti, se la differenza fra i due numeri è 1, si può chiamare x il numero più grande e x−1 il numero più piccolo e scrivere (ricordando che la somma dei due numeri vale 7):
x+(x−1)=7
2x−1=7
2x=7+1=8
x=4
x−1=3
Ma si può anche risparmiare il semplice ragionamento e tradurre direttamente il problema in due equazioni a due incognite (x e y), due 'frasi' che esprimono, ciascuna, una condizione del problema:
x +y=7
x−y=1
L'insieme delle due equazioni scritte è un sistema di equazioni di primo grado in due incognite. Risolvere un sistema di questo tipo significa trovare un valore per la x e un valore per la y capaci di soddisfare tutte e due le equazioni. Esistono diversi metodi per risolvere un sistema di primo grado. Nel caso del nostro sistema, si può, per esempio, scrivere la x in funzione della y nella seconda equazione
x+y=7
x=y+1
e poi sostituire nella prima equazione y+1 al posto della x:
y+1+y=7
x=y+1
La prima equazione è così diventata un'equazione a una sola incognita e si può risolvere come sappiamo. Una volta ottenuto il valore della y (nel nostro caso 3), lo si sostituisce nella seconda equazione e si ricava anche quello della x. Questo sistema si chiama metodo di sostituzione.
Analogamente a quanto accade nel caso delle equazioni di primo grado, anche nel caso dei sistemi di primo grado, generalmente, esiste un'unica soluzione (data da una coppia di valori). Fanno eccezione i sistemi impossibili (nessuna soluzione) e i sistemi indeterminati (infinite soluzioni).
Le equazioni di secondo grado
Un'equazione si dice di secondo grado quando l'incognita vi compare (anche) con esponente 2. Le equazioni di secondo grado si presentano in tre forme:
(1) ax2+bx+c=0
(2) ax2+c=0
(3) ax2 +bx=0
La (1) si chiama equazione di secondo grado completa; la (2) equazione pura; la (3) equazione spuria. Tutte le equazioni di secondo grado possiedono due soluzioni (in generale, le soluzioni di un'equazione algebrica sono in numero pari al grado dell'equazione). L'equazione 'pura' 2x2−8=0 si risolve come segue:
Infatti sono due i numeri che elevati alla seconda danno 4: +2 e −2.
L'equazione 'spuria' 6x2−18x=0 si risolve prendendo a fattor comune la x al primo membro:
x(6x−18)=0
Quindi, ricordando che un prodotto di due fattori si annulla quando uno dei due fattori è uguale a 0, si ottengono le due soluzioni uguagliando a 0 i due fattori a primo membro:
x1=0
6x−18=0
6x=18
x2=3
Come si può verificare facilmente, le due soluzioni della nostra equazione sono 0 e 3.
Per risolvere l'equazione completa di secondo grado, bisogna applicare la formula risolutiva:
Data l'equazione completa x2−5x+6=0, le sue due soluzioni sono:
Equazioni algebriche di grado superiore al secondo ed equazioni non algebriche
Un'equazione algebrica, ossia un polinomio (algebra) uguagliato a zero, si dice risolubile per radicali se le sue soluzioni sono ottenibili con un numero finito di operazioni razionali (addizioni, sottrazioni, moltiplicazioni, divisioni) ed estrazioni di radice. Per esempio, le equazioni di secondo grado sono risolubili per radicali.
Soltanto intorno alla metà del Cinquecento, per merito dei matematici italiani Scipione Dal Ferro, Niccolò Fontana (detto Tartaglia) e Gerolamo Cardano, fu trovata la formula risolutiva dell'equazione di terzo grado. A Ludovico Ferrari, altro matematico italiano, si deve la formula risolutiva dell'equazione di quarto grado.
I matematici, visti questi risultati, speravano di poter trovare anche le formule risolutive delle equazioni di grado superiore, a cominciare da quelle di quinto grado. Ma speravano invano. Dopo un lunghissimo periodo di inutili tentativi per trovare la formula risolutiva delle equazioni di quinto grado, l'italiano Paolo Ruffini e il norvegese Niels Henrik Abel dimostrarono che, in generale, un'equazione di grado superiore al quarto non è risolubile per radicali.
Oltre alle equazioni algebriche, di cui ci siamo occupati, esistono molti altri tipi di equazioni: le equazioni trigonometriche, le equazioni logaritmiche, le equazioni diofantee, le equazioni differenziali, le equazioni integrali e via dicendo. In questi casi, le incognite possono essere non solo numeri, ma anche funzioni; tuttavia il concetto di equazione resta lo stesso: si tratta sempre di un'uguaglianza fra espressioni che contengono incognite.
Le equazioni sono il 'regalo' più utile che la matematica abbia fatto a tutte quelle discipline che si occupano della conoscenza di qualche aspetto del mondo reale, in quanto strumenti adattabili alla soluzione dei problemi più vari.
Come impostare un'equazione
Vediamo come impostare sotto forma di equazione il seguente problema.
"Una certa quantità di vino può essere contenuta esattamente in 4 recipienti uguali, grandi, o in 6 recipienti uguali più piccoli. Ogni recipiente piccolo contiene 10 litri meno di un recipiente grande. Trovare la quantità di vino".
Chiamiamo x i litri di vino contenuti in un recipiente grande; allora i quattro recipienti grandi conterranno 4x litri di vino. Dai dati del problema, sappiamo che ogni recipiente piccolo contiene x−10 litri di vino; perciò i recipienti piccoli contengono, tutti insieme, 6(x−10) litri di vino. Le due quantità 4x e 6(x−10) devono essere uguali. L'equazione che traduce il problema è dunque 4x=6(x−10) e si risolve facilmente:
4x=6x−60
6x−4 x=60
2x=60
x=30
Ricordando che abbiamo chiamato x la quantità di vino contenuta in un recipiente grande, avremo che la quantità totale di vino è 4x, cioè 120 litri (ogni recipiente grande contiene 30 litri di vino, ogni recipiente piccolo ne contiene 20).