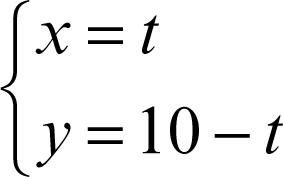equazione

equazione

equazione uguaglianza tra due espressioni contenenti una o più variabili, dette incognite dell’equazione. Per esempio, le equazioni x + 1 = 3 e x ² − 5x + 6 = 0 hanno una incognita, mentre x + y = 10 ha due incognite. Le due espressioni a sinistra e a destra del segno di uguaglianza sono dette, rispettivamente, primo e secondo membro dell’equazione. Assieme a un’equazione viene assegnato un dominio, vale a dire un insieme di valori delle incognite per cui l’equazione ha significato e che specifica la natura delle incognite stesse. Una soluzione di un’equazione è una qualsiasi determinazione delle incognite, all’interno del dominio assegnato, che renda soddisfatta l’uguaglianza, ossia renda il primo membro uguale al secondo. Risolvere un’equazione significa determinarne l’insieme delle soluzioni, vale a dire l’insieme dei valori che appartengono al suo dominio e soddisfano l’uguaglianza. Per esempio {2, 3} è l’insieme delle soluzioni dell’equazione x ² − 5x + 6 = 0, di dominio R, perché è vero sia 2² – 5 · 2 + 6 = 0 sia 3² – 5 · 3 + 6 = 0 e si può dimostrare che non c’è alcun altro valore reale che soddisfa l’uguaglianza. A seconda del tipo, della complessità o del contesto numerico in cui si cerca la soluzione, un’equazione può avere nessuna soluzione, un numero finito di soluzioni, oppure infinite soluzioni.

Un’equazione soddisfatta da qualunque determinazione delle incognite nel dominio assegnato è detta identità (o anche equazione identica); se invece essa non è soddisfatta per nessuna determinazione delle incognite all’interno del dominio, allora l’equazione è detta equazione impossibile o contraddizione. Un’equazione che sia identica o impossibile è detta impropria: questo è per esempio il caso dell’equazione x = x, che è un’identità, o dell’equazione x + 1 = x + 2, che è un’equazione impossibile, dove il dominio è un qualsiasi insieme numerico. Un’equazione che non sia impropria è detta propria. La risolubilità di un’equazione è strettamente legata al dominio in cui la si considera: per esempio, l’equazione x ² − 2 = 0 non ha soluzioni nell’insieme Q dei numeri razionali e dunque è impossibile in questo dominio; se come dominio si considera invece l’insieme R dei numeri reali, allora l’equazione è propria e ha come insieme delle soluzioni l’insieme {−√(2), √(2)}. Analogamente, l’equazione x ² + 1 = 0 non ha soluzioni nel campo reale mentre ha soluzioni i e −i nel campo complesso.

Per semplificare un’equazione, si utilizzano dei principi di equivalenza, che permettono di manipolare un’equazione riconducendosi allo studio di un’equazione equivalente, che ammette cioè le stesse soluzioni, ma che risulta più semplice (→ equivalenza, principi di (per equazioni)). La risoluzione di un’equazione può tuttavia risultare difficile o impossibile utilizzando soltanto metodi algebrici. Esistono perciò vari metodi numerici per il calcolo approssimato delle soluzioni di un’equazione: generalmente si ricorre a procedimenti iterativi consistenti nella costruzione di successioni numeriche convergenti a esse, come per esempio nei casi del metodo di → Newton, del metodo delle → secanti e del metodo di → bisezione.

Equazioni in più incognite

Una equazione in n incognite (con n > 1), se propria, ha come soluzioni delle n-ple ordinate di elementi del dominio. Per esempio, per l’equazione x₁ + x₂ + x₃ = 0, di dominio R³, la terna (5, 3, −8) è una tra le sue infinite soluzioni. Una equazione con infinite soluzioni è detta indeterminata. In tali casi l’insieme delle soluzioni può essere descritto attraverso l’uso di opportuni parametri. Per esempio, l’equazione x + y = 10, di dominio R², ha come soluzioni tutte le coppie del tipo (t, 10 − t), al variare di t ∈ R. L’insieme delle sue soluzioni può allora essere descritto in forma parametrica al variare del parametro reale t come l’insieme delle soluzioni del sistema

con t ∈ R. L’insieme delle soluzioni di una equazione in due incognite di dominio R² è generalmente un insieme di infinite coppie ordinate di numeri reali (x, y) che, interpretate come coordinate di punti in un piano cartesiano, descrivono una curva: si parla allora talvolta di equazione della curva (per esempio: equazione di una retta, equazione di una conica ecc.). Analogamente, l’insieme delle soluzioni di una equazione in tre incognite di dominio R³ è generalmente un insieme infinito di terne ordinate di numeri reali (x, y, z) che, in un sistema di riferimento tridimensionale Oxyz, descrivono una superficie. Similmente si può affrontare il caso con un numero superiore di incognite oppure il caso in cui le equazioni siano definite in domini razionali o complessi.

Equazioni algebriche, trascendenti, funzionali

Le equazioni aventi come dominio un insieme numerico si dividono in:

• algebriche: sono le equazioni che, eventualmente dopo opportune trasformazioni, si riducono a essere della forma p(x₁, ..., x_n) = 0, dove p è un polinomio di una o più variabili, con eventuali altre condizioni che ne restringono il dominio (→ equazione algebrica);

• trascendenti: sono le equazioni in cui una o più incognite sono argomento di funzioni trascendenti, quali per esempio le funzioni goniometriche, logaritmiche o esponenziali (→ equazione trascendente). Se le incognite di un’equazione sono delle funzioni, si parla allora di → equazioni funzionali: se, insieme alle funzioni incognite, l’equazione coinvolge anche le loro derivate (cioè implica non solo operazioni dell’algebra ma anche dell’analisi infinitesimale), si parla più in particolare di → equazione differenziale; se invece le funzioni incognite (o alcune di esse) compaiono sotto il segno d’integrale, si parla allora di → equazione integrale.

Equazioni numeriche e letterali

Un’equazione numerica è un’equazione in cui tutte le lettere che vi compaiono sono incognite e i coefficienti sono tutti numerici. Un’equazione letterale o parametrica è un’equazione in cui compaiono lettere, dette parametri, che non sono incognite: tali lettere rappresentano quindi dei dati dell’equazione e, in questo senso, vanno pensati come costanti. Similmente alle incognite, ogni parametro avrà un suo dominio che viene specificato insieme all’equazione. Discutere un’equazione in cui compaiano dei parametri significa analizzare l’esistenza e il numero delle soluzioni dell’equazione al variare dei parametri nei relativi domini. Per esempio, l’equazione ax = 0, di incognita x e parametro a (ambedue reali), se a ≠ 0 ha come soluzione soltanto x = 0 mentre se a = 0 il suo insieme delle soluzioni è tutto R. Le equazioni letterali permettono di prendere in considerazione modelli di equazioni di tipo generale, e, in alcuni casi, permettono di determinare formule risolutive, come per esempio nei casi delle equazioni generali di primo, secondo, terzo e quarto grado in un’incognita.

Sistema di equazioni

Quando in un problema le incognite sono legate da più vincoli indipendenti, la sua formalizzazione matematica è espressa da più equazioni di cui si cercano le soluzioni comuni. A tale proposito, si veda → sistema di equazioni.

Equazione cartesiana di una curva o di un ente geometrico

Qualora un ente geometrico (una retta, una parabola, una circonferenza ecc.) sia definito in un sistema di riferimento cartesiano, del piano o dello spazio, i suoi punti hanno particolari coordinate ed è possibile che queste si caratterizzino per soddisfare particolari condizioni algebriche. Per esempio, in un sistema di riferimento cartesiano del piano Oxy, la retta bisettrice del primo e terzo quadrante è formata da tutti e soli i punti che hanno uguali le due coordinate: essa è pertanto descritta dall’equazione y = x. Quando perciò, nel piano dotato di un sistema di riferimento Oxy, si indica la curva di equazione ƒ(x, y) = 0, si intende definire quella curva i cui punti sono tutti e soli quelli le cui coordinate sono soluzioni dell’equazione ƒ(x, y) = 0. Come ulteriori esempi si possono considerare l’equazione x ² + y ² = 1, che definisce nel piano la circonferenza di centro l’origine e di raggio unitario, e la disequazione x ² + y ² ≤ 1, che definisce il cerchio delimitato dalla precedente circonferenza. Tali considerazioni si estendono naturalmente allo spazio tridimensionale in cui sia definito un sistema di riferimento Oxyz e, nel quale, una formula algebrica del tipo ƒ(x, y, z) = 0, o in forma esplicita z = ƒ(x, y), descrive, con le sue soluzioni, una superficie. Una curva nello spazio è a sua volta descritta mediante il sistema formato dalle equazioni delle superfici di cui la curva è intersezione.

Equazioni parametriche di una curva o un ente geometrico

Nel piano e nello spazio una curva o una superficie possono essere descritte analiticamente da funzioni dipendenti da uno o più parametri. Si veda la voce → parametro.