equazione

equazione

Uguaglianza fra due espressioni algebriche (funzioni) contenenti una o più quantità variabili (incognite dell’e.), verificata solo per alcuni valori di queste (soluzioni o radici dell’e.). Se l’e. è soddisfatta per qualunque valore delle variabili, si ha un’identità. L’esistenza di una o più soluzioni può dipendere dal campo numerico in cui le soluzioni si ricercano; campi tipici sono i numeri reali (che sono in corrispondenza uno a uno con i punti di una retta) o i numeri complessi (esprimibili nella forma a+bi con a e b reali e i =(−1)^1/2, l’unità immaginaria il cui quadrato è −1). Un sistema di e. è un insieme di due o più equazioni. Una soluzione di un sistema è un insieme di valori delle incognite che soddisfano tutte le e. del sistema.

Equazioni algebriche

Sono e. ottenute eguagliando a zero un polinomio (in una o più variabili) il cui grado determina il grado dell’equazione. Il caso più semplice è quello dell’e. algebrica in una sola incognita x. Nel campo complesso ogni e. algebrica di grado n in una variabile ammette esattamente n radici, non necessariamente distinte (teorema fondamentale dell’algebra). La ricerca delle radici per e. algebriche di grado primo e secondo è questione relativamente elementare. Infatti, nel primo caso, ax+b=0 ha soluzione unica

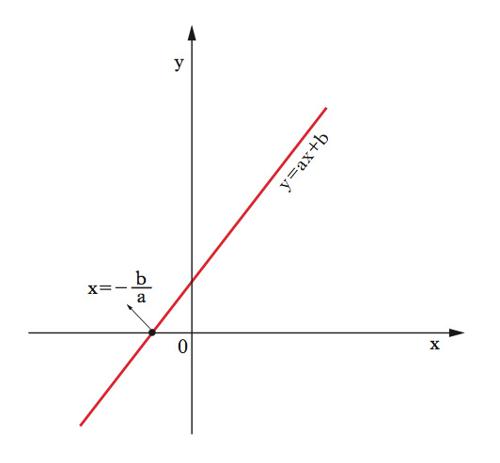
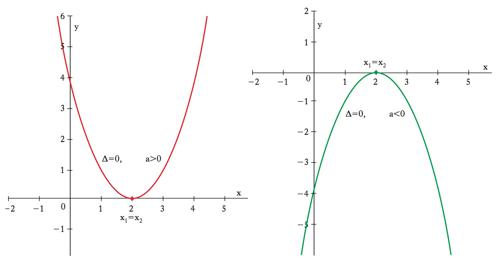
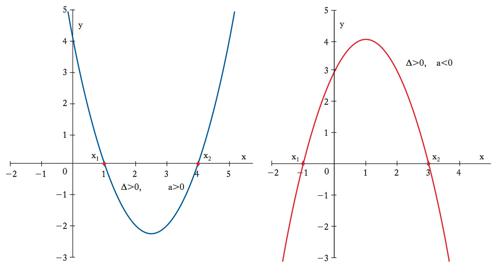
ha due soluzioni: x₁=(−b+Δ^1/2)/2a e x₂=(−b−Δ^1/2)/2a, dove Δ=b²−4ac è detto anche discriminante dell’e. di secondo grado. Le soluzioni sono coincidenti se Δ=0, distinte e reali se Δ>0, distinte e complesse se Δ<0. In un’interpretazione geometrica, dato un sistema di assi coordinati con x sull’asse orizzontale e y su quello verticale, y=ax+b è l’e. di una retta con inclinazione a e la soluzione della ax+b=0 individua il punto (grafico 1) in cui tale retta interseca l’asse orizzontale (di equazione y=0). La y=ax²+bx+c è l’e. di una parabola con asse di simmetria parallelo all’asse verticale, rami rivolti verso l’alto (il basso) se a>0(<0) e coordinate del vertice x_v=(−b/2a),y_v=(−Δ/4a). Se il discriminante è nullo, la parabola è tangente all’asse orizzontale in corrispondenza al vertice (grafico 2) la cui ascissa è allora l’unico punto in cui la parabola tocca l’asse orizzontale (l’unica soluzione dell’e. ax²+bx+c=0). Δ=0; soluzioni coincidenti x₁=x₂. Se il discriminante è positivo, l’ordinata y_v del vertice ha segno opposto a quello di a e quindi vi sono due punti (simmetrici rispetto all’ascissa del vertice) in cui la parabola attraversa l’asse orizzontale (grafico 3). Le ascisse di tali punti sono le due soluzioni reali distinte dell’e. ax²+bx+c=0. Se il discriminante è negativo, l’ordinata del vertice ha lo stesso segno di a e quindi la parabola sta tutta sopra (se a>0) o tutta sotto (se a<0) l’asse orizzontale (grafico 4) e non vi sono punti comuni fra la parabola e l’asse orizzontale (non vi sono soluzioni reali dell’e. ax²+bx+c=0). Si possono in ogni caso determinare mediante operazioni razionali o irrazionali le radici di e. fino al quarto grado (teorema di Ruffini-Abel). La ricerca delle radici corrisponde alla ricerca degli zeri di una funzione polinomiale e si rivela particolarmente preziosa nella ricerca dei punti di ottimo (necessariamente zeri della derivata prima). Altro caso di estremo interesse applicativo in campo economico-aziendale è quello dei sistemi lineari, cioè di m e. algebriche lineari (dove compaiono polinomi di primo grado) in n incognite. Un tale sistema si dice compatibile se esiste almeno una soluzione, determinato se essa è unica. Con riferimento a soluzioni nel campo reale o complesso, condizione necessaria e sufficiente per la compatibilità è che la matrice dei coefficienti e quella estesa ai termini noti abbiano uguale caratteristica p, dimensione massima delle sottomatrici quadrate con determinante non nullo estraibili da una matrice. L’unicità si ha nel caso p=n (teorema di Rouché-Capelli). Se p<n si hanno n−p gradi di libertà, perché fissate p variabili la cui matrice dei coefficienti abbia caratteristica p, si possono scegliere arbitrariamente i valori da attribuire alle altre n−p variabili, rimanendo poi, in corrispondenza a tale scelta, unica la soluzione per le prime p variabili.

Equazioni differenziali

Legame fra una funzione incognita (di una o più variabili) e una o più delle sue derivate. Se nella funzione incognita compare una sola variabile indipendente, si ha un’e. differenziale ordinaria, se due o più, un’e. differenziale alle derivate parziali (EDP). Per es., per funzioni y(x) di una variabile x abbiamo G(x, y(x), y′(x),…,y″(x))=0.

E. differenziali ordinarie del primo ordine EDO1 (di ordine n, EDOn) sono quelle in cui compare al massimo la derivata prima (n-esima). La forma canonica di EDO1 è y′=f(y(x), x) in cui y' è funzione esplicita della funzione y e della variabile x. I seguenti tipi speciali di EDO1 sono di particolare rilievo nelle applicazioni economiche. EDO1 a variabili separabili y′=Φ(y)Ψ(x). Utilizzando la notazione differenziale y′=dy/dx e supposto Φ(y)≠0, si ha dy/Φ(y)=Ψ(x)dx, che consente di integrare separatamente i due membri. EDO1 lineare y′=ya(x)+b(x), che in particolare è detta omogenea se b(x)=0 per ogni x la cui soluzione è y=c∙exp(ʃa(x)dx), con c costante arbitraria. EDO1 di Bernoulli: y′=ya(x)+b(x)y^a con a ≠0 e ≠1. EDO1 di Riccati: y′=ya(x)+b(x)y²+c(x). Una soluzione di un’e. differenziale ordinaria è una funzione y(x) tale che esista un intervallo aperto di valori della x in cui l’e. è identicamente (per ogni x) soddisfatta. La nozione si estende considerando intervalli aperti di Rⁿ alle soluzioni di EDP o di sistemi di EDP. Una EDO in forma canonica di ordine n si può sempre ricondurre a un sistema di n EDO1 in forma canonica. Si può dimostrare che l’integrale generale, ovvero l’insieme di tutte le soluzioni di una EDO di ordine n, coinvolge n costanti arbitrarie. Assegnati particolari valori al vettore c che le raccoglie, si ottiene un integrale particolare. Sovente il problema che interessa è proprio quello di estrarre dall’integrale generale quell’integrale particolare in cui le costanti sono gli specifici valori (dette anche condizioni iniziali) assunti in un certo valore x₀ dalle y, y′,…,y⁽ⁿ⁾. Questo problema è noto come problema di Cauchy (➔ Cauchy, metodo di). I teoremi di Picard-Lindelöf e Peano-Cauchy garantiscono, sotto opportune condizioni, esistenza e unicità di soluzioni locali (in un intorno di x₀) e la loro prolungabilità al problema di Cauchy per EDO (sistemi di EDO) in forma canonica. Un esempio di EDO1 lineare omogenea di grande rilievo in finanza quantitativa è la M′(t)=r(t)M(t) in cui r è una funzione nota del tempo t e l’incognita M(t) è il valore all’epoca t del conto corrente non rischioso. Posto M(0)=K, la soluzione del corrispondente problema di Cauchy è M(t)=Kexp[ʃ₀^tr(u)du], corrispondente nella versione discreta alla M(n)=K(1+i)ⁿ. Altro esempio di EDO1 lineare non omogenea rilevante è la r′(t)=ac−ar(t) (con (a,c) una coppia di costanti positive) che descrive l’evoluzione nel tempo del tasso istantaneo di interesse a pronti (spesso utilizzata nella versione dr=a(c−r)dt, in cui a primo membro compare il differenziale del tasso istantaneo). Con la condizione r(0)=r₀, la soluzione del problema di Cauchy è r(t)=r_oexp(−at)+c(1−exp(−at)).

Equazioni differenziali stocastiche

Equazioni (EDS) in cui l’incognita è una funzione aleatoria, in linguaggio probabilistico un processo stocastico X(t). Una tipica EDS nella funzione aleatoria X(t) si presenta nella forma dX_t=μ(X_t,t)dt+σ(X_t,t)dB_t, dove dB è il differenziale di un un processo di Wiener (moto browniano standard, ➔ browniano, moto). Essa va intesa come un modo alternativo di esprimere la seguente e. integrale

X_t+s−X_t=∫_t^t+sμ(X_u,u)du+∫_t^t+sσ(X_u,u)dB_u

che descrive l’incremento nel tempo del processo aleatorio continuo X_t come somma di due componenti. Il significato intuitivo è che nell’intervallo di tempo dt il differenziale stocastico dX è una variabile aleatoria di media μ(X_t,t) dt e varianza σ(X_t, t)²dt.