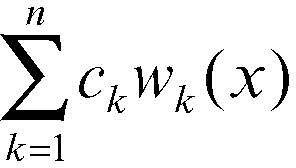equazione differenziale
equazione differenziale
equazione differenziale equazione che stabilisce un legame tra una o più funzioni incognite e una o più delle loro derivate (parziali se le variabili indipendenti sono più di una). Un’equazione differenziale si dice ordinaria quando compaiono in essa solo funzioni di una sola variabile. Un’equazione differenziale ordinaria è di ordine n se la sua incognita è una funzione di una variabile che compare in essa assieme alle sue derivate fino a un certo ordine n. Essa ha la forma generale
in cui deve sussistere effettivamente la dipendenza dalla derivata n-esima, mentre l’incognita y oppure le sue derivate intermedie potrebbero non essere presenti.
Un’equazione differenziale si dice in forma normale se ha la struttura
Una soluzione (o integrale) in senso classico dell’equazione differenziale qui sopra scritta è una funzione y(x), di classe Cn in un intervallo (a, b), che sostituita nella funzione F insieme alle sue derivate la soddisfa, cioè la trasforma in una identità in (a, b). La totalità delle soluzioni di un’equazione differenziale si chiama integrale generale dell’equazione data; nelle ipotesi del teorema di esistenza e unicità delle soluzioni per il problema di → Cauchy, esso è costituito da una famiglia di curve (curve integrali) dipendente da n costanti arbitrarie (→ curva integrale). In particolare, la soluzione generale o integrale generale di una equazione differenziale è una famiglia di soluzioni dipendente con continuità da un numero di parametri pari all’ordine dell’equazione, in modo che sia sempre possibile verificare una assegnata condizione iniziale; una soluzione particolare o integrale particolare è una soluzione ottenuta da una soluzione generale assegnando un particolare valore ai parametri. Si chiama invece soluzione singolare o integrale singolare una soluzione che non sia soluzione particolare, cioè che non sia ottenibile da quella generale mediante un’opportuna assegnazione di valore al parametro.
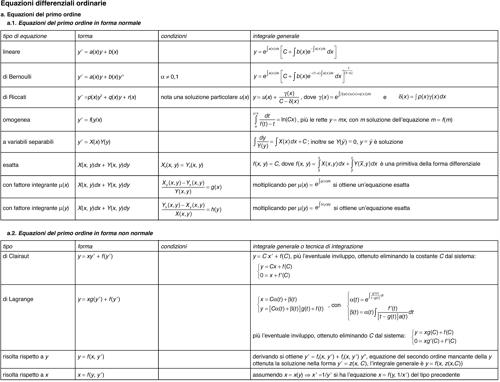
Non esiste una formula risolutiva che descriva l’integrale generale di una equazione differenziale, neppure nel caso più semplice dell’equazione del primo ordine in forma normale, y′ = ƒ(x, y). Solo quando ƒ assume delle forme particolari è possibile portare l’equazione alle quadrature, cioè trovare una formula che ne esprima l’integrale generale mediante gli integrali di funzioni date (→ equazione differenziale, integrale di una; → equazione differenziale lineare, integrale di una; si vedano inoltre le tavole delle equazioni differenziali ordinarie). È possibile, tuttavia, compiere una analisi qualitativa delle soluzioni, descrivendone il grafico anche senza conoscerne l’equazione esplicita, tenendo conto del significato geometrico dell’equazione differenziale. Infatti, una equazione differenziale del primo ordine, y′ = ƒ(x, y), rappresenta un legame tra le coordinate di un punto (x, y) e la pendenza y′ della tangente alla curva integrale passante per tale punto. Quindi, i punti del piano in cui risulta ƒ(x, y) = 0 sono punti stazionari per le soluzioni, mentre laddove risulta ƒ(x, y) > 0 le curve soluzioni sono strettamente crescenti e sono decrescenti dove ƒ(x, y) < 0. Derivando poi l’equazione (cosa lecita se ƒ è sufficientemente regolare) si ottiene il valore della derivata seconda y″ = ƒx(x, y) + ƒy(x, y)y′ = ƒx(x, y) + ƒy(x, y)ƒ(x, y), per cui si possono analogamente trovare i punti in cui le curve integrali hanno derivata seconda positiva, nulla o negativa. Tenendo conto che, per equazioni del primo ordine in forma normale e ƒ sufficientemente regolare, due linee integrali non si possono intersecare (essendo unica la soluzione nell’intorno di un punto), si può tracciare il grafico qualitativo delle soluzioni. La possibilità di calcolare le derivate successive permette comunque lo studio qualitativo locale (cioè nell’intorno di un punto) delle soluzioni, tramite il corrispondente sviluppo di Taylor (→ Taylor, serie di). Il metodo si può estendere a equazioni di ordine superiore o a sistemi di equazioni differenziali (→ sistema differenziale), in particolare al caso autonomo, nel quale non compare esplicitamente la dipendenza dalla variabile indipendente x.
La situazione è più complessa per equazioni in forma non normale, per le quali si rinvia al lemma → Cauchy, problema di. Altri problemi importanti che si possono associare a un’equazione differenziale di ordine n ≥ 2 sono i problemi ai limiti (→ equazioni differenziali, problemi ai limiti per).
Assai importante è il caso delle → equazioni differenziali lineari, nelle quali la funzione F ha la forma di un polinomio di primo grado nell’incognita y e nelle sue derivate. Esse hanno dunque la forma:
Se b(x) = 0 l’equazione è detta omogenea (in caso contrario non omogenea). Per l’equazione omogenea vale il principio (teorema) di sovrapposizione, per cui una combinazione lineare di soluzioni è ancora una soluzione. Se ne deduce che l’integrale generale di un’equazione differenziale lineare omogenea è una combinazione lineare
di n integrali particolari wk(x), purché linearmente indipendenti (si dice che essi costituiscono un sistema fondamentale di soluzioni), che vengono raccolti nella cosiddetta → matrice wronskiana. A partire da questa è possibile anche costruire un integrale particolare p(x) dell’equazione completa, il cui integrale generale è dato dalla somma di p(x) e dell’integrale generale dell’equazione omogenea associata. Il calcolo esplicito di tali soluzioni è possibile solo in casi particolari, come quello delle equazioni a coefficienti costanti e delle equazioni di → Eulero.
lettE_01010.rtf