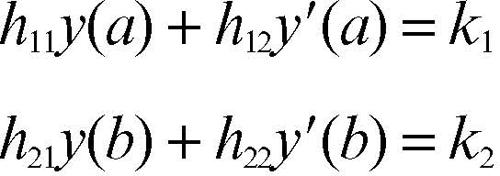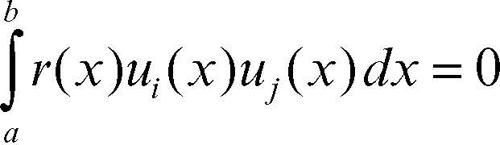equazione differenziale, problemi ai limiti per una

equazione differenziale, problemi ai limiti per una

equazione differenziale, problemi ai limiti per una problemi di grande importanza in quelle applicazioni in cui vengono assegnate delle condizioni agli estremi dell’intervallo all’interno del quale si vuole studiare un’equazione differenziale. In particolare l’equazione differenziale deve soddisfare le condizioni che garantiscano l’esistenza della soluzione in grande, cioè definita a priori su tutto l’intervallo e non solo localmente nell’intorno dei dati iniziali. Si dice perciò che i problemi ai limiti sono problemi in grande, a differenza del problema di → Cauchy, che è a priori un problema in piccolo, nel senso che la sua soluzione è ricercata in un intorno di ampiezza a priori ignota dell’unico punto in cui sono assegnate le condizioni iniziali. Come semplici esempi applicativi, si pensi a una corda o a una trave vincolata ai due estremi, al moto di un punto che deve raggiungere una destinazione in un tempo assegnato, a una parete che conduce calore in condizioni stazionarie. Ancora più rilevanti sono però le applicazioni alle equazioni differenziali alle derivate parziali.

Poiché le condizioni in un problema ai limiti sono almeno due, l’equazione deve essere almeno del secondo ordine. Si tratta qui di seguito questo caso, con l’avvertenza che la generalizzazione non presenta sostanziali variazioni. Si supponga inoltre che il problema ai limiti sia lineare, essendo la trattazione nel caso non lineare assai più complessa. Si consideri dunque un’equazione lineare del secondo ordine, a₀(x)y″ + a1(x)y′ + a2(x)y = b(x), a coefficienti continui in un intervallo chiuso e limitato [a, b], con a0(x) ≠ 0. Sotto queste ipotesi, l’integrale generale dell’equazione è dato da y(x) = C₁w₁(x) + C2w2(x) + p(x), dove w_k(x) sono due integrali linearmente indipendenti dell’omogenea associata e p(x) è un integrale particolare dell’equazione completa. Un problema ai limiti lineare separato nell’intervallo [a, b] è dato dal sistema a due condizioni della forma

nel quale i coefficienti h_ij di ogni riga si intendono non entrambi nulli. Sostituendo l’integrale generale in tali condizioni, si ottiene un sistema lineare nelle due costanti incognite C₁ e C₂, sistema che ammette una e una sola soluzione nel caso in cui il determinante Δ dei coefficienti sia diverso da zero, mentre nel caso Δ = 0 possono esservi nessuna o infinite soluzioni, a seconda che la matrice ampliata sia di rango maggiore o uguale a quella della matrice dei coefficienti (→ Rouché-Capelli, teorema di). In particolare, nel caso omogeneo esistono sempre soluzioni: quella identicamente nulla quando Δ ≠ 0, infinite per Δ = 0.

Il caso veramente interessante nelle applicazioni si ha quando nei coefficienti dell’equazione o del problema è presente un parametro λ. Si ha allora Δ = Δ(λ), per cui la discussione precedente mostra che per i valori di λ per cui Δ(λ) ≠ 0 si ha sempre una e una sola soluzione. I valori di λ che invece risolvono l’equazione Δ(λ) = 0 sono detti autovalori del problema ai limiti e, in corrispondenza a essi, il problema ai limiti omogeneo ammette infinite soluzioni, dette autofunzioni o autosoluzioni, definite a meno di una costante moltiplicativa. Nel caso degli autovalori, il problema ai limiti omogeneo ammette infinite soluzioni anche se il problema completo può non ammettere soluzioni; tuttavia se le ammette, ed è questo il caso in cui vengano soddisfatte opportune condizioni di compatibilità, esse sono infinite e differiscono tra loro per una autosoluzione. Si considerino i seguenti tre esempi:

1) L’equazione y″ + λy = 0 ammette come integrale generale per λ = −α² < 0 le funzioni y = C1e^αx + C2^–αx, per λ = 0 le funzioni y = C1 + C2x e per λ = ω² > 0 le funzioni y = C₁cosωx + C₂sinωx.

Se a essa si associa il problema ai limiti y(0) = 0, y(π) = 0 si ottiene che nei primi due casi risulta necessariamente C₁ = C₂ = 0, mentre nel terzo si ottiene il sistema C₁ = 0, C1cosωπ + C₂sinωπ = 0. Il determinante dei coefficienti è Δ(ω²) = sinωπ, e si annulla per ω = n intero positivo. Pertanto gli autovalori sono λ_n = n2 e le autofunzioni corrispondenti sono y = C₂sinnx, con C₂ arbitraria;

2) Se per la stessa equazione si considera un problema ai limiti non separato, come per esempio il problema y(0) = y(π), y′ (0) = y′ (π), che caratterizza le soluzioni periodiche, si hanno ancora gli autovalori λ_n = n², ma le autofunzioni sono y = C1cosnx + C2sinnx;

3) Considerando il caso y″ +y = 0, y(0) + λy′ (0) = 0, y(π) + y′ (π) = 0 si trova che esiste un solo autovalore, λ = 1, per il quale le autofunzioni sono y = C₁(cosx + − sinx).

Il caso degli infiniti autovalori si verifica ogniqualvolta l’equazione si possa scrivere nella cosiddetta forma autoaggiunta (p(x)y′ )′ + (λr(x) − q(x))y = 0, con p(x) > 0, r(x) > 0 in [a, b]. Ciò si può ottenere dividendo per a0(x) e ponendo

se il parametro λ compare linearmente nel solo termine a2(x). In questo caso si dimostra che il problema ai limiti dato ammette infiniti autovalori λ_n, n ≥ 0, che formano una successione monotòna crescente con λ_n → +∞, per n → ∞. L’autofunzione u_n(x) (unica a meno di una costante) corrispondente a λ_n ammette esattamente n zeri in (a, b). Nell’esempio 1) precedente, è λ_n = n + 1, e infatti u0(x) = sinx, corrispondente a λ₀, non ha zeri in (0, π). Inoltre, autofunzioni corrispondenti ad autovalori distinti sono tra loro ortogonali nel senso dello spazio L2(a, b) con peso r(x), ossia:

per i ≠ j. Questi fatti sono alla base della teoria degli sviluppi di Fourier generalizzati, di capitale importanza nello studio delle equazioni differenziali alle derivate parziali (→ Fourier, serie di).

La teoria si estende poi ai casi singolari, nei quali l’intervallo [a, b] viene sostituito da un intervallo non limitato o da un intervallo aperto (a, b), a uno o a entrambi gli estremi del quale il termine p(x) si annulli. Sotto opportune ipotesi è possibile che la teoria si estenda senza sostanziali differenze (è il caso, per esempio, delle equazioni di → Bessel, e di quelle che danno luogo alle famiglie di polinomi ortogonali), ma in generale accanto o al posto dello spettro puntuale formato dagli autovalori compare uno spettro continuo, formato da un intervallo di valori di λ, e la serie si trasforma in un integrale. È il caso, per esempio, della trasformata di Fourier (→ Fourier, trasformazione di).