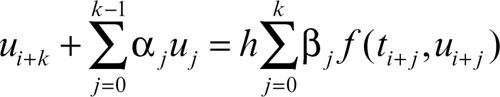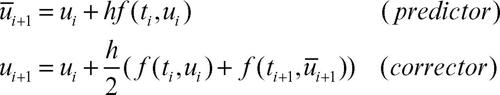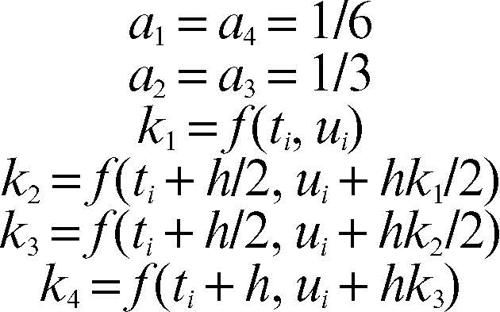equazione differenziale, metodo numerico per la risoluzione di una

equazione differenziale, metodo numerico per la risoluzione di una

equazione differenziale, metodo numerico per la risoluzione di una metodo applicato per la ricerca delle soluzioni approssimate di una equazione differenziale. Supponendo verificate le ipotesi di esistenza e unicità della soluzione dell’equazione differenziale data, esistono vari metodi numerici, che si distinguono tra loro sia per la tipologia di equazione cui si applicano, sia per gli algoritmi di ricerca della soluzione. Per il problema di → Cauchy i metodi più usati fanno ricorso a un procedimento di discretizzazione, consistente nell’approssimare la soluzione su un insieme finito (rete) di punti t₀, t1, …, t_n, presi di solito a uguale distanza h (passo di discretizzazione) e quindi nel costruire una funzione di rete, u, il cui valore in ciascuno dei punti viene assunto come approssimazione del valore della soluzione. La funzione u è scelta in modo da soddisfare una → equazione alle differenze di ordine k del tipo

dove k, α_j e β_j sono costanti caratteristiche del metodo. L’efficacia del metodo è legata all’errore locale di troncamento (la quantità a meno della quale in ogni punto della rete la soluzione soddisfa lo schema approssimato), all’errore globale di discretizzazione (lo scarto, in ogni punto, tra il valore u_i+_k calcolato con lo schema approssimato, e il valore, y(t_i+_k), assunto dalla soluzione) e all’errore di arrotondamento (dovuto all’esecuzione dei calcoli). Un metodo si dice di ordine p se l’errore locale di discretizzazione è proporzionale a h^p+1. Un metodo è detto esplicito se nella (1) è β_k = 0 (cioè è possibile ricavare u_i+k), implicito se β_k ≠ 0. L’uso accoppiato di una formula esplicita e di una formula implicita produce metodi detti metodi predittore-correttore (spesso indicati in inglese come predictor-corrector; → Heun, metodo di), nei quali, a ogni passo, la formula esplicita “predice” il valore di u in un nuovo punto della rete e la formula implicita lo “corregge”. Per esempio,

I metodi fondati sull’uso di formule del tipo (1) sono detti a passo multiplo (multi-step) in quanto, nel caso generale k > 1, per ottenere il valore di u in un punto della rete è necessario disporre di k valori “precedenti” (in particolare, per generare u_k occorrono k “valori di innesco” u0, …, u_k−1). I metodi a passo singolo (single-step) sono invece caratterizzati dal fatto che ognuno dei valori u_i+1 dipende solo dal valore u_i costruito al passo precedente. La classe dei metodi numerici a passo singolo genera a ogni singolo passo di calcolo una soluzione approssimata, in corrispondenza di ciascun incremento finito dell’intervallo d’integrazione; si produce pertanto un insieme discreto di valori della funzione, rappresentante la soluzione approssimata dell’equazione differenziale nell’intervallo considerato; a questa classe appartiene, per esempio, il metodo di → Eulero. Particolare importanza rivestono i metodi di → Runge-Kutta espliciti a r passi (sono, quindi, metodi a passo multiplo), del tipo

dove k1, …, k_r sono valori di ƒ calcolati nell’intorno di t_i. Scelte opportune dei parametri permettono di ottenere formule di ordine assegnato. In particolare, nel metodo di Runge-Kutta “classico” di ordine 4 è

La maggior parte dei metodi numerici per le equazioni differenziali sono stati sviluppati originariamente per risolvere il problema di Cauchy del primo ordine, da cui il nome di metodi numerici del primo ordine; infatti si può dimostrare che è sempre possibile, tramite opportune sostituzioni, trasformare un’equazione differenziale di ordine superiore in un sistema di equazioni differenziali del primo ordine; pertanto questi metodi del primo ordine mantengono una completa generalità, sebbene gli algoritmi implementati diventino sempre più complessi al crescere dell’ordine dell’equazione e meno stabili (→ algoritmo, stabilità di un). Esistono tuttavia metodi numerici diretti di ordine successivo al primo, solitamente del secondo ordine, fondati sullo sviluppo di → Taylor della funzione e troncato sino al termine voluto. Si dimostra inoltre che il resto dello sviluppo di Taylor è alla base della stima dell’errore che si commette nella risoluzione dell’equazione differenziale, determinabile con una precisione che dipende dal grado del troncamento effettuato nello sviluppo. Inoltre, nel caso di equazioni differenziali alle derivate parziali, si utilizzano metodi di approssimazione che si basano sull’approssimazione finito-dimensionale del problema, come il metodo di Faedo-Galërkin (un’applicazione feconda del quale si trova, per esempio, nel metodo degli → elementi finiti), riconducendosi a risolvere equazioni differenziali ordinarie che possono essere trattate con i metodi sopra descritti. Il nome del metodo deriva dal matematico russo B.G. Galërkin, che sviluppò metodi di passaggio dalla risoluzione di un problema definito in uno spazio continuo alla risoluzione del problema stesso in uno spazio discreto per determinarne una soluzione numerica approssimata, e dal matematico italiano A. Faedo che sviluppò un metodo per l’approssimazione delle soluzioni delle equazioni lineari del secondo ordine, di tipo iperbolico e di tipo parabolico.

Per i problemi di valori ai limiti (→ equazione differenziale, problemi ai limiti per una), i metodi di puntamento sono fondati sull’idea di associare al problema assegnato una famiglia di problemi di Cauchy dipendente da un parametro che si cerca di determinare in modo da soddisfare le condizioni date. Nei metodi alle → differenze si sostituiscono alle derivate opportuni rapporti incrementali. Nei metodi di collocazione si ricerca un’approssimazione della soluzione nello spazio delle funzioni polinomiali a tratti di grado m i cui coefficienti vengono determinati richiedendo che, in ogni sottointervallo della rete, il polinomio cui si riduce la funzione soddisfi esattamente l’equazione differenziale in corrispondenza di m punti assegnati e, inoltre, si raccordi con continuità negli estremi con il polinomio “adiacente”. I metodi variazionali si fondano sul fatto che le soluzioni di alcuni importanti tipi di problemi possiedono certe proprietà di minimo per un opportuno funzionale (→ variazioni, calcolo delle). In ognuno dei metodi considerati si perviene alla risoluzione di un sistema algebrico: l’analisi degli algoritmi più idonei alla risoluzione costituisce un capitolo importante dell’analisi numerica.