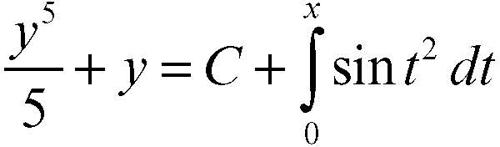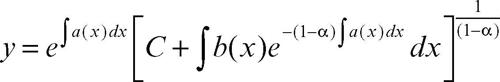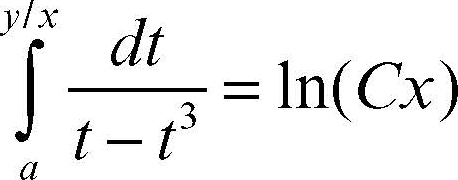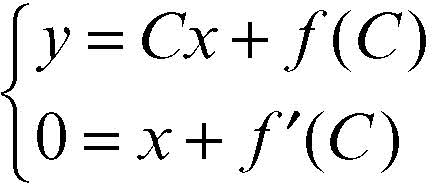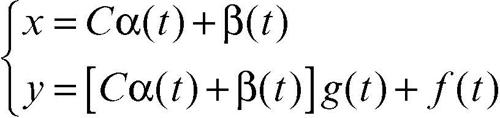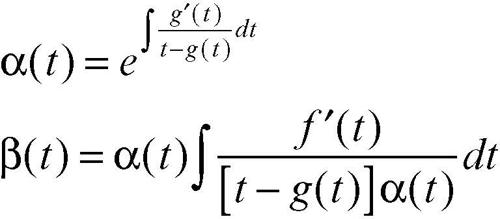equazione differenziale, integrale di una

equazione differenziale, integrale di una

equazione differenziale, integrale di una locuzione che, senza ulteriori specificazioni, indica ‘l’integrale generale di un’→ equazione differenziale, e dunque l’insieme di tutte le soluzioni. La determinazione dell’integrale generale di un’equazione differenziale in forma esplicita non è possibile se non in casi particolari. Un’equazione differenziale si considera completamente risolta analiticamente quando è, come si usa dire, portata alle quadrature, cioè quando si è trovata una formula che ne rappresenta l’integrale generale sotto forma di integrali di funzioni date, con tante costanti arbitrarie quanto è l’ordine dell’equazione. In alcuni casi è possibile indicare un metodo per semplificare l’equazione, ottenendo soluzioni parziali o trasformandola in un’equazione che si sappia risolvere.

I casi più importanti in cui si riesce a portare alle quadrature un’equazione differenziale sono indicati nel seguito.

Equazione differenziale del primo ordine in forma normale

Per un’equazione differenziale del primo ordine in forma normale, y′ = ƒ(x, y), sono riconducibili alle quadrature i seguenti tipi:

• Equazione differenziale a variabili separabili. Si ha quando ƒ(x, y) ha la forma di un prodotto di funzioni dipendenti ciascuna da una sola variabile, cioè quando ƒ(x, y) = X(x) · Y(y). Se esistono radici

dell’equazione Y(y) = 0, le funzioni costanti

sono soluzioni dell’equazione differenziale. Per

è possibile dividere per Y(y), e si può così riscrivere l’equazione nella forma dy /Y(y) = X(x)dx (da cui il nome). Integrando si ha allora

cioè l’integrale generale nella forma implicita G(y) = F(x) + C.

La primitiva G a primo membro, in ogni intervallo in cui Y è diversa da zero, è monotòna in y; è quindi possibile invertirla, ottenendo y = G⁻¹(F(x) + C)). Si noti che sia la determinazione di G che la sua inversione sono concettualmente possibili, anche se nella pratica possono non essere eseguite con metodi elementari. Per esempio, l’equazione differenziale y′ = y ²sinx ammette l’integrale particolare y = 0. Per y ≠ 0, si ha dy /y 2 = sinxdx, da cui, integrando, si ottiene −1/y = −cosx + C e infine y = 1/(cosx – C). Analogamente l’equazione differenziale

dà

In questo caso la funzione a primo membro non può essere invertita elementarmente, pur essendo invertibile in quanto strettamente monotòna, mentre l’integrale a secondo membro non è elementare e dunque la soluzione non è esplicita o come si dice non esprimibile in forma chiusa.

• Equazione lineare. Ha la forma y′ = a(x)y + b(x); l’integrale generale è dato dalla formula

Per esempio, si consideri l’equazione differenziale: y′ = y /x + x ². Si ha:

da cui

(La costante K = ±C ingloba il segno di x, permettendo di eliminare il modulo). Si badi tuttavia che, in senso classico, gli integrali devono essere considerati solo in una delle semirette (−∞, 0) o (0, +∞), in quanto la retta x = 0 è esclusa dal dominio di ƒ(x, y) e pertanto l’equazione differenziale non è ivi definita. D’altra parte, si può studiare il limite per x → 0 della soluzione, osservando che per x = 0 le soluzioni sono prolungabili, nel senso che il limite esiste, ma viene a cadere l’unicità: tutte le linee appartenenti all’integrale generale passano per l’origine, dove possono essere intese come soluzioni solo in senso esteso, in quanto i limiti per x → 0 dei due membri sono uguali. (Si vedano anche le voci: → equazione differenziale lineare; → equazione differenziale lineare, integrale di una).

• Equazione di Bernoulli. È un’equazione differenziale del tipo y′ = a(x)y + b(x)y ^α, con α ≠ 0, 1 (altrimenti l’equazione è lineare; si veda → Bernoulli, equazione differenziale di). Se α > 0, allora y ≡ 0 è un integrale, particolare se α > 1, singolare se 0 < α < 1. Dopo aver diviso per y ^α, la sostituzione z = y 1^−α trasforma l’equazione di Bernoulli nell’equazione lineare z’ = (1 −α)[a(x)z + b(x)]. Se ne ottiene la formula risolutiva

e y′ = y /x + x ²y ³ dà y = ±x[C + x]^−1/2

• Equazione omogenea (o di Manfredi). Un’equazione differenziale omogenea ha la forma y′ = ƒ(y /x). L’integrale generale è dato dalla formula

cui vanno eventualmente aggiunte le rette y = mx, con m soluzione dell’equazione ƒ(m) = m.

Per esempio, l’equazione differenziale y′ = 2y /x – y 3/x 3 ammette le rette y = 0, y = x, y = −x come integrali particolari, mentre l’integrale generale è dato da

che integrata fornisce (con un cambio della costante)

• Equazione differenziale esatta. Si tratta di un’equazione che si presenta nella forma

Pertanto, se la forma differenziale ω risulta chiusa in un dominio semplicemente connesso, cioè X_y = Y_x, allora ω è esatta, e, detto F(x, y) un suo potenziale, l’integrale generale dell’equazione differenziale è dato da F(x, y) = C. Per esempio, per l’equazione differenziale (x ² + y)dx + (x + y 2)dy = 0, definita in tutto il piano che è un dominio semplicemente connesso, si ha X_y = Y_x = 1, e dunque la forma è esatta e un suo potenziale è dato da F(x, y) = x ³/3 + xy + y 3/3 e dunque le soluzioni soddisfano l’equazione x ³/3 + xy + y 3/3 = C. (Si osservi che nel caso la forma differenziale non resti definita in un dominio semplicemente connesso, allora l’equazione differenziale ha senso localmente, per esempio nell’intorno del punto in cui si assegna il dato iniziale, e se è chiusa allora è anche localmente esatta.)

• Equazione di Riccati. È un’equazione che ha la forma y′ = p(x)y 2 + q(x)y + r(x). Per la ricerca dell’integrale generale di una equazione di questo tipo non esiste una formula risolutiva, a meno che non sia nota una sua soluzione particolare u(x). In tal caso l’integrale generale è dato da

con

• Equazioni riconducibili alle esatte. Se un’equazione differenziale scritta nella forma

_017.jpg>

non è esatta, è possibile che la si possa rendere tale moltiplicandola per un opportuno fattore (detto fattore integrante). Due casi in cui si può seguire questo procedimento sono quelli in cui il rapporto

dipende dalla sola x, nel quale il fattore integrante è

e quello in cui

dipende solo da y, in cui si deve moltiplicare per

Per esempio, l’equazione differenziale (xy + y 2 +y)dx + (x + 2y)dy = 0 non è esatta, essendo X_y = x + 2y + 1 ≠ Y_x = 1. Tuttavia la differenza X_y − Y_x = x + 2y è uguale a Y, per cui il loro rapporto è la funzione costante g(x) = 1. Ne segue che moltiplicando per μ(x) = e^x si ottiene un’equazione esatta, il cui integrale generale è dato da e^x(xy + y 2) = C.

Equazione differenziale del primo ordine in forma non normale

Tra le equazioni in forma non normale si segnalano le seguenti:

• Equazione di Clairaut. Una equazione differenziale di questo tipo ha la forma y = xy′ + ƒ(y′ ) (→ Clairaut, equazione differenziale di). L’integrale generale è dato dalla famiglia di rette y = Cx + ƒ(C) cui va aggiunto l’integrale singolare rappresentato dal loro inviluppo, e ottenuto dal sistema

Per esempio, l’equazione differenziale y = xy′ + (y′ )2 ammette come integrale generale le rette y = Cx + C ², e come integrale singolare la parabola y = −x ²/4.

• Equazione di Lagrange. Un’equazione differenziale di questo tipo ha la forma y = xg(y′ ) + ƒ(y′ ). Costituisce una generalizzazione del caso precedente, e ammette l’integrale generale (in forma parametrica)

con

più l’eventuale inviluppo, ottenuto eliminando C dal sistema

• Equazione risolta rispetto a y. Un’equazione differenziale di questo tipo ha la forma y = ƒ(x, y′ ). Derivando si ottiene y′ = ƒ_x (x, y′) + ƒ_y (x, y′ )y″, del secondo ordine, ma mancante della y (si veda oltre). Una volta ottenuta la soluzione nella forma y′ = z(x, C), l’integrale generale è y = ƒ(x, z(x, C)).

• Equazione risolta rispetto a x. Un’equazione differenziale di questo tipo ha la forma x = ƒ(y, y′). Assumendo x = x(y) ⇒ x′ = 1/y′ si ha l’equazione x = ƒ(y, 1/x′ ) del tipo precedente.

• Equazione del primo ordine e di secondo grado. Un’equazione differenziale di questo tipo (la parola grado si riferisce alla struttura algebrica dell’equazione, mentre la parola ordine si riferisce a quella differenziale) ha la forma α(x, y)(y′ )² + β(x, y)y′ + γ(x, y) = 0. Nei punti in cui il discriminante Δ = β² − 4 αγ dell’equazione di secondo grado in y′ è positivo, l’equazione “si spezza” in due equazioni del primo ordine in forma normale che, se di tipo noto, possono essere portate alle quadrature. In ogni caso, ove Δ > 0, il problema di Cauchy ammette due soluzioni.

Equazioni differenziali di ordine superiore

Tra le equazioni di ordine superiore si segnalano le seguenti:

• Equazione in cui non compare la variabile dipendente y. Un’equazione differenziale di questo tipo ha la forma F(x, y′, y″ ) = 0. Ponendo z(x) = y′ (x) l’equazione diviene del primo ordine, ed è trattata come nei punti precedenti. Trovata z = z(x, C), un’integrazione permette di risalire alla y. Va sottolineato che questa seconda integrazione può assumere espressioni analitiche diverse in dipendenza della costante C. Per esempio, l’equazione y″ − 2x(y′ )² = 0 dà l’equazione a variabili separabili z’ = 2xz ², che fornisce, oltre all’integrale particolare z = 0, l’integrale generale y′ = z = 1/(C − x ²). L’integrazione di tale funzione dipende dal segno di C:

• Equazioni in cui non compare la variabile indipendente x (equazioni autonome). Un’equazione di questo tipo ha la forma F(y, y′, y″ ) = 0. Se F(y0, 0, 0) = 0, allora y = y0 è un integrale particolare. Altrimenti, assumendo y come variabile indipendente e posto y′ = p(y), si ha y″ =p(y)p′ (y) e l’equazione si trasforma in una equazione del primo ordine nell’incognita p(y). In particolare le equazioni della forma y″ = ƒ(y) ammettono l’integrale primo (y′ )²/2 = F(y) + C, con F primitiva di ƒ. Questo caso particolare è importante perché rappresenta la conservazione dell’energia. Infatti, se la variabile indipendente è il tempo t, la grandezza y″ è l’accelerazione e l’equazione traduce il secondo principio della dinamica. Nell’integrale primo, (y′ )²/2 rappresenta l’energia cinetica, F(y) il potenziale della forza esterna per unità di massa ƒ(y). Per esempio, l’equazione del pendolo y″ = −gsiny dà (y′ )²/2 = gcosy + C. Questa è a variabili separabili, anche se l’integrale che se ne ottiene non è elementare.