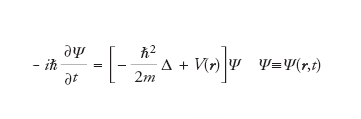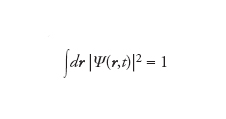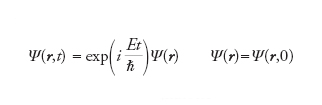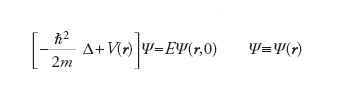equazione di Schrödinger
equazione di Schrödinger
Equazione fondamentale della meccanica quantistica non relativistica. Nel semplice caso di una sola particella in presenza, nello spazio tridimensionale, di una forza conservativa cui è associata l’energia potenziale V(r), tale equazione si scrive
dove i è l’unità immaginaria, ℏ è la costante di Planck ridotta, m è la massa della particella, r è la coordinata nello spazio tridimensionale, t è la variabile temporale, e la funzione d’onda Ψ(r,t) caratterizza il comportamento della particella in questione, in quanto il suo modulo quadrato, rappresenta la densità di probabilità che tale particella si trovi nel punto r al tempo t. Ciò naturalmente richiede che tale funzione soddisfi la condizione di normalizzazione
dove l’integrazione è estesa a tutto lo spazio, che corrisponde all’ovvia osservazione che la probabilità che la particella si trovi in qualche punto dello spazio è pari all’unità. Tale condizione è compatibile con l’equazione di Schrödinger, cioè, se vale al tempo iniziale t=0, l’evoluzione temporale ne garantisce sempre la validità. L’equazione (temporale) di Schrödinger è inoltre compatibile con la riduzione
Et
che implica che la funzione Ψ(r) soddisfi l’equazione ‘stazionaria’ di Schrödinger,
Le autofunzioni normalizzabili Ψν(r), soluzioni di questa equazione, corrispondono agli stati legati della particella nel potenziale V(r); generalmente esistono solo per valori discreti (quantizzati) Eν dell’energia. Solo soluzioni di questo tipo hanno significato fisico nel caso di potenziali (‘confinanti’) che divergono positivamente a grandi distanze. Nel caso di potenziali che si annullano abbastanza rapidamente a grandi distanze, è invece possibile attribuire un significato anche a soluzioni non divergenti ma non normalizzabili, che risultano associate a processi di diffusione sul potenziale in questione corrispondenti schematicamente a esperimenti in cui un fascio di particelle viene diretto da lontano sul potenziale (per ipotesi localizzato, in quanto si annulla all’infinito); si misurano poi le particelle diffuse a grande distanza, dove il potenziale è praticamente nullo. L’estensione dell’equazione di Schrödinger al caso di molte particelle è concettualmente semplice, ma diventa in tal caso molto più difficile estrarre da tale equazione, mediante una trattazione teorica, risultati confrontabili con l’esperimento; cosa ben comprensibile, poiché tale equazione descrive, in linea di principio, l’enorme varietà di fenomeni che caratterizzano la fisica e la chimica non relativistiche, cioè gran parte della fenomenologia del mondo che ci circonda.
→ Solitoni