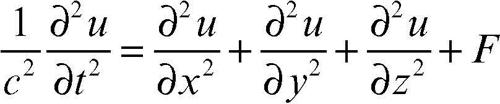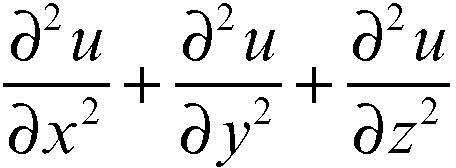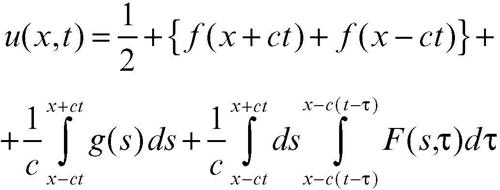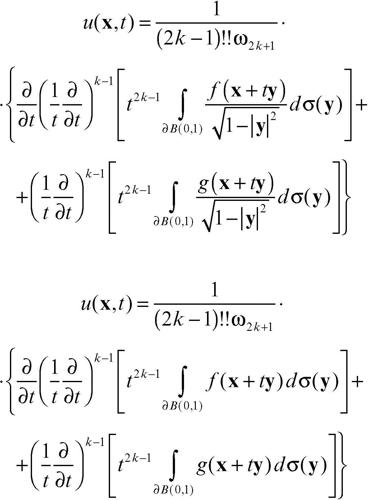Alembert (d'), equazione di
Alembert (d'), equazione di
Alembert (d’), equazione di equazione differenziale del secondo ordine alle derivate parziali detta anche equazione delle onde, in quanto costituisce un modello matematico per i moti ondosi. Nel caso generale, l’equazione ha come incognita la funzione u(x, y, z, t) e la sua espressione è:
L’espressione
che può essere indicata con ∇2, essendo ∇ l’operatore nabla, è detta operatore di Laplace ed è spesso indicata con ∆. Si può allora riscrivere l’equazione precedente in modo sintetico introducendo un ulteriore operatore, detto operatore di d’Alembert o operatore dalembertiano
L’equazione delle onde diventa così:
Si tratta di una equazione differenziale alle derivate parziali di tipo iperbolico, che descrive la propagazione ondosa in mezzi omogenei e isotropi. La costante c rappresenta la velocità di propagazione dell’onda e la funzione F le forze esterne che agiscono sul sistema. Nei casi monodimensionale e bidimensionale questa equazione viene anche detta rispettivamente equazione della corda vibrante o della membrana vibrante corrispondentemente al fenomeno fisico che essa descrive.
Nel caso monodimensionale, u(x, t) è la funzione incognita e rappresenta lo spostamento di un punto della corda tesa in direzione normale alla corda stessa, x indica la distanza del punto da uno degli estremi della corda, t indica il tempo e c la velocità di propagazione dell’onda sulla corda.
L’integrale generale dell’equazione monodimensionale omogenea (quindi con F = 0) è
dove φ e ψ sono funzioni arbitrarie di una variabile. I due termini rappresentano rispettivamente una perturbazione che avanza (onda progressiva) e una che regredisce (onda retrograda) lungo l’asse x, con velocità di propagazione c.
La soluzione del problema di → Cauchy u(x, 0) = ƒ(x), ut(x, 0) = g(x), è data dalla formula:
dove l’ultimo termine rappresenta il contributo delle forze esterne F, valutato con un integrale doppio esteso al dominio di dipendenza (→ equazioni differenziali alle derivate parziali); il dominio di dipendenza è il triangolo individuato dalle caratteristiche uscenti dal punto (x, t), che sono le rette di rispettivo coefficiente angolare ±1/c e la linea portante i dati, cioè l’asse t = 0.
La formula risolutiva, per i casi di dimensione n = 2k e n = 2k + 1, e per c = 1, diviene rispettivamente:
La differenza tra i casi con n pari o dispari è significativa: infatti in questi ultimi la soluzione in un punto (x0, t0) dipende solo dai dati iniziali sulla superficie sferica di equazione |x − x0| = t0 (principio di Huygens, dal nome del fisico e matematico olandese Ch. Huygens, mentre per n pari essa dipende dai valori su tutta la superficie individuata da |x − x0| ≤ t0. Il caso pari si ottiene da quello dispari con il cosiddetto metodo della discesa, che consiste nel notare che una soluzione (2k + 1)-dimensionale, che non dipende da una variabile, è anche soluzione del corrispondente problema 2k-dimensionale (→ onda).