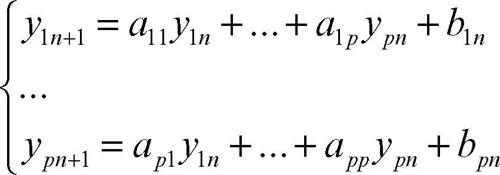equazione alle differenze
equazione alle differenze
equazione alle differenze o equazione alle differenze finite, equazione della forma
in cui l’incognita è una successione {yn}. Soluzione dell’equazione alle differenze è ogni successione tale che tutti i suoi elementi verificano l’equazione stessa. Un’equazione alle differenze appare la variante discreta di un’equazione differenziale. Tale equazione è detta di ordine r se effettivamente in essa compaiono entrambi i valori di yn+r e yn, giacché ordine di un’equazione alle differenze è la differenza tra l’indice più alto e l’indice più basso degli elementi che vi figurano.
Nel caso di un’equazione alle differenze nella forma normale yn+r = ƒ(yn+r, yn+r−1, ..., yn, n) la conoscenza degli r valori iniziali y0, y1, ..., yn+r−1 permette per ricorrenza la conoscenza dell’intera successione, purché la funzione ƒ risulti sempre calcolabile per i successivi valori degli argomenti. Nel caso di un’equazione alle differenze lineare, cioè della forma ar(n)yn+r + ar−1(n)yn+r−1 + ... + a0(n)yn = b(n), vale il principio di sovrapposizione (→ equazione differenziale), per cui la soluzione generale si ottiene sommando alla soluzione generale dell’equazione omogenea associata, calcolata ponendo b(n) = 0, una soluzione particolare dell’equazione completa, che nei casi più comuni può essere trovata con un particolare metodo detto metodo dei coefficienti indeterminati. Tale metodo rappresenta un tentativo mirato, in cui si cerca una soluzione in una forma che si ritiene corretta (per esempio, un polinomio) nella quale sono incogniti solo alcuni coefficienti che si determinano imponendo che la soluzione soddisfi l’equazione. La soluzione generale dell’equazione omogenea ha poi la forma
dove uk,n sono r soluzioni indipendenti dell’equazione stessa e ck sono costanti arbitrarie. La verifica dell’indipendenza si può eseguire controllando che il loro determinante di → Casorati sia diverso da 0. La determinazione delle soluzioni uk,n è possibile nel caso delle equazioni a coefficienti costanti, nelle quali cioè gli ak non dipendono da n. Scritto infatti il polinomio caratteristico
l’equazione assume la forma simbolica P(E)yn = 0, dove E è l’operatore di traslazione Eyn = yn+1. L’equazione ottenuta uguagliando a 0 il polinomio caratteristico P(γ) = 0 è detta equazione caratteristica dell’equazione omogenea; a ogni sua soluzione λj corrisponde la soluzione
Se la radice λj ha molteplicità m, anche
sono soluzioni. Nel caso di radici complesse coniugate, le si scrive nella forma trigonometrica λ = ρ (cosθ ± isinθ) ottenendo le soluzioni ρncos(nθ) e ρnsin(nθ); se le radici sono multiple, le si moltiplica per gli stessi fattori nk del caso reale. Per esempio, l’equazione
ammette la soluzione generale
L’equazione yn+2 − 2yn+1 + 4yn = 0 dà
Nel caso di sistemi di equazioni lineari di primo ordine a coefficienti costanti di tipo normale, della forma
dove i coefficienti aij e le p successioni {b1n}, ..., {bpn} sono assegnati, mentre le p successioni {y1n}, ..., {ypn} sono incognite (caso al quale possono essere ricondotti, mediante opportune sostituzioni, sistemi di ordine qualsiasi), sono gli autovalori e gli autovettori della matrice dei coefficienti a determinare completamente la natura e le proprietà delle soluzioni.