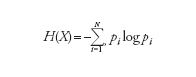entropia della sorgente

entropia della sorgente

Denotata con il simbolo H(X), rappresenta la quantità media di informazione associata a una sorgente discreta che genera N simboli indipendenti X_ι con probabilità p_ι (i=1,…,N) e può essere definita come

dove il logaritmo si intende in base 2 per sorgenti binarie (in tal caso H si misura in bit). Se la sorgente emette segnali continui, con una distribuzione di probabilità p(x), per il calcolo dell’entropia della sorgente occorre sostituire la sommatoria con il relativo integrale. Occorre notare che, sebbene dalla definizione data possa sembrare che H sia una funzione di X, in realtà essa risulta funzione della probabilità della sorgente (legata alla variabile aleatoria X) ed è pertanto un numero. Poiché si ha generalmente a che fare con processi a banda limitata, è possibile ricondursi al solo caso di processi aleatori tempo-discreti {X_ι}, con i∈(−∞,+∞), e considerare una sorgente discreta senza memoria, nella quale i simboli X_ι, che assumono valori sull’alfabeto A={a_ᾡ,a_ᾠ,…,a_Ν}, sono generati in modo indipendente e con la stessa distribuzione. Nel caso di una sorgente simmetrica binaria, per es., risulta A={0,1} e p(X_ι=1)=1−p(X_ι=0)=p=0,5. Lo studio sistematico dell’entropia all’interno della teoria dell’informazione si deve al lavoro di Claude Shannon alla fine degli anni Quaranta del secolo scorso. La definizione di entropia data, come espressione del livello di informazione di una sorgente, può ricavarsi sulla base di considerazioni intuitive. Osservando un semplice processo stocastico, per es., studiando il legame tra condizioni meteorologiche e inquinamento dell’aria in una data area geografica, si può definire l’alfabeto A come l’insieme delle combinazioni condizione meteo-livello di inquinamento (per es., caldo-molto inquinato, freddo-poco inquinato, e così via). Raccolti i dati, non è difficile giungere alle seguenti conclusioni: (a) il contenuto informativo della variabile a_Ϛ dipende soltanto dalla sua probabilità p_Ϛ (e non dal suo valore) e viene pertanto definita come auto informazione I(p_Ϛ); (b) l’autoinformazione I(·) è una funzione continua e decrescente del suo argomento; (c) se p_Ϛ=p^(Ϛ)−p^(ϰ) allora I(p_Ϛ)=I(p^(Ϛ))+I(p^(ϰ)). Shannon trovò che l’unica funzione che soddisfa tutte le precedenti condizioni è quella logaritmica (indipendentemente dalla sua base). Poiché l’informazione associata a ogni simbolo emesso dalla sorgente a_ι è dunque pari alla sua autoinformazione I(p_ι)=−logp_ι, l’informazione associata all’intera sorgente sarà pari alla media ponderata dell’autoinformazione associata a tutti i simboli, dove i pesi sono rappresentati dalle loro corrispondenti probabilità. Il concetto di entropia della sorgente ha un’importante applicazione nell’ingegneria dei sistemi di comunicazione. Secondo la teoria di Shannon, infatti, dato un sistema di comunicazione con sorgente, canale e osservatore assegnati, per fornire all’osservatore, con la precisione desiderata, l’informazione generata dalla sorgente e degradata dalla presenza del rumore sul canale, occorre ottimizzare codificatore (in fase di trasmissione) e decodificatore (in fase di ricezione). Il primo elimina la ridondanza dalla successione di simboli emessi dalla sorgente (aggiungendo nuovi simboli ridondanti per la protezione contro i disturbi); il secondo compie le operazioni inverse, con lo scopo di ricostruire il segnale generato dalla sorgente (o una sua stima). Secondo la teoria di Shannon, data una sorgente di entropia H e un canale di capacità C sul quale transita l’informazione generata dalla sorgente, se H〈C è possibile teoricamente progettare un codificatore e un decodificatore che garantiscono all’osservatore di ricevere l’informazione generata dalla sorgente con una probabilità di errore per simbolo arbitrariamente piccola. Se invece H>C tale probabilità di errore non può scendere al di sotto di una quantità non nulla, comunque si progettino il codificatore e il decodificatore.

→ Sistemi di comunicazione wireless