emiedria
Enciclopedia on line
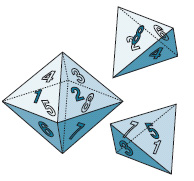
In cristallografia, operazione basata sul concetto di meroedria, consistente nel derivare geometricamente alcune forme semplici di un sistema da altre (oloedriche) dimezzandone il numero delle facce: il tetraedro, per es., si deriva dall’ottaedro per eliminazione di 4 facce alterne (v. fig., in cui l’ottaedro e i due tetraedri risultanti hanno le facce corrispondenti ugualmente numerate).