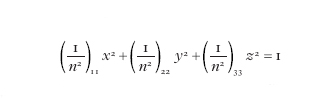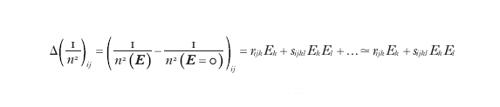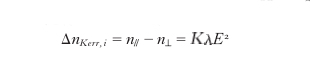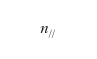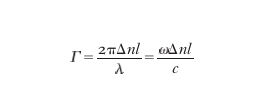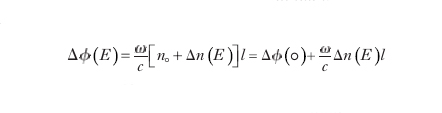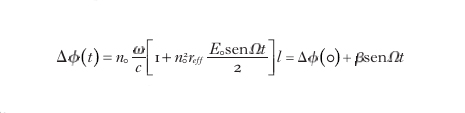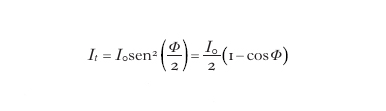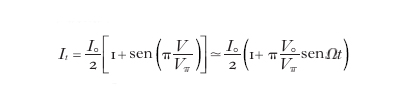Elettroottica
Elettroottica
L'e. è il settore delle scienze fisiche e dell'ingegneria che studia le relazioni tra fenomeni elettrici e luminosi, la modificazione delle proprietà ottiche della materia per effetto di correnti e campi elettrici, e dispositivi correlati quali laser, diodi emettitori di luce, modulatori elettroottici, fotorivelatori; in questa accezione è sinonimo di optoelettronica. In senso più stretto, l'e. studia l'azione di un campo elettrico su emissione, assorbimento e propagazione della luce in mezzi materiali, che si manifesta specificamente negli effetti Stark e negli effetti elettroottici Kerr e Pockels; nella presente voce si limiterà la trattazione a questi ultimi.
Gli effetti Kerr (1875) e Pockels (1883) trattano la birifrangenza indotta da un campo elettrico applicato a un dielettrico trasparente, fenomeno noto anche come elettrorifrazione. La dipendenza dal campo è lineare nel caso dell'effetto Pockels, quadratica per l'effetto Kerr. Nei cristalli l'applicazione di un campo elettrico provoca la distorsione degli orbitali elettronici e, in alcuni casi, una lieve alterazione del reticolo cristallino, con conseguente modificazione dei livelli energetici del sistema e della risposta dielettrica. In materiali isotropi, come liquidi o gas, l'effetto Kerr, l'unico presente, è per lo più associato all'allineamento delle molecole indotto dal campo elettrico, per cui il mezzo si comporta otticamente come un cristallo uniassico, con l'asse ottico nella direzione del campo applicato.
Gli effetti elettroottici possono essere utilizzati per modulare fase, stato di polarizzazione e ampiezza di un campo ottico propagantesi nel materiale; i dispositivi utilizzati prendono il nome di cella di Pockels e cella di Kerr.
Le celle di Pockels sono largamente utilizzate in optoelettronica, grazie alle elevate prestazioni su un intervallo di lunghezze d'onda che si estende dall'ultravioletto all'infrarosso, in particolare per modulare radiazione laser, sia internamente sia esternamente al risonatore. Per applicazioni alle comunicazioni ottiche hanno grande importanza i modulatori elettroottici in guida d'onda (che impiegano come materiali LiNbO3 e GaAs), i quali possono raggiungere frequenze di modulazione di decine di GHz con tensioni di pilotaggio di pochi volt. Le celle di Kerr, a causa degli alti valori capacitivi e della limitata risposta alle alte frequenze dovuta ai tempi di rilassamento molecolari, che nel caso di liquidi spesso non supera la decina di megahertz (solo in alcuni casi, per es. CS2, raggiunge ∼1GHz), sono scarsamente impiegate.
La propagazione della radiazione ottica in un materiale trasparente può essere in generale descritta in termini del tensore permettività dielettrica, εij (i,j=1,2,3), o del suo inverso, 1/εij=(1/n2)ij, dove n è l'indice di rifrazione. Gli elementi di tali tensori, simmetrici per tutte le classi cristallografiche e per ogni orientazione degli assi dielettrici, nei dielettrici omogenei, non magnetici e privi di perdite sono tutti reali. Lo studio della propagazione fa uso di una rappresentazione matematica, l'ellissoide degli indici di rifrazione che, riferito agli assi dielettrici principali, assume la forma canonica
L'applicazione di un campo elettrico E modifica la risposta dielettrica del mezzo, causando una variazione degli elementi del tensore (1/n2)ij con una trasformazione dell'ellissoide degli indici (rotazione degli assi e variazione delle lunghezze), data da
dove rijk e sijkl sono, rispettivamente, i coefficienti del tensore elettroottico lineare rappresentabile, per simmetria di permutazione, da una matrice in forma contratta (6×3), e del tensore elettroottico quadratico, rappresentabile con una matrice in forma contratta (6×6). I coefficienti rijk hanno valori dell'ordine dell'inverso del campo elettrico interno al materiale agente sugli elettroni, r∼10−11 m/V; i coefficienti sijkl hanno valori dell'ordine dell'inverso del quadrato del campo elettrico interno, s∼10−22 m2/V2. Essendo i campi elettrici applicati molto inferiori a quello interno, l'effetto lineare risulta predominante; esso è presente, tuttavia, solo in materiali che non posseggono simmetria di inversione. Nelle undici classi di simmetria che hanno centro di inversione (materiali centrosimmetrici), i coefficienti rij sono identicamente nulli e l'effetto Kerr, sempre presente, diventa dominante. A causa della dispersione del materiale e del suo tempo di risposta (variabile, a seconda dei meccanismi implicati, da 10−6 a 10−14 s), i coefficienti elettroottici dipendono dalla lunghezza d'onda e dalla frequenza del campo elettrico applicato.
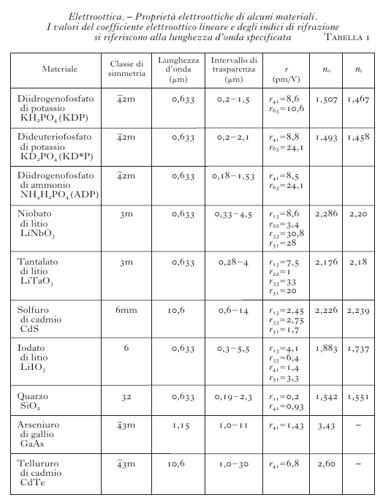
Fissata una definita direzione di propagazione dell'onda nel mezzo, la birifrangenza indotta Δn, data dalla differenza tra gli indici di rifrazione relativi ai due autostati di polarizzazione lineare consentiti, oscillanti in due direzioni mutuamente ortogonali e normali alla direzione di propagazione, è esprimibile come ΔnPockels=n03reffE/2 e ΔnKerr=n03seffE2/2, dove n0 è l'indice di rifrazione ordinario e i coefficienti elettroottici efficaci reff e seff sono legati agli elementi del relativo tensore elettroottico. I valori dei coefficienti elettroottici lineari per alcuni cristalli sono riportati in tab. 1. Nell'effetto Kerr in mezzi isotropi, la birifrangenza è espressa come
,
dove
e
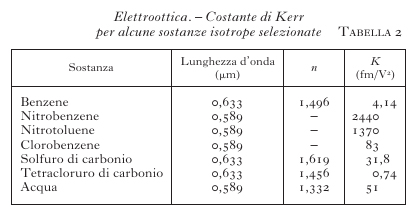
sono gli indici di rifrazione per luce polarizzata parallelamente e ortogonalmente al campo E, e K, funzione del materiale e della lunghezza d'onda λ, è la costante di Kerr. In tab. 2 sono riportati i valori di K per alcune sostanze.
Il ritardo elettroottico Γ che si viene a generare tra i due autostati di polarizzazione è dato da
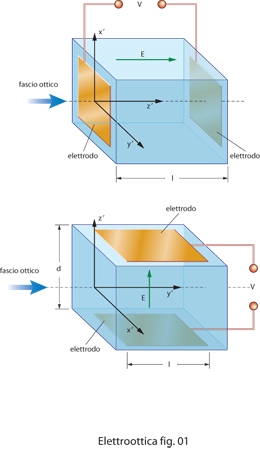
dove λ è la lunghezza d'onda della luce nel vuoto, l la lunghezza d'interazione nel materiale, ω la frequenza angolare della radiazione, e c la velocità della luce nel vuoto. Nell'effetto Pockels si ha Γ=π(V/Vπ); nell'effetto Kerr, Γ=π(V/Vπ)2, dove V è la tensione applicata al materiale e Vπ, detta tensione di mezz'onda, è un parametro dipendente dalle proprietà ottiche del mezzo, da λ e, nel caso di configurazione trasversale, dalle dimensioni della cella. Il campo elettrico può essere applicato in direzione parallela a quella di propagazione della luce o perpendicolare a essa, realizzando un modulatore in configurazione longitudinale o trasversale (fig. 1). Nella prima, impiegata solo con celle di Pockels, i valori di Vπ sono elevati e variano all'incirca tra 1 kV e 10 kV per radiazione nel visibile; è inoltre necessario utilizzare elettrodi a corona anulare o realizzati con materiali conduttivi trasparenti. Nella più vantaggiosa configurazione trasversale, Vπ assume valori sensibilmente più bassi, dalla decina di volt a ∼l kV, e gli elettrodi per applicare tensione al cristallo non interferiscono con il percorso del fascio ottico.
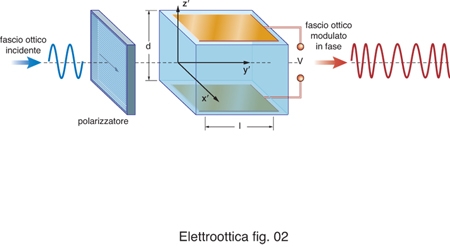
Nei modulatori di fase, che possono adottare ambedue le configurazioni, è essenziale che la polarizzazione lineare del fascio incidente sia parallela a uno degli assi dielettrici principali del cristallo in presenza di campo elettrico (fig. 2). In tal modo lo stato di polarizzazione, coincidendo con un autostato all'interno del cristallo, non viene modificato. Il ritardo di fase all'uscita del modulatore è dato da:
dove n0 è l'indice di rifrazione (ordinario) in assenza di campo elettrico. La fase del campo ottico incidente risulta modulata in uscita se il campo elettrico ha una dipendenza temporale. Per es., considerando una cella di Pockels e una modulazione sinusoidale del campo elettrico E=E0senΩt, si ha
dove β è l'indice di modulazione di fase espresso in radianti e Ω la frequenza angolare del campo elettrico modulante.
Nei modulatori di polarizzazione il cristallo elettroottico si comporta come una lamina ritardatrice variabile. Un filtro polarizzatore in ingresso seleziona lo stato di polarizzazione lineare del campo ottico incidente; i due autostati di polarizzazione ortogonali che si propagano nel modulatore subiscono un ritardo elettroottico di fase Γ dipendente dal campo elettrico applicato. In uscita dalla cella i due autostati si ricombinano dando luogo a un'onda con polarizzazione in generale ellittica, variabile con continuità tra due stati limite in funzione della tensione applicata. Il modulatore può essere realizzato sia in configurazione longitudinale sia trasversale.
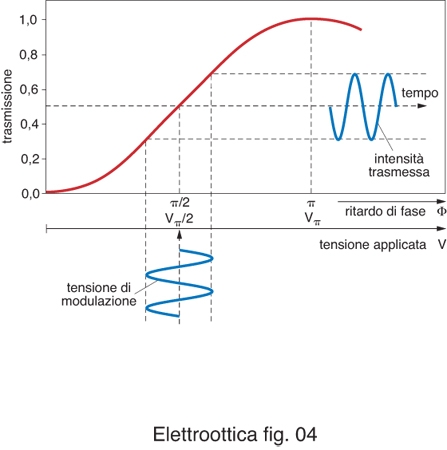
Al fine di modulare l'intensità di un fascio di radiazione è necessario inserire la cella tra due filtri polarizzatori incrociati, i cui assi di trasmissione sono ruotati di 90° l'uno rispetto all'altro e non coincidono con un asse dielettrico principale (per es., con riferimento alla cella nella fig. 1 in basso, formano un angolo di 45° con x' e z').In questa configurazione la modulazione di polarizzazione è convertita in modulazione di ampiezza del campo ottico; l'intensità della radiazione trasmessa It è legata a quella della radiazione incidente I0 dalla relazione
dove Ö è il ritardo di fase totale, somma del ritardo elettroottico Γ e di quello dovuto alla birifrangenza intrinseca del materiale Ö0, sempre nulla per un mezzo Kerr. Per ottenere un'efficiente modulazione è opportuno adoperare il modulatore nella zona lineare della sua caratteristica, in un intorno di Ö=π/2 (fig. 3), inserendo una lamina birifrangente a quarto d'onda sul cammino del fascio (per es., tra il modulatore e il filtro analizzatore in uscita) o applicando al modulatore una tensione pari a Vπ/2 per ottenere un ritardo di fase aggiuntivo di π/2. Considerando una cella di Pockels, si ottiene in tal caso una dipendenza lineare della trasmissione dalla tensione applicata:
avendo postoV=V0senΩt, con V0≪Vπ. Le celle elettroottiche hanno un comportamento di tipo capacitivo che può ridurne la banda di modulazione, comunque limitata dall'inverso del tempo di transito della luce nel modulatore a valori di alcuni gigahertz (Ωmax≃2πc/nl). È possibile superare tale limite adottando la configurazione trasversale a onda viaggiante, in cui il campo elettromagnetico modulante si propaga collinearmente con quello ottico nel cristallo; si raggiungono in tal caso frequenze di modulazione fino a ∼100 GHz.
bibliografia
Handbook of optics. Devices, measurements, & properties, ed. M. Bass, 2° vol., New York 19952; A. Yariv, P. Yeh, Optical waves in crystals. Propagation and control of laser radiation, Hoboken (NJ) 2003.