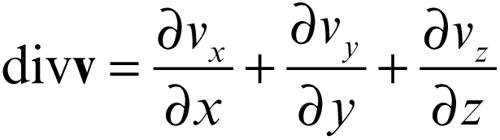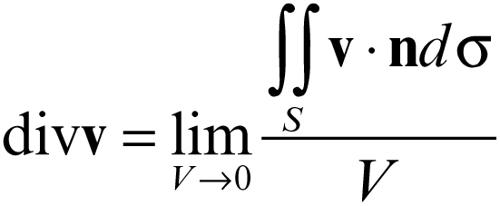vettore, divergenza di un

vettore, divergenza di un

vettore, divergenza di un in geometria differenziale e nelle applicazioni della matematica alla fisica, operatore differenziale che fa corrispondere a un vettore v una quantità scalare. La divergenza si indica con divv e viene definita dalla somma delle tre derivate parziali rispetto a x, y, z delle componenti v_x, v_y, v_z del vettore lungo gli assi coordinati:

L’operatore divergenza ha anche la seguente interpretazione che ne giustifica il nome: se si considera un volume V che contiene il punto nel quale si vuole calcolare la divergenza, questa è data dal limite per V che tende a 0 del rapporto tra il flusso del vettore attraverso la superficie S che racchiude V e il volume stesso:

Dal punto di vista fisico, la divergenza misura il tasso di variazione della densità associata al campo in un certo punto dello spazio. Per esempio, se v = v(x, y, z) è la velocità di un fluido al punto P(x, y, z), la sua divergenza esprime la densità di flusso del campo uscente dal punto P (cioè la velocità del cambiamento del volume per unità di volume di una porzione infinitesimale del fluido contenente P).

La divergenza è invariante rispetto a ogni cambiamento di riferimento. Se nel campo vettoriale in cui v è definito risulta in ogni punto divv = 0, si dice che tale regione è sede di un campo solenoidale. Il teorema della divergenza stabilisce che l’integrale di volume della divergenza di un vettore è uguale al flusso del vettore attraverso la superficie che racchiude il volume:

(→ Green, formule di).