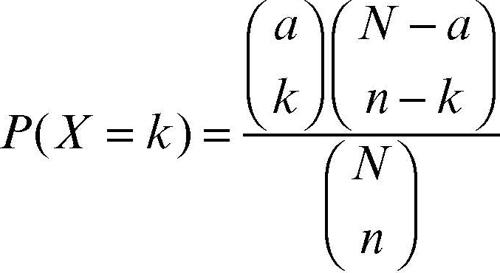distribuzione ipergeometrica

distribuzione ipergeometrica

distribuzione ipergeometrica distribuzione di probabilità di una variabile aleatoria discreta X sotto le seguenti condizioni:

• è dato un insieme di N elementi, di cui a elementi presentano una particolare caratteristica;

• si estraggono in blocco n tra gli N elementi (il che equivale a fare n successive estrazioni senza reimmissione);

• X esprime il numero di elementi, tra quelli estratti, che presentano la particolare caratteristica.

La funzione di distribuzione della probabilità è

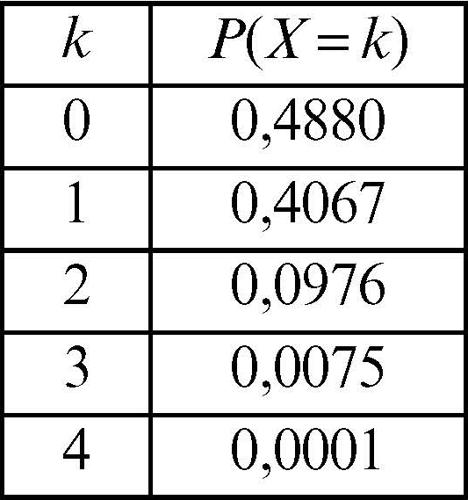
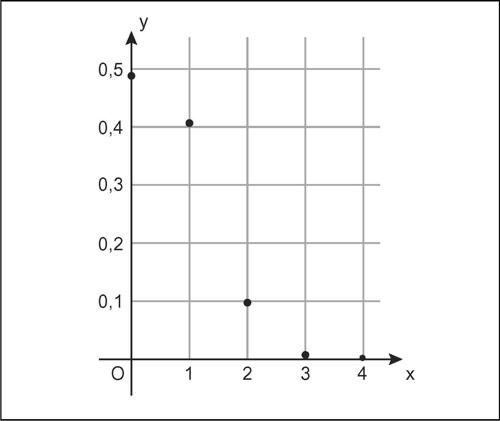
in cui i termini su due righe tra parentesi tonde sono coefficienti binomiali. In particolare, per n = 1 (cioè estraendo un solo elemento) si ritrova la probabilità p = a/N di estrarre proprio uno degli elementi (e quindi k = 1) che presenta la caratteristica che interessa. I parametri della distribuzione ipergeometrica sono dunque: N, numero di elementi dell’insieme da cui si effettua l’estrazione; n, numero degli elementi estratti; p, rapporto tra il numero a di elementi aventi la caratteristica d’interesse e N. Una variabile con tale distribuzione è perciò anche indicata con H(N, n, p). Per esempio, in un mazzo di N = 32 carte da poker, può interessare la caratteristica che tali carte siano degli assi. Poiché gli assi sono quattro, a = 4, e poiché si ricevono in blocco n = 5 carte, la probabilità di ricevere esattamente X = 0, X = 1, ..., X = 4 assi è distribuita secondo la tabella:

La media e la varianza di una variabile aleatoria X con distribuzione ipergeometrica di parametri N, n e p sono rispettivamente