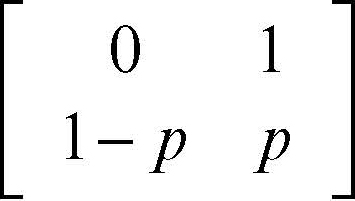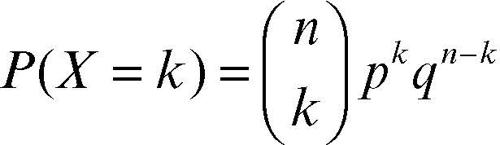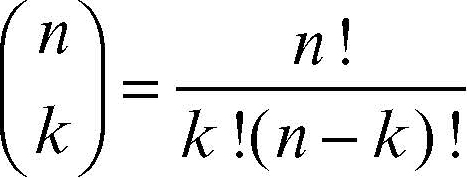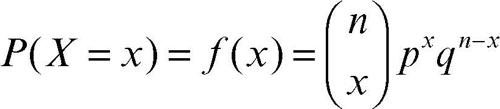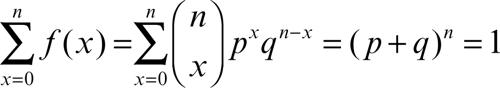distribuzione binomiale
distribuzione binomiale
distribuzione binomiale o distribuzione di Bernoulli, distribuzione di probabilità di una → variabile binomiale in un insieme di n prove indipendenti. Data una variabile aleatoria di Bernoulli, associata a uno spazio di due soli eventi tra loro complementari, l’uno con probabilità 0 < p < 1 e l’altro con probabilità q = 1 − p, si possono indicare i due eventi (successo/fallimento oppure sì/no) con 1 (per esempio, il successo) e 0 (per esempio, il fallimento). Per «successo o insuccesso» si può intendere qualunque situazione a due soli valori o nella quale interessi stabilire la presenza o l’assenza di un carattere (sano/malato, femmina/maschio, testa/croce, fumatore/non fumatore). Si ha così una variabile aleatoria dicotomica:
Si considerano quindi n prove o esperimenti indipendenti per rilevare il numero dei successi: per esempio, n successivi lanci di una moneta (in cui ogni volta p = q = 1/2) oppure n contemporanei lanci di dadi in cui sia considerato successo l’uscita di un numero minore di 3 (per ogni dado p = 1/3, q = 2/3). In una successione del genere si considera la variabile binomiale X = «numero di successi in n prove», che può assumere valori da 0 a n. La probabilità che, su n prove indipendenti, si abbiano k successi (con k ≤ n) è fornita dal teorema della distribuzione binomiale (o delle prove ripetute) ed è data da
dove
è il coefficiente binomiale. La funzione di distribuzione di probabilità ƒ(x) della variabile binomiale è conseguenza immediata della formula precedente:
Tale variabile è di tipo discreto, in quanto assume un numero finito di n + 1 valori, e quindi la sua distribuzione ƒ(x) è una distribuzione di probabilità discreta, tale che:
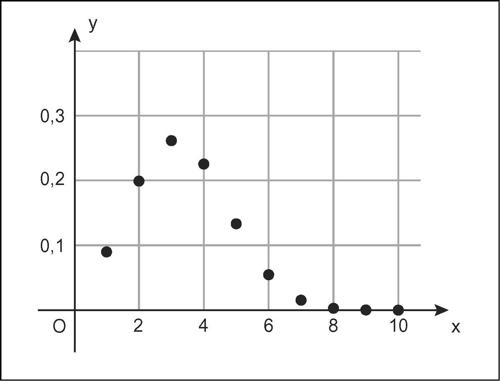
Parametri caratteristici di una distribuzione binomiale con probabilità p e numero di prove n (talvolta indicata con B(n, p) o Bin(n, p)) sono la media E(X) = np e la varianza Var(X) = npq. L’equivalente della moda in senso statistico, cioè il valore più probabile, è [(n + 1)p], in cui le parentesi quadre indicano la funzione parte intera. Se per esempio n = 10 e p = 1/3 si ha:
