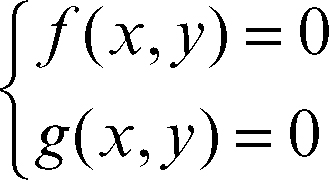problema, discussione di un

problema, discussione di un

problema, discussione di un in generale, per un problema geometrico o di altro tipo, determinazione delle condizioni o dei valori dei parametri presenti tra i dati per i quali il problema è impossibile, ha una sola soluzione oppure ha più soluzioni. La possibilità di risolvere un dato problema non dipende tanto dai particolari valori dei dati assegnati, quanto da quali sono i dati di cui si è a conoscenza. Si consideri per esempio il problema di determinare la lunghezza del lato di un quadrato di area 4. L’essere in grado di determinare la soluzione del problema è conseguenza non tanto del fatto che l’area del quadrato sia 4, ma del fatto che si conosce un metodo che, nota l’area del quadrato, permette di calcolarne il lato. Ciò suggerisce di analizzare il problema da un punto di vista più astratto e generale, non considerando più un quadrato di area 4, bensì un quadrato di area a, dove a è un simbolo che rappresenta un arbitrario numero non specificato a priori e che è detto parametro. Un parametro deve essere consistente con il problema considerato e non può in generale assumere valori del tutto arbitrari: esso è costretto a soddisfare delle condizioni, dette vincoli, che dipendono dal problema assegnato. Nel problema precedente, per esempio, il valore rappresentato da a, rappresentando la misura di una superficie, dovrà necessariamente essere non negativo. Assegnare un problema con parametro (o problema parametrico) significa che un dato del problema è supposto noto, ma non è specificato numericamente. Un problema con parametro costituisce perciò una classe infinita di problemi, ognuno dei quali è ottenuto assegnando valori costanti e determinati ai parametri coinvolti.

Discussione di un problema di secondo grado con parametro

La formalizzazione di un problema di secondo grado è un’equazione di secondo grado del tipo ƒ(x) = 0, dove ƒ è un polinomio nell’incognita x di secondo grado; se in essa è presente un parametro, un primo approccio al problema è fornito dalla discussione algebrica: tale approccio consiste nello studio del discriminante Δ (che in generale dipenderà dal parametro) dell’equazione di secondo grado ƒ(x) = 0: da esso dipende infatti l’esistenza di soluzioni reali del problema e il loro numero. Lo studio algebrico del discriminante determinerà pertanto condizioni sul parametro affinché esistano o meno soluzioni: per i valori del parametro per cui Δ è positivo, esisteranno due soluzioni reali distinte; per quelli per cui esso è nullo, esisteranno due soluzioni reali coincidenti; per quelli infine per cui esso è negativo, non esisteranno soluzioni reali. Tuttavia, tali soluzioni algebriche dovranno essere compatibili con i vincoli posti dal problema; in primo luogo, se si tratta di un problema geometrico, con il vincolo dato dal fatto che le misure di grandezze geometriche quali segmenti, angoli ecc. devono senz’altro essere non negative. Sia i vincoli geometrici intrinseci, sia quelli del particolare problema, determinano limitazioni al campo di variabilità delle incognite e, conseguentemente, definiscono quali delle soluzioni algebricamente possibili sono accettabili.

Un secondo approccio al problema è fornito dalla discussione grafica: si esprime il problema come un sistema del tipo

in cui solo una delle due equazioni contiene l’eventuale parametro. In questo modo ci si riporta all’intersezione tra una curva e una famiglia di curve (rappresentata dall’equazione contenente il parametro). Se il precedente sistema di equazioni è di secondo grado, il problema stesso costituisce un problema di secondo grado; in tale caso si cerca di riportarsi al caso di intersezione tra una parabola e un fascio di rette o, più in generale, tra una conica (per esempio, una circonferenza) e un fascio di rette. Con le condizioni intrinseche (l’essere per esempio un problema geometrico) e quelle esplicite poste dal problema (le relazioni che si hanno tra i dati) si limita il campo di variabilità delle incognite e, quindi, l’area di esame grafico del problema. Ci si ritroverà così a risolvere un sistema misto di equazioni e disequazioni nell’incognita x e si individuerà il numero di soluzioni che il problema può avere al variare del parametro.

Un terzo approccio per la discussione di un problema di secondo grado con parametro è quello che va sotto il nome di metodo di → Tartinville.