differenziale
differenziale
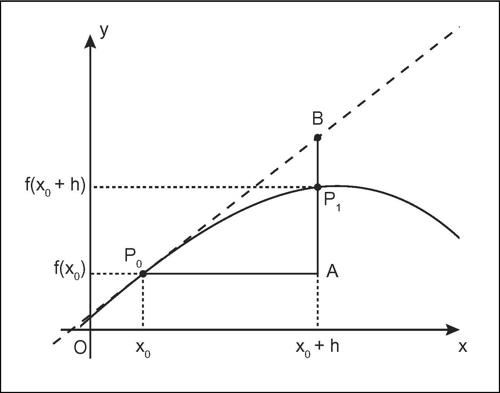
differenziale per una funzione ƒ(x) di una sola variabile, è indicato con df ed è il prodotto della derivata ƒ’′(x) per l’incremento dx della variabile indipendente. Dunque, df = ƒ′ (x)dx = ƒ′ (x)h, dove h è un sinonimo di dx, utile per evitare confusioni di senso. Infatti h è una variabile indipendente da x, mentre la scrittura dx potrebbe far pensare al contrario. Il differenziale è pertanto una funzione di due variabili, x e h, ma usualmente si considera x fissata, e quindi df funzione di h. In termini geometrici, il differenziale rappresenta l’incremento della funzione ƒ valutato lungo la tangente al suo grafico e non sul grafico stesso; df fornisce perciò la variazione dell’ordinata di un punto sulla retta tangente al grafico della funzione nel punto di ascissa x in corrispondenza della variazione dx dell’ascissa; è dunque la parte lineare dell’incremento Δƒ e differisce da esso per un infinitesimo di ordine superiore al primo rispetto all’incremento h: Δƒ = df + o(h).
Per funzioni di due variabili, l’interpretazione è analoga: il differenziale fornisce la variazione della terza coordinata di un punto situato sul piano tangente al grafico della funzione nel punto avente come prime coordinate x1, x2, in corrispondenza delle variazioni dx1, dx2 delle coordinate stesse. In generale, si conclude che sostituire in via di approssimazione il differenziale all’incremento della funzione trascurando l’infinitesimo di ordine superiore equivale geometricamente a sostituire, in prossimità del punto fissato, al grafico della funzione una porzione dal suo piano tangente. Il differenziale appare come prodotto formale dell’operatore di differenziazione d per la funzione f; d è definito, per funzioni ƒ(x) di una variabile, da hD, dove D è l’operatore di derivazione.
Il differenziale secondo è il differenziale del differenziale primo, cioè d 2 = dd = hD(hD) = h 2D 2, perché l’operatore di derivazione D agisce rispetto alla variabile x, il cui incremento h si comporta come una costante relativamente a D. Va sottolineato, per evitare errori, che le tre scritture dx 2, d(x 2) e d 2x rappresentano tre oggetti profondamente diversi. La prima, che dovrebbe essere scritta più correttamente come (dx)2, è il quadrato dell’incremento dx, che opportunamente è stato designato con l’unica lettera h. Si noti però che la scrittura senza parentesi compare nella notazione di Leibniz per la derivata seconda
ed è quindi storicamente consolidata. Il secondo, d(x 2), è il differenziale della funzione x 2, e vale dunque 2xdx. L’ultima espressione, d 2x, è il differenziale secondo della funzione x e poiché la derivata seconda di x è 0, si ha d 2x = 0.
Il differenziale primo gode della proprietà di invarianza rispetto a cambiamenti della variabile indipendente, nel senso che se si pone x = φ(t) il differenziale della funzione composta g(t) = ƒ (φ(t)) vale
Il differenziale secondo non è invece invariante rispetto a cambiamenti della variabile indipendente. Infatti:
ma questo secondo termine ora non è nullo perché x non è più la variabile indipendente.
Analogamente si introducono i differenziali successivi d n che sono definiti dalle potenze formali di d, ovvero d n = hnDn. Si parla così di ordine di un differenziale. Il differenziale n-simo di ƒ(x) è dato da hnƒ (n)(x) e, se questa derivata è diversa da zero, esso è un infinitesimo di ordine n rispetto all’incremento h. Determinazioni più precise dell’errore che si commette sostituendo df a Δƒ si ottengono con la formula di Taylor (→ Taylor, polinomio di), usandone i resti di Lagrange o di Peano; in tale formula intervengono anche il differenziale secondo e i differenziali di ordine superiore.
Per una funzione di più variabili, ƒ(x1, x2, …, xn), il differenziale df è ancora definito dalla relazione Δƒ = df + o(‖dx‖), e rappresenta la parte lineare di Δƒ, cioè l’incremento valutato lungo l’iperpiano tangente. Esso assume l’espressione df = p1dx1 + p2dx2 + … + pndxn, dove
sono le derivate parziali della funzione ƒ calcolate nel punto dato. I singoli addendi sono detti differenziali parziali, mentre la somma può essere designata, per chiarezza, come differenziale totale. Nel caso di più variabili la differenziabilità è però condizione più forte della semplice esistenza delle derivate parziali; una condizione sufficiente è data dalla continuità delle derivate parziali. Anche nel caso di funzioni di più variabili si definiscono i differenziali di ordine superiore (→ differenziazione; → Taylor, polinomio di). Nel caso di funzioni non regolari, si può estendere la nozione di differenziale introducendo il cosiddetto sottodifferenziale. La generalizzazione in spazi normati della nozione di differenziale corrisponde alla cosiddetta derivata di → Fréchet.