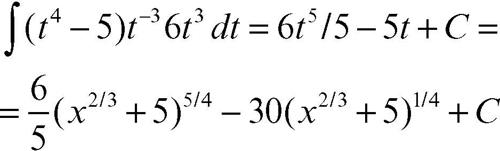differenziale binomio
differenziale binomio
differenziale binomio espressione della forma xm(axn + b)pdx, dove m = m1/m2, n = n1/n2, p = p1/p2 sono esponenti razionali e a, b sono parametri reali. È stato dimostrato da P.L. Čebišëv che un differenziale binomio ammette una primitiva elementare se e solo se uno dei tre numeri p, (m + 1)/n, (m + 1)/n + p è intero. Le sostituzioni che trasformano l’integrale di un differenziale binomio in quello di una funzione razionale sono rispettivamente, nei tre casi indicati:
In tutti gli altri casi l’integrale non è una funzione elementare. Queste sostituzioni permettono, nei casi indicati, l’integrazione di un differenziale binomio. Per esempio, l’integrale:
è calcolabile facilmente perché in esso si ha: m = 1/3, n = 2/3, p = −3/4, e quindi (m + 1)/n = 2, intero.
Quindi la sostituzione
rende l’integrale razionale. Infatti è t 4 = x 2/3 + 5 e, differenziando, 4t 3dt = 2/3x−1/3dx, da cui, scrivendo l’integrale nella forma
esso si trasforma in
