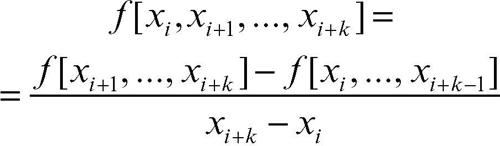differenze finite

differenze finite

differenze finite particolare sequenza di operazioni utilizzate soprattutto nei metodi numerici di calcolo approssimato, come la derivazione e l’interpolazione polinomiale. Sia dato un insieme di punti (nodi) {x_i}, i = 1, ..., k, e i corrispondenti valori ƒ(x_i) della funzione ƒ; si definisce, per ciascun punto, la differenza divisa di ordine zero come ƒ[x_i] = ƒ(x_i). La differenza divisa di ordine uno (o differenza divisa prima) è definita dal rapporto

Si possono quindi definire ricorsivamente le differenze divise di ordine k:

Se i punti sono equidistanti tra loro, x_i = x0 + ih, per i = 1, ..., k con h costante arbitraria, che assume il nome di passo nel particolare metodo usato, allora le differenze divise assumono un forma particolare e più semplice esprimibile attraverso le differenze finite. In generale, in analisi matematica si dice differenza finita di una funzione ƒ(x) l’incremento che la funzione subisce quando si passa da un valore x_i della sequenza di punti considerati al valore successivo x_i+1. Per ogni punto x_k, si definisce differenza finita di ordine zero la quantità Δ0ƒ(x_i) = ƒ(x_i), e la differenza finita prima Δ1ƒ(x_i) = ƒ(x_i+1) − ƒ(x_i). Analogamente alle differenze divise si definisce in generale differenza finita k-esima il termine Δ^kƒ(x_i) = Δ^k−1ƒ(x_i+1) − Δ^k−1ƒ(x_i). Si dimostra per induzione che, se il passo è h, la relazione tra le differenze divise e le differenze finite è tale che per ogni n:

I metodi di interpolazione polinomiale, come il metodo di → Newton e il metodo di → Lagrange, nei quali si approssima l’andamento locale di una funzione ƒ(x) con un polinomio di grado adeguato, utilizzano ampiamente le differenze finite e i polinomi interpolatori presenti nei due metodi sono definibili attraverso le differenze finite divise. Per esempio, utilizzando le differenze divise, il polinomio interpolatore della funzione ƒ nei punti x_i può essere espresso nella forma (detta di Newton)

Altri ambiti di utilizzo delle differenze finite sono costituiti dai vari metodi per l’approssimazione del valore della derivata di una funzione ƒ(x). Oltre alle differenze sin qui considerate, dette anche differenze finite in avanti, si trasformano differenze infinitesime in differenze finite divise secondo altre due modalità:

la derivata viene approssimata dalla differenza finita all’indietro, sostituendo al valore esatto della derivata il valore del coefficiente angolare della retta passante per il punto dato x_i e il punto precedente x_i−1;

la derivata viene approssimata dalla differenza finita centrale sostituendo al valore esatto della derivata il valore del coefficiente angolare della retta passante per il punto precedente x_i−1 e il punto successivo x_i+1 a quello dato.

Metodo alle differenze finite

Detto anche calcolo delle differenze finite, è lo studio delle variazioni dei valori di una funzione per effetto delle variazioni dei valori delle variabili indipendenti da cui la funzione stessa dipende. Con la locuzione metodo alle differenze finite si indica, in particolare, un metodo di approssimazione numerica della soluzione di un problema alle derivate parziali. Si rappresenta la funzione incognita, in due o più variabili, con l’insieme dei valori che essa assume in un opportuno insieme di punti del dominio di integrazione. Detti valori, opportunamente ordinati, saranno le incognite scalari del problema approssimante, non differenziale, che si vuole sostituire a quello differenziale dato. Il problema approssimante sarà perciò costituito da un sistema di equazioni non differenziali nelle incognite scalari, che si dovrà generare a partire dal problema differenziale di partenza, e quindi risolvere numericamente. Le equazioni differenziali alle derivate parziali di partenza esprimono una relazione, valida in tutti i punti del dominio di integrazione, tra la funzione incognita e le sue derivate parziali; essa sarà in particolare valida in ciascuno dei punti scelti opportunamente nel dominio di integrazione. Si potrà quindi scrivere una equazione per ciascun punto, e quindi per ciascuna incognita scalare introdotta, purché si sappiano esprimere, in funzione delle incognite scalari, le derivate parziali che compaiono (→ derivazione numerica).