diedro

diedro

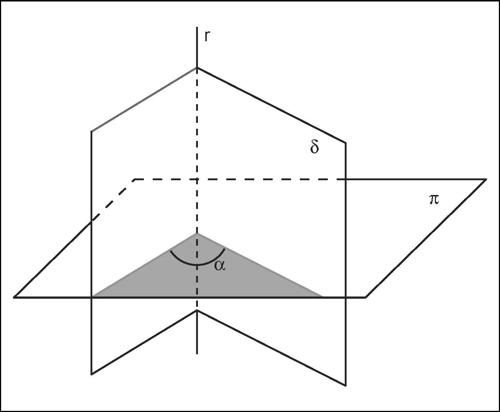
diedro in geometria, ciascuna delle due regioni in cui lo spazio tridimensionale viene diviso da due semipiani aventi per origine una stessa retta. I semipiani sono detti facce, la retta origine è detta spigolo. Un diedro si dice piatto se le sue facce appartengono a uno stesso piano, concavo se contiene i prolungamenti delle sue facce, convesso se non contiene tali prolungamenti. Si dice retto un diedro convesso avente le facce perpendicolari. Due piani che si intersecano formano quattro diedri, a due a due opposti allo spigolo e congruenti; in particolare due piani perpendicolari formano quattro diedri retti. Si dice sezione di un diedro l’angolo α ottenuto come intersezione del diedro con un piano π passante per lo spigolo r. Se π è perpendicolare allo spigolo r, l’angolo α è detto sezione normale del diedro con il piano π.

Tutte le sezioni normali di uno stesso diedro sono congruenti. L’ampiezza di un diedro è espressa dalla misura, in gradi o radianti, della sua sezione normale. Si dicono consecutivi due diedri che hanno in comune lo spigolo, una faccia e nessun altro punto. Si dicono adiacenti due diedri consecutivi le cui facce non comuni appartengano allo stesso piano. La somma di due diedri consecutivi è il diedro che ha come spigolo lo spigolo comune e come facce le facce non comuni. La somma di due diedri non consecutivi si ottiene disponendo, mediante una traslazione, uno dei due consecutivo all’altro. Dati due diedri δ e δ′, si dice che δ > δ′ se δ′ è congruente a un diedro avente per facce una faccia di δ e un semipiano interno a δ e avente per origine lo spigolo di δ. La differenza di due diedri è il diedro che aggiunto al minore dei due dà il maggiore. Due diedri la cui somma sia un diedro piatto sono detti diedri supplementari. Un diedro si dice retto, piatto, nullo, acuto, ottuso a seconda che sia rispettivamente retto, piatto, nullo, acuto, ottuso l’angolo piano rappresentato dalla sua sezione normale.