diagramma di biforcazione
diagramma di biforcazione
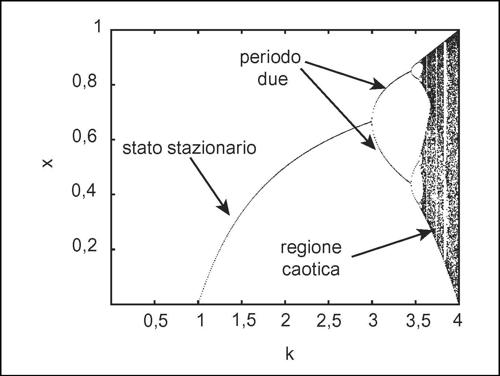
diagramma di biforcazione in teoria dei sistemi dinamici, forma di rappresentazione grafica che illustra i punti critici in cui si manifestano situazioni di → caos o → catastrofe, nelle quali il modello matematico utilizzato non è più adatto a descrivere l’evoluzione di un sistema (→ sistema dinamico). Per esempio, per descrivere la dinamica di crescita di una popolazione si utilizza talvolta l’equazione logistica xn+1 = kxn(1 – xn) che rappresenta, con opportune semplificazioni, il numero xn+1 degli individui della generazione n + 1 in funzione del numero xn degli individui della generazione n. Il valore assunto dal parametro k gioca un ruolo cruciale nell’evoluzione del sistema: al suo crescere da 0 a 4 si passa dall’ordine al caos. In particolare, se k ≤ 3, per qualsiasi valore iniziale x0 si ha un’orbita che finisce in un punto fisso. In particolare, se k < 1 l’orbita finisce in 0, se 1 ≤ k ≤ 3 finisce in un punto fisso diverso da 0. Se invece risulta k > 3, la soluzione salta da un valore a un altro in modo imprevedibile. Per meglio comprendere quel che accade quando il caos comincia a instaurarsi, si ricorre perciò al diagramma di biforcazione che ha in ordinata la popolazione x e in ascissa il parametro k. La regione caotica presenta una struttura autosimile: ciò che avviene su larga scala (un ramo che si biforca in due, e poi in quattro ecc.) lo si ritrova anche su scale minori (→ frattale).
☐ Nella teoria delle equazioni differenziali si parla di grafico di biforcazione in riferimento alla rappresentazione nel piano cartesiano dei punti (λ, u*), dove λ è un parametro presente nell’equazione, u è una soluzione corrispondente al valore del parametro λ e u* una opportuna normalizzazione della soluzione (per esempio il suo valore massimo). Sul grafico di biforcazione possono originarsi ulteriori rami di soluzioni chiamati biforcazioni secondarie.