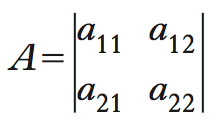determinante
determinante
Funzione che associa a una matrice quadrata A un numero che ne sintetizza alcune proprietà algebriche. Data la matrice quadrata A, di dimensione 2, cioè
dove a11, a12, a21, a22 sono numeri reali o complessi, il d. di A è indicato con det(A) oppure con ∣A∣ ed è definito dalla formula det(A)=a11a22−a12a21. Tale formula è valida soltanto nel caso particolare di una matrice di ordine 2, ma non di ordine n≠2, mentre nel caso in cui la matrice A sia uno scalare, cioè A=a11, il d. coincide con A, det(A)=a11. In generale, il calcolo del d. di una matrice quadrata di dimensione n, come
è un’operazione più complessa quando n≥3. Il numero n è detto ordine del d.; la regola per il calcolo di un d. di ordine n è la seguente: si considerino i prodotti a1h1 a2h2 … anhn, essendo h1, h2, ..., hn i numeri 1, 2, ..., n in una delle loro possibili permutazioni, e a ciascuno di tali prodotti si attribuisca il segno + o il segno − a seconda che la permutazione sia, rispetto a 1, 2, ..., n, di classe pari o dispari: valore del d. è la somma algebrica dei prodotti considerati. Per il calcolo effettivo di un d. di ordine qualunque si può utilizzare il primo teorema di Laplace, secondo il quale il d. di una matrice di ordine n risulta dipendere dai d. di ordine n−1 che si ottengono da A eliminando a turno tutte le righe e una colonna prefissata (o viceversa). Nel calcolo dei d. riescono inoltre utili talune regole e proprietà, tra le quali le seguenti:
• se una matrice quadrata ha due linee (righe o colonne) uguali o proporzionali, ovvero se una linea è tutta nulla, ovvero se una linea è combinazione lineare di più linee parallele, il suo d. è nullo;
• il valore del d. non si altera se a una linea si aggiunge una combinazione lineare qualunque di più linee parallele né se si scambiano di posto due linee parallele intervallate da un numero dispari di linee, mentre tale valore cambia di segno se si scambiano di posto due linee parallele intervallate da un numero pari di linee;
•
se in una matrice gli elementi di una linea sono somme di n addendi, il suo d. è uguale alla somma degli n d. che si ottengono mettendo, al posto di quella linea, una volta la linea formata con i primi addendi, una volta la linea formata con i secondi, e così via, lasciando inalterate le altre linee.
La teoria dei d. permette di rendere compatti sviluppi analitici anche complessi, come per es. quelli richiesti nella risoluzione dei sistemi di equazioni lineari. Di seguito sono riportate alcune proprietà dei d. che riguardano vari tipi di matrici e di operazioni. Meritano particolare attenzione fra queste proprietà: date due matrici quadrate A e B, di dimensione n e a valori nel campo dei numeri reali o complessi, allora det(AB)=det(A)det(B) (teorema di Binet); una matrice quadrata A (di numeri reali o complessi) è invertibile se e solo se det(A)≠0. In tal caso det(A−1)=1/det(A); il d. di una matrice A è uguale a quello della sua trasposta AT:det(A)=det(AT); se λi, i=1,2,…,n sono gli autovalori di una matrice A di dimensione n×n, si ha allora det(A)=λ1λ2… λn; il d. di una matrice diagonale è uguale al prodotto dei termini sulla diagonale principale.