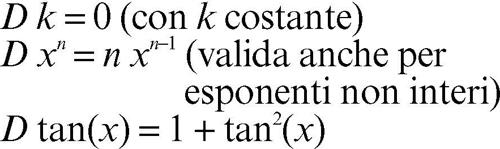derivazione
derivazione
derivazione operazione che a una funzione associa la sua → derivata. Nel caso di funzioni di più variabili, a ciascuna di esse è associato un operatore di derivazione parziale. Lʼoperatore di derivazione per una funzione ƒ(x), indicato con
_lettD_01250_001.jpg>
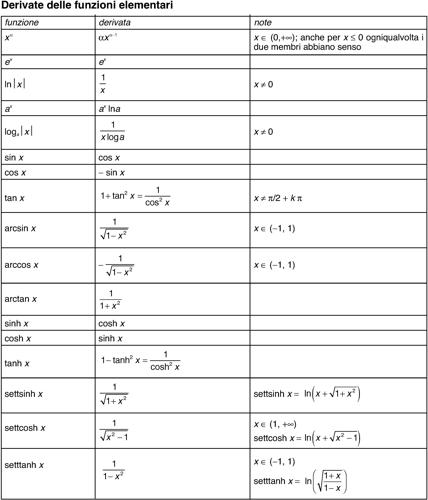
è un operatore lineare tra spazi vettoriali. La derivazione di una funzione di cui sia nota lʼespressione analitica è unʼoperazione implementabile con un algoritmo che utilizza opportune regole, a partire dalle derivate delle funzioni elementari e delle loro inverse. Tali derivate sono:
_lettD_01250_002.jpg>
Nella pratica questo elenco viene completato con altre derivate di facile memorizzazione, per esempio:
(si veda la tavola delle derivate delle funzioni elementari).
Le regole per calcolare la derivata di altre funzioni, a partire da quelle elementari, sono riassunte nei seguenti teoremi, nei quali si suppone che le funzioni siano tutte derivabili e che i denominatori siano diversi da zero:
• linearità della derivazione:
_lettD_01250_004.jpg>
• derivata del prodotto:
_lettD_01250_005.jpg>
• derivata del quoziente:
_lettD_01250_006.jpg
• derivata di una funzione composta:
_lettD_01250_007.jpg>
(detta anche regola della catena, dallʼinglese chain rule)
• derivata della funzione inversa:
_lettD_01250_008.jpg>
Poiché tutte le funzioni elementari si ottengono dalla funzione identità y = x, e dalle funzioni esponenziale e trigonometriche con un numero finito di tali operazioni, basta conoscere le derivate del precedente elenco per poter calcolare le derivate di ogni funzione elementare. Per esempio:
•_lettD_01250_009.jpg>
•_lettD_01250_010.jpg>
•_lettD_01250_011.jpg>
•_lettD_01250_012.jpg>
•_lettD_01250_013.jpg>
•_lettD_01250_014.jpg>
•_lettD_01250_015.jpg>
•_lettD_01250_016.jpg>
Quest’ultimo esempio corrisponde allo schema:
_lettD_01250_017.jpg>
che può essere utilizzato come ulteriore regola di derivazione, pur essendo conseguenza di quelle sopra indicate (si veda la tavola delle regole di derivazione).
