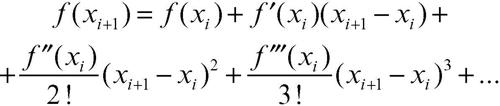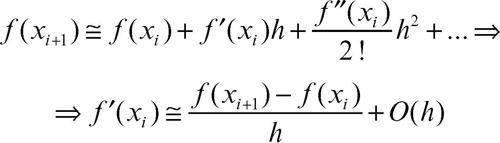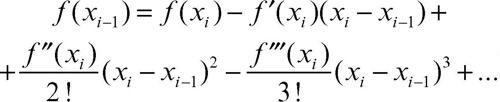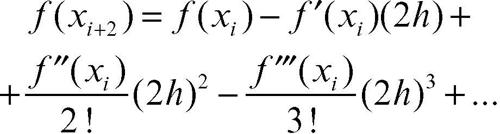derivazione numerica

derivazione numerica

derivazione numerica metodo di calcolo approssimato utilizzato in analisi numerica per la determinazione della derivata, fino a un certo ordine, di una funzione y = ƒ(x) che abbia una espressione analitica di difficile derivazione immediata oppure per la quale sia nota una tabella di valori. I procedimenti di derivazione numerica si basano essenzialmente sulla sostituzione delle derivate con opportuni rapporti incrementali. Il metodo parte dalla definizione di derivata come limite del rapporto incrementale

Non si perde di generalità se si definisce la derivazione numerica come unʼapprossimazione del valore della derivata prima ƒ′′(x) di una funzione y = ƒ(x) calcolata in un punto appartenente al suo dominio: y′ = ƒ′′(x₀). Infatti il calcolo delle derivate successive può essere ricondotto sempre a questo metodo, seppur con qualche piccola modifica. I metodi numerici per il calcolo della derivata si applicano con opportune approssimazioni basate sulla trasformazione di differenze infinitesime in differenze finite (metodo alle differenze finite):

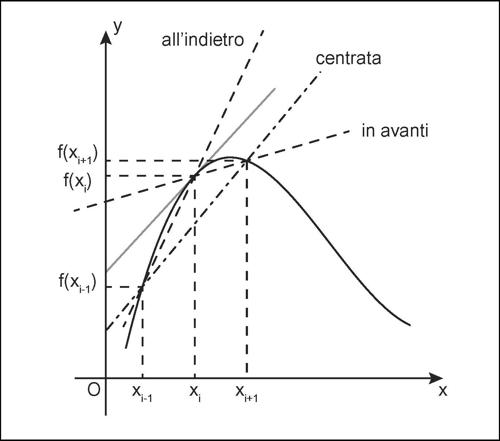
la derivata viene approssimata dalla differenza finita in avanti (forward difference approximation), sostituendo al valore esatto della derivata il valore del coefficiente angolare della retta passante per il punto dato x_i e per il punto successivo x_i+1;

la derivata viene approssimata dalla differenza finita allʼindietro (backward difference approximation), sostituendo al valore esatto della derivata il valore del coefficiente angolare della retta passante per il punto dato x_i e il punto precedente x_i−1;

la derivata viene approssimata dalla differenza finita centrale (central difference approximation) sostituendo al valore esatto della derivata il valore del coefficiente angolare della retta passante per il punto precedente x_i−1 e il punto successivo x_i+1 a quello dato.

Riportando su un grafico i tre metodi di approssimazione, si può evidenziare la differenza tra la pendenza di ciascuna retta, calcolata con i metodi approssimati, e la pendenza della retta tangente in x_i, rappresentante il valore esatto di ƒ′(x_i).

Si può scegliere per semplicità una partizione dell’insieme di definizione della funzione ƒ(x) in modo tale che i valori {x_i} siano equispaziati, ossia x_i+1 – x_i = h, con h costante in tutto lʼintervallo di definizione. Lʼerrore che si commette è tanto minore quanto più piccolo si sceglie h. Infatti è possibile stimare lʼerrore attraverso lo sviluppo in serie di Taylor della funzione ƒ(x) nellʼintorno del punto x_i:

Ponendo x_i+1 − x_i = h:

per h → 0. Lʼerrore in questo metodo è pertanto dellʼordine di h. Analogamente si ricava la formula della differenza finita centrale:

Sottraendo la (b) alla (a) si ottiene:

per h → 0. Si dimostra così che questa formula è più accurata della precedente, avendo un errore che è dellʼordine di O(h²).

Si può sempre usare la formula di Taylor per approssimare le derivate di ordine superiore. Per esempio, per calcolare ƒ″(x) si usa il seguente sviluppo di Taylor, dove x_i+2 = x_i + 2h:

Sottraendo due volte la (a) alla (c) e risolvendo rispetto a ƒ″(x_i) si ottiene la seguente formula:

per h → 0. Si può interpretare il risultato come un metodo di approssimazione in avanti della derivata seconda, avente un errore dellʼordine di O(h). Le approssimazioni del calcolo delle derivate sono usate soprattutto nei metodi numerici per la soluzione delle equazioni differenziali, sia ordinarie che alle derivate parziali.