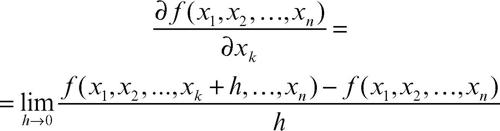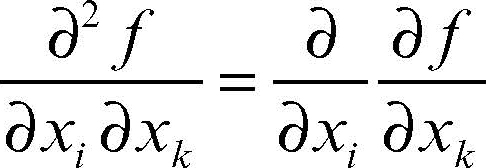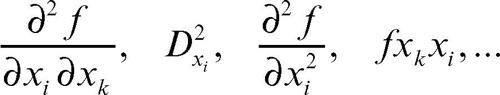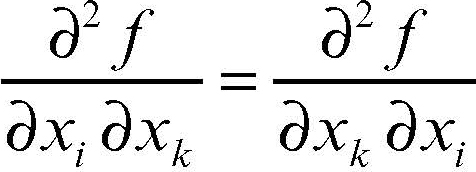derivata parziale
derivata parziale
derivata parziale nozione che generalizza al caso di funzioni di più variabili la usuale definizione di derivata. La derivata parziale di una funzione ƒ(x1, x2, ..., xn) rispetto alla variabile xk è la derivata che si ottiene considerando fissate tutte le altre variabili e calcolando il limite del rapporto incrementale rispetto alla variabile considerata:
Oltre al simbolo indicato, per la derivata parziale rispetto, per esempio, a x si usano anche le notazioni ƒx e Dx ƒ. Le regole di calcolo per le derivate parziali sono identiche a quelle per le derivate in una sola variabile, essendo sufficiente considerare le altre variabili come parametri (→ derivazione). Lʼesistenza delle derivate parziali è condizione necessaria ma non sufficiente per lʼesistenza del differenziale, e anzi non implica neppure la continuità della funzione, come mostra lʼesempio della funzione ƒ(x, y) così definita per casi:
Infatti si ha: ƒx(0, 0) = ƒy(0, 0) = 0 e, quindi, le derivate parziali esistono in (0, 0) ma
e pertanto ƒ non è continua in (0, 0).
Si possono considerare derivate parziali di ordine superiore, ponendo
Le derivate successive rispetto alla stessa variabile si dicono pure, quelle che coinvolgono variabili diverse miste. Esse si indicano in uno dei modi seguenti (nel caso di derivate parziali seconde):
Le derivate seconde, a priori, dovrebbero essere n2 (n per ciascuna delle n derivate prime), ma se sono continue si riducono a n(n + 1)/2 essendo
per il teorema di → Schwarz; questo teorema stabilisce lʼinvertibilità dellʼordine di derivazione e assicura, sotto ipotesi abbastanza generali, la possibilità di eseguire le derivate senza badare allʼordine con cui sono prese in considerazione di volta in volta le variabili, così riducendo il numero di derivate successive effettivamente distinte tra loro. Analogamente avviene per le derivate successive, che, se continue, non dipendono dallʼordine con cui sono valutate.