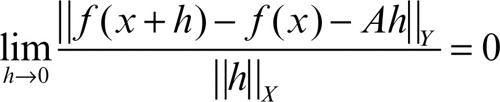Frechet, derivata di

Frechet, derivata di

Fréchet, derivata di generalizzazione a spazi funzionali della nozione di differenziale per funzioni di più variabili. Sia ƒ: X → Y una applicazione tra due spazi di Banach X e Y. Un operatore lineare A: X → Y tale che in un punto x ∈ X risulti

è detto derivata di Fréchet di ƒ in x. Questa nozione è più forte di quella di derivata di Gâteaux. Se X e Y hanno dimensione finita, l’operatore corrisponde alla matrice jacobiana. Per la derivata di Fréchet vale la regola di derivazione delle funzioni composte.