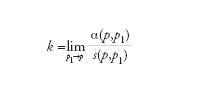curvatura
curvatura
Termine generale che indica una serie di caratteristiche quantitative (in termini di numeri, vettori, tensori) descriventi il grado al quale un determinato oggetto geometrico (una curva, una superficie, uno spazio riemanniano ecc.) si allontana da altri oggetti scelti come riferimenti e considerati come piatti (una linea retta, un piano, uno spazio euclideo). In tutte le sue forme specifiche il concetto di curvatura è definito localmente, per ogni punto fissato dell’oggetto in considerazione e facendo uso esclusivamente di proprietà di insiemi di punti a esso arbitrariamente vicini (intorni). Tali punti devono di norma soddisfare determinate ipotesi di regolarità, che esprimono il fatto che l’oggetto nelle loro vicinanze deve essere sufficientemente ‘liscio’. In generale, se la curvatura si annulla in tutti i punti l’oggetto in questione è identico (localmente, non globalmente) al corrispondente oggetto piatto. Si consideri per es. una curva regolare γ nello spazio euclideo n-dimensionale e siano α(p,p1) e s(p,p1) l’angolo tra le rette tangenti a γ nei punti p e p1 di γ e la lunghezza dell’arco di curva compreso tra p e p1, rispettivamente. Allora il limite
è detto curvatura della curva γ in p. Siano ora Φ una superficie (regolare) nello spazio euclideo tridimensionale, p un punto su di essa, Tπ il piano tangente a Φ in p, n il vettore di lunghezza unitaria ortogonale a Φ in p e infine π il piano su cui giacciono n e un qualunque vettore l su Tπ. L’intersezione di π e Φ definisce una curva γλ e varie nozioni della curvatura di Φ sono definite a partire da quella di γλ per particolari vettori l. Tra queste ricordiamo la curvatura gaussiana o totale, introdotta dal matematico tedesco Carl Friedrich Gauss. A lui si deve il Theorema egregium, nel quale è stabilito che la curvatura di una superficie è determinata dalla sua metrica, ovvero dalla lunghezza delle curve su di essa, e non dalle proprietà dello spazio nel quale la superficie stessa è immersa. Si tratta dunque di una proprietà intrinseca, un’osservazione che opportunamente generalizzata sarà posta da Bernhard Riemann a fondamento della sua nuova geometria.