Vitali, curva di

Vitali, curva di

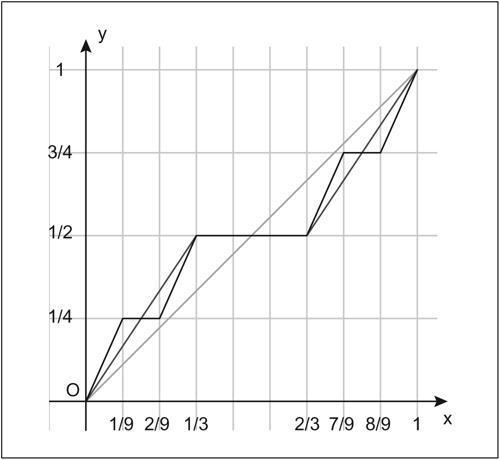
Vitali, curva di rappresentazione di una particolare funzione, detta appunto funzione di → Vitali, derivante dalla definizione dell’insieme ternario di Cantor (→ Cantor, polvere di). Dividendo il segmento in tre parti, nel sottointervallo centrale, corrispondente alla parte di segmento che a ogni iterazione viene tolta, la funzione ha sempre valore costante (la pedata dello scalino), mentre in corrispondenza dei due sottointervalli rimasti, il grafico è dato da due segmenti che uniscono i loro rispettivi estremi. La lunghezza totale di tutte le pedate, per le proprietà dell’insieme di Cantor, è uguale a 1, benché sembrerebbe intuitivamente strettamente minore di 1; la funzione rappresentata dalla curva, inoltre, non è strettamente crescente su alcun sottointervallo di [0, 1].

Insieme alla curva di → Koch e alla curva di → Peano, la curva di Vitali fa parte dell’insieme delle cosiddette → curve patologiche e spesso viene chiamata con il suggestivo nome di curva diabolica o anche scalinata del demonio per le sue proprietà nascoste per nulla intuitive, che possono indurre in errore a una non approfondita analisi delle sue particolari caratteristiche. La curva, dopo poche iterazioni, raggiunge un aspetto tipicamente frattale.