trasformazione, curva di

trasformazione, curva di

Curva che definisce la frontiera delle possibilità produttive attraverso una allocazione efficiente delle risorse a disposizione della società.

Costruzione della curva

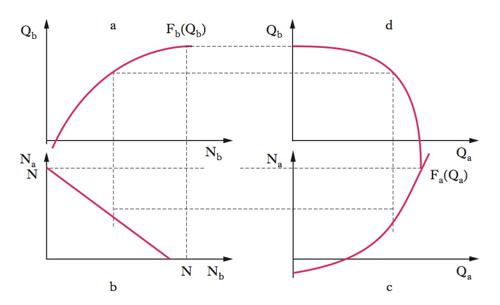
Si consideri un sistema economico semplificato, in cui è presente una sola risorsa, il lavoro (N) disponibile in quantità data, che può essere distribuita nella produzione di due beni (A e B). Per definire le allocazioni efficienti, si dispone dunque dei seguenti dati: due funzioni della produzione (➔ produzione, funzione di), che indicano le quantità massime producibili con i vari impieghi di lavoro (in entrambi i casi si assumono produttività marginali decrescenti, nel senso che l’impiego di dosi successive di lavoro nella produzione di un bene ne accresce il prodotto di una quantità sempre minore); e la quantità complessivamente disponibile della risorsa lavoro. In simboli: Q_a=F_a(N_a); Q_b=F_b(N_b); N_a+N_b=N. Il problema della determinazione delle allocazioni efficienti è chiarito dalla figura, in cui compaiono 4 grafici allineati con gli assi. Nel grafico a è tracciata la funzione di produzione del bene B con N_b in ascissa e Q_b in ordinata; essa è concava per tenere conto della produttività marginale decrescente. Nel grafico c è descritta la funzione di produzione del bene A, con Q_a in ascissa e N_a in ordinata (rispetto al grafico del bene B gli assi sono invertiti e per questo la curva appare convessa). Nel grafico b, con N_b in ascissa e N_a in ordinata, è disegnata una retta le cui intercette sui due assi sono entrambe pari a . e i cui punti hanno la proprietà per cui la somma dell’ascissa e dell’ordinata è costante e pari a N (N_b+N_a=N). Essi identificano tutte le possibili distribuzioni della quantità disponibile di lavoro tra i due beni: l’intercetta orizzontale indica che tutto il lavoro è destinato alla produzione di B; quella verticale che tutto il lavoro è destinato alla produzione di A; gli altri punti indicano le possibilità intermedie. Partendo da uno qualsiasi di essi e riportando le corrispondenti quantità di lavoro nei due grafici a e c, si ottengono le quantità prodotte dei due beni con quella distribuzione del lavoro. Ripetendo l’operazione per ogni punto della retta del grafico b e riportando i risultati (le varie combinazioni di Q_a e Q_b) nel grafico d (con Q_a in ascissa e Q_b in ordinata), si ottiene la curva di t. (denominata anche frontiera delle possibilità produttive). Essa indica, per ogni quantità Q_a, la quantità massima di B producibile utilizzando tutto il lavoro di cui si dispone e  identifica l’insieme delle allocazioni possibili date la risorsa disponibile N e le funzioni di produzione.Tali allocazioni sono appunto quelle sulla curva e quelle racchiuse tra la curva e gli assi (le allocazioni all’esterno sono irraggiungibili, a meno di non disporre di più lavoro). Sulla curva ci sono le allocazioni efficienti, nelle quali non è possibile aumentare la produzione di un bene senza ridurre quella dell’altro. Le altre sono allocazioni inefficienti, dove è sempre possibile incrementare  Q_a senza far scendere Q_b e viceversa.

Punto di frontiera e costo-opportunità

Se l’allocazione della risorsa è efficiente (cioè usata interamente e senza sprechi), il sistema economico si trova in un punto sulla frontiera. Questa consente di calcolare la quantità di un bene a cui si deve rinunciare se si vuole accrescere la produzione dell’altro, di determinarne cioè il costo-opportunità (➔ costo-opportunità, teoria del) in termini dell’altro; se invece l’allocazione di partenza è inefficiente, il costo-opportunità è zero. Si noti infine che, poiché la frontiera è concava (a causa delle produttività marginali decrescenti), il costo-opportunità di un prodotto cresce costantemente: si deve rinunciare a una quantità sempre maggiore di uno per ottenere un’unità addizionale dell’altro.