Sierpinski, curva di

Sierpinski, curva di

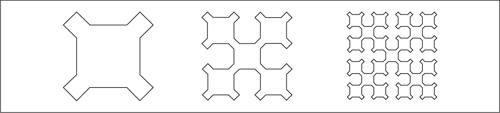
Sierpiński, curva di denominazione di alcune curve frattali piane, continue, definite per ricorrenza, che, al tendere all’infinito del numero dei passi, riempiono il quadrato unitario. Proprio in quanto riempie una superficie, una curva di Sierpiński ha dimensione di Hausdorff uguale a 2 (→ dimensione frattale); essa si ottiene come limite S di una successione di curve chiuse {S_n} che rimangono all’interno di un quadrato, ma sono costituite da un numero crescente di moduli che si riproducono in dimensioni ridotte. Le lunghezze delle curve S_n crescono esponenzialmente con n e pertanto S, pur racchiudendo una superficie di area finita, non ha lunghezza finita. La curva di Sierpiński trova applicazione nel problema del → commesso viaggiatore, consistente nell’individuare il percorso più breve che passa per tutti i punti di un dato insieme: un algoritmo euristico per la sua soluzione segue un percorso di visita che ricalca la generazione dei moduli “quadrati” che compaiono in tale curva (si veda anche → frattale).