Crittografia
Crittografia
La crittografia è la disciplina che studia le tecniche per trasformare un messaggio, detto testo in chiaro, in un altro messaggio, detto testo cifrato, che risulta incomprensibile a chiunque non conosca tutti i dettagli della tecnica usata per la trasformazione. Solo il legittimo destinatario del messaggio è in grado di effettuare l’operazione inversa e di ottenere così dal testo cifrato il testo in chiaro originale.
La trasformazione del testo in chiaro in testo cifrato è detta cifratura, mentre la ricostruzione del testo in chiaro a partire dal testo cifrato è detta decifratura. L’insieme delle operazioni che devono essere effettuate durante la cifratura e la corrispondente decifratura prende il nome di codice crittografico, o cifrario, o anche semplicemente codice.
Una disciplina strettamente collegata alla crittografia è la criptoanalisi, il cui scopo è scoprire modi per decifrare i messaggi pur non conoscendo il metodo utilizzato per la cifratura, ossia per ‘attaccare’ e, possibilmente, ‘rompere’ il codice. La sua funzione è importantissima, perché gli studi compiuti dai criptoanalisti possono portare alla lu-ce debolezze che sono sfuggite agli stessi progettisti di un cifrario. Le difficoltà che il criptoanalista deve affrontare variano a seconda delle informazioni di cui dispone: la situazione più difficile è quella in cui egli ha a disposizione il solo testo cifrato e ignora quale tipo di codice sia stato utilizzato per produrlo.
La crittografia è nata inizialmente per garantire la segretezza delle comunicazioni in campo militare. Un esempio antico di codice crittografico è il codice di Cesare generalizzato, utilizzato da Giulio Cesare per le comunicazioni con i suoi generali. Esso si basa sulla sostituzione di ogni lettera del testo in chiaro con quella che si trova, nell’ordinamento alfabetico, k posizioni dopo, considerando l’alfabeto chiuso circolarmente (da A a Z). Il valore di k può essere variato di volta in volta, a ogni operazione di cifratura, e prende il nome di chiave di cifratura. Ovviamente, la stessa chiave deve essere utilizzata nella cifratura e nella corrispondente decifratura di un messaggio. Il lavoro per il criptoanalista è molto facile per ottenere il testo in chiaro; egli dovrà provare semplicemente a usare tutti i possibili valori della chiave che, per esempio, nel caso dell’alfabeto italiano sono 21. Questo tipo di attacco è detto attacco di forza bruta e, in linea di principio, può essere utilizzato con qualsiasi codice.
Un considerevole miglioramento è costituito dal cosiddetto cifrario monoalfabetico: esso sostituisce ogni lettera del testo in chiaro con un’altra, ma in modo meno regolare. Infatti, qualsiasi lettera può essere sostituita da qualunque altra, purché in un’operazione di cifratura ciascuna lettera, ogni volta che appare, sia sempre sostituita dalla stessa. La chiave di cifratura, in questo caso, è molto più articolata che nel caso precedente, perché è costituita da una qualunque permutazione delle lettere dell’alfabeto. In questo caso un attacco di forza bruta è molto più oneroso, perché ci sono 21! (ca. 5×1019) possibili permutazioni.
Circa quattro secoli or sono fu introdotto il metodo del cifrario polialfabetico (noto anche come cifrario di Vigenère), basato sull’uso di più cifrari monoalfabetici, applicati uno dopo l’altro alle successive lettere del testo in chiaro, in una singola operazione di cifratura e nella corrispondente decifratura. L’innovazione principale è data dal fatto che una stessa lettera, la quale appare in differenti posizioni del testo in chiaro, può essere sostituita di volta in volta da lettere diverse.
Crittografia a chiave segreta
In questo tipo di crittografia, il mittente e il destinatario (che chiameremo rispettivamente A e B) si accordano, per esempio incontrandosi di persona e lontano da occhi indiscreti, su una chiave k che verrà usata sia in fase di cifratura sia di decifratura. Il metodo di cifratura è una funzione, E, che accetta in ingresso il testo in chiaro P e la chiave k, producendo il testo cifrato C.
Il metodo di decifratura è un’altra funzione D (ovviamente collegata alla prima), che accetta in ingresso il testo cifrato C, la stessa chiave k utilizzata per la cifratura e restituisce il testo in chiaro originale.
Tutti i moderni cifrari a chiave segreta condividono alcune caratteristiche di fondo. Essi operano su un blocco di bit alla volta (cifratura a blocchi) e sono costituiti da un certo numero di stadi, ciascuno dei quali riceve in ingresso i valori prodotti in uscita dallo stadio precedente e in uscita fornisce i valori allo stadio successivo. In molti di tali stadi la trasformazione operata sui bit è basata sull’uso di raffinati meccanismi di calcolo, detti reti di sostituzione e permutazione (substitution-permutation networks) che, ricevendo in ingresso i bit da elaborare e la chiave di cifratura (o un sottoinsieme dei suoi bit) producono i bit in uscita. È soprattutto la struttura delle reti di sostituzione e permutazione (spesso chiamate S-box) che costituisce il cuore del progetto di un codice e ne caratterizza la robustezza rispetto a due moderni tipi di criptoanalisi: la criptoanalisi differenziale e la criptoanalisi lineare, che cercano di ricostruire la struttura del codice indagando matematicamente le regolarità e correlazioni che si dovessero riscontrare nel testo cifrato.
L’algoritmo DES
L’algoritmo più diffuso in questa categoria è il DES (Data encryption standard), inventato dall’IBM e adottato nel 1977 dal governo degli Stati Uniti per la protezione di informazioni non classificate. Il testo in chiaro è codificato in blocchi di 64 bit, che producono ciascuno 64 bit di testo cifrato. Il DES è stato al centro di controversie sin dal giorno in cui è nato. Il progetto originario dell’IBM prevedeva l’uso di una chiave da 128 bit, ma il governo degli Stati Uniti richiese che la dimensione della chiave fosse ridotta a soli 56 bit. Tale richiesta era motivata, secondo molti studiosi del settore, dall’esigenza di preservare la possibilità di rompere (con opportune, potenti macchine) il codice. Inoltre, dato che i criteri di progetto degli S-box non furono mai divulgati, molti ricercatori sospettarono che essi contenessero delle regolarità nascoste per consentire la decifratura dei messaggi da parte di enti governativi americani. Questa ipotesi non fu mai né provata né dimostrata falsa, anche se il tempo ormai trascorso fa ritenere che essa non fosse vera: infatti, l’intenso studio effettuato per anni dalla comunità scientifica internazionale sulle caratteristiche degli S-box non ha portato alla luce alcuna di tali presunte regolarità. Attualmente, comunque, il DES non è più considerato sicuro per due ragioni. In primo luogo, uno spazio di ricerca di 256 chiavi è considerato ormai troppo modesto per proteggere da attacchi di forza bruta compiuti con potenti elaboratori multiprocessore o con sistemi costituiti da un grande numero di elaboratori cooperanti e collegati fra loro. La seconda ragione di debolezza del DES, di interesse più teorico che pratico, risiede nel fatto che, come è stato dimostrato con tecniche di criptoanalisi lineare e differenziale, lo spazio di ricerca per gli attacchi di forza bruta può essere ridotto a sole 243 possibilità.
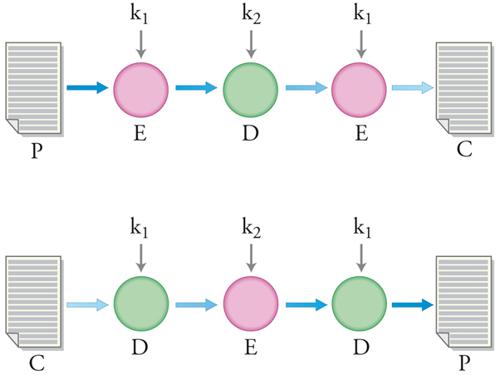
Una variante del DES, il DES triplo, è però ancora considerata sicura, in quanto non si conosce alcun modo di romperla se non con un attacco di forza bruta. Il meccanismo della cifratura DES tripla è semplice: a una prima fase di cifratura DES, effettuata con una chiave k1, segue una fase di decifratura DES effettuata con una chiave k2, quindi un’ulteriore fase di cifratura DES di nuovo mediante la chiave k1. La decifratura DES tripla compie i passi inversi. Questo schema, ponendo k1=k2, garantisce la compatibilità all’indietro col normale DES (fig. 2).
Effettivamente il DES triplo costituisce un codice per il quale l’approccio della forza bruta richiede 2112 tentativi: anche con un miliardo di chips che effettuano un miliardo di operazioni al secondo, ci vorrebbero 100 milioni di anni per un attacco di forza bruta.
L’algoritmo AES
Il 2 gennaio 1997 l’ente americano NIST (National Institute of Standards and Technology) iniziò il procedimento per designare il successore del DES, denominato AES (Advanced encryption standard). Tale procedimento si sviluppò attraverso varie fasi, tutte gestite all’insegna della massima diffusione internazionale e della circolazione delle idee e delle proposte, e si concluse il 4 dicembre 2001 con la scelta del cifrario Rijndael, il cui nome deriva da quello dei due autori, i belgi Joan Daemen e Vincent Rijmen.
AES (ossia il cifrario Rijndael) effettua la cifratura su blocchi di 128 bit, e può utilizzare chiavi di 128, 192 oppure 256 bit. Il numero di stadi dipende dalla lunghezza della chiave usata: si impiegano 10 stadi con chiavi da 128 bit, 12 stadi con chiavi da 192 bit e 14 stadi con chiavi da 256 bit.
Gli S-box sono stati progettati con grande attenzione e sono stati oggetto di approfondite indagini da parte della comunità scientifica internazionale. Non sono noti risultati di criptoanalisi che indeboliscano AES, e la lunghezza delle chiavi utilizzabili (soprattutto nel caso del valore 256) rende privo di speranze un attacco di forza bruta.
Crittografia a chiave pubblica
Nella seconda metà degli anni Settanta, un tipo di crittografia radicalmente nuovo, detto a chiave pubblica (o asimmetrica), fu introdotto dai ricercatori Whitfield Diffie e Martin E. Hellman, della Stanford University. Questo nuovo tipo di crittografia è basato sul fatto che per ogni utente esistono due chiavi, legate l’una all’altra: una è la chiave privata, nota solo al proprietario; l’altra è la chiave pubblica, nota a tutti. Ciò che viene cifrato con una delle due chiavi può essere decifrato soltanto con l’altra. Naturalmente, deve essere praticamente impossibile, ossia estremamente oneroso dal punto di vista computazionale, derivare la chiave privata conoscendo quella pubblica.
Se ciò che si desidera è la segretezza, si opera in questo modo: il messaggio viene cifrato dal mittente A con la chiave pubblica del destinatario B (che è nota a tutti); B decifra il messaggio con la propria chiave privata (che è nota solo a lui).
La crittografia a chiave pubblica fornisce anche un meccanismo per garantire l’autenticazione del mittente (cioè la garanzia che il documento ricevuto provenga veramente dall’autore e non da qualcun altro) e l’integrità del messaggio (cioè la garanzia che il messaggio non sia stato alterato). In questo caso si opera alla rovescia: A cifra il messaggio con la propria chiave privata, e B lo decifra con la chiave pubblica di A. In questo caso non c’è segretezza, dato che chiunque può decifrare il messaggio, ma nessuno se non A avrebbe potuto produrlo, e inoltre nessuno può averlo alterato (altrimenti la decifratura non produrrebbe un documento comprensibile).
L’algoritmo RSA
L’algoritmo a chiave pubblica più noto e di gran lunga più utilizzato attualmente è l’algoritmo RSA, dalle iniziali degli autori Ronald L. Rivest, Adi Shamir e Leonard M. Adleman, sviluppato nel 1978. La sua sicurezza si basa sull’enorme difficoltà di trovare i fattori primi (ossia di fattorizzare) di un grande numero: si stima che serva un miliardo di anni di tempo-macchina per fattorizzare un numero di 200 cifre, e 1025 anni per un numero di 500 cifre.
Nel 1994, dopo che gli autori avevano pubblicato sulla rivista “Scientific American” una sfida, l’RSA fu rotto. Il procedimento si riferiva a una chiave di 129 cifre, e furono impiegati 1600 elaboratori su Internet per 8 mesi, corrispondenti a un totale di 5000 anni di tempo-calcolo di un singolo elaboratore capace di milioni di istruzioni al secondo. D’altronde, poiché RSA lavora con i numeri, la dimensione della chiave è variabile e può essere aumentata a piacere, per controbilanciare gli effetti derivanti dal miglioramento delle prestazioni degli elaboratori.
C’è però una considerazione interessante da fare in merito alla sicurezza di RSA: la sua robustezza deriva, come già detto, dall’enorme difficoltà di fattorizzare un grande numero primo. Ebbene, per il problema della fattorizzazione non esiste, allo stato attuale delle conoscenze scientifiche, né una soluzione efficiente (cioè praticabile) né la dimostrazione che non sia possibile trovarla in futuro. Nel momento in cui tale soluzione dovesse venire alla luce, in pratica l’RSA cesserebbe istantaneamente di essere un cifrario utilizzabile, perché non sarebbe più sicuro.
Funzioni digest e firme digitali
Come si è detto, la crittografia a chiave pubblica può essere usata per autenticare l’origine di un messaggio e per garantirne l’integrità, ossia di fatto per firmare un messaggio. Tuttavia, a causa dell’elevato costo computazionale, questo approccio sembra inadatto: cifrare tutto il messaggio solo per firmarlo è poco efficiente. Inoltre, è scomodo rendere l’intero documento illeggibile ove solo una firma sia richiesta. Ambedue i problemi si possono risolvere con una tecnica diversa e più efficiente.
La tecnica in questione si basa sull’uso delle cosiddette funzioni riassunto (funzioni digest), che vengono applicate al messaggio e producono un valore numerico che viene detto, appunto, riassunto del messaggio. Tale valore numerico è rappresentabile tipicamente con una quantità di bit che varia tra 128 e 256, indipendentemente dalla lunghezza del messaggio originario.
Gli algoritmi più diffusi per la generazione del riassunto sono MD5 (Message digest 5, il quinto di una serie) e SHA (Secure hash algorithm). Il primo produce riassunti di 128 bit, il secondo di 160 bit.
Protocolli crittografici
Un protocollo crittografico ha lo scopo di specificare le regole che le parti debbono seguire per assicurarsi una conversazione conforme ai requisiti desiderati. Un protocollo crittografico in generale non specifica quali algoritmi vadano usati nei vari passi, ma piuttosto le tecniche da adottare (per es., crittografia a chiave pubblica e/o privata, riassunti dei messaggi e via dicendo), la successione dei passaggi da seguire, e quale tecnica necessiti di essere impiegata a ogni passo.
Esistono vari protocolli crittografici, che si differenziano per il contesto iniziale (per es., i due partecipanti possono avere o meno una chiave segreta in comune; possono conoscere o meno le rispettive chiavi pubbliche) e gli scopi da raggiungere (autenticazione, segretezza, o entrambe le cose). Verranno ora descritti brevemente alcuni protocolli molto utilizzati in un contesto come quello della rete Internet e in particolare del world wide web, dove è possibile aver bisogno di autenticazione e segretezza nel dialogo con entità mai conosciute prima e per di più i canali sono insicuri e soggetti all’attacco da parte di intrusi.
Firma digitale
Un primo e semplice protocollo crittografico è il seguente, volto a garantire l’integrità del messaggio: A calcola il riassunto del messaggio da spedire e cifra tale riassunto con la propria chiave privata; invia quindi il messaggio in chiaro corredato del riassunto cifrato. Quando B riceve il tutto, decifra il riassunto con la chiave pubblica di A, ricalcola nuovamente il riassunto del messaggio e lo confronta con quello decifrato: se i due sono identici accetta il messaggio, altrimenti lo rifiuta. Il riassunto cifrato in questo modo è chiamato firma digitale, perché assicura sia l’integrità del messaggio sia l’autenticità del mittente, proprio come una firma apposta (in originale) in calce a un documento cartaceo.
Chiave segreta di sessione
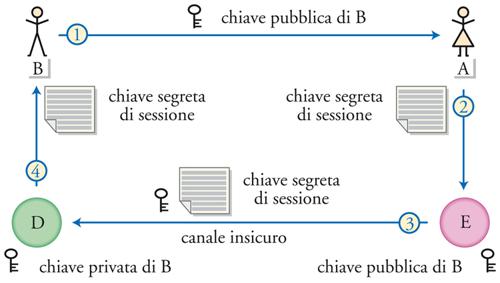
Un altro problema da affrontare e risolvere mediante un protocollo crittografico è legato al fatto che nel corso della comunicazione da portare avanti in modo sicuro è consigliabile utilizzare la crittografia a chiave segreta, in quanto essa è computazionalmente meno onerosa di quella a chiave pubblica. Tuttavia, in un contesto distribuito come il web, è impensabile che ogni potenziale coppia di utenti disponga di una chiave segreta. Dunque, occorre trovare un protocollo per concordare, all’inizio della sessione, la chiave segreta da usare durante il resto della sessione, detta per questo chiave segreta di sessione.
Esso funziona come segue: (a) B invia la sua chiave pubblica ad A; (b) A genera una chiave segreta (diversa da tutte quelle precedentemente generate), la cifra con la chiave pubblica di B e la invia a quest’ultimo; (c) B riceve la chiave segreta (cifrata) e la decifra con la propria chiave privata; (d) A e B a questo punto condividono la chiave segreta di sessione per mezzo della quale possono comunicare in tutta sicurezza (fig. 3).
Certificati digitali
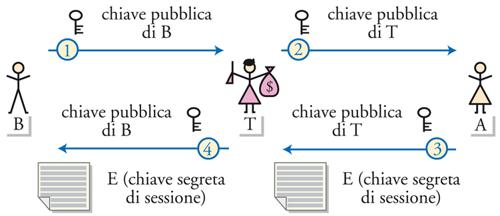
In entrambi i protocolli precedenti vi è però un problema di fondo molto serio. Infatti, un intruso T può riuscire a fare in modo che A riceva, al posto della chiave pubblica di B, quella di T, e quindi a interporsi nella successiva comunicazione e a decifrare tutto (man in the middle attack) (fig. 4).
Per risolvere questo problema s’introduce una nuova entità, l’autorità di certificazione (Certificate authority). Si tratta di un ente, di norma governativo o comunque dotato di credibilità internazionale, che è in grado di creare, per ciascuno dei suoi clienti registrati, un certificato digitale, ossia un documento che contiene: (a) le informazioni pertinenti relative al cliente (identità, autorizzazioni varie, altre informazioni a seconda dei tipi di certificati); (b) la chiave pubblica del cliente; (c) una data di scadenza del certificato stesso; (d) il riassunto cifrato con la chiave privata del centro, ossia la firma digitale del centro.
I protocolli visti vengono quindi modificati nel senso che la chiave pubblica del mittente viene consegnata al destinatario sotto forma di un certificato rilasciato al mittente da un’autorità di certificazione. In questo modo il destinatario, dopo aver decifrato con successo la firma digitale apposta dall’autorità di certificazione, ha la garanzia che la chiave pubblica contenuta nel certificato è proprio quella del legittimo mittente e non quella di un intruso.
Il protocollo SSL
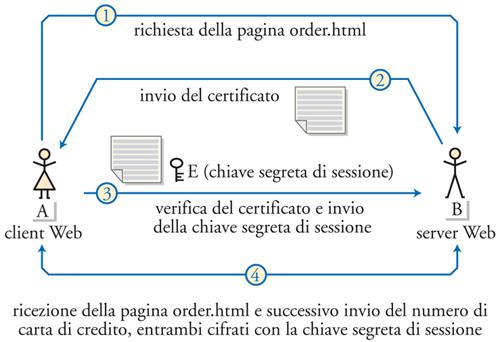
I certificati prodotti da un’autorità di certificazione possono essere conservati dove si desidera. Per esempio, B può mantenere una copia del proprio certificato, e A può chiederlo direttamente a B anziché all’autorità di certificazione. Questo è precisamente quanto avviene nel web quando, per esempio, si invia il proprio numero di carta di credito per effettuare un acquisto via Internet. In questo caso entra in gioco il protocollo SSL (Secure sockets layer, fig. 5), sviluppato in origine da Netscape Communications Corporation, il quale prevede che venga negoziata una chiave segreta di sessione fra il cliente e il fornitore del servizio, previa ricezione da parte del cliente del certificato digitale del fornitore del servizio. Mediante tale chiave segreta il numero di carta di credito del cliente viene quindi cifrato prima di essere inviato sulla rete.
Problemi aperti e conclusioni
Il settore della crittografia è in continua evoluzione. Innanzitutto va sottolineato il fatto che esso pone problemi alquanto delicati, in quanto il suo impatto sociale è decisamente considerevole: da un lato c’è la legittima esigenza dei privati cittadini e delle organizzazioni che operano nella piena legalità di garantirsi la necessaria privacy nelle comunicazioni riservate; dall’altro c’è l’altrettanta legittima aspirazione dei governi a impedire che organizzazioni di stampo criminale possano disporre di strumenti che consentano loro di portare avanti azioni illegali scambiandosi informazioni che non possono essere intercettate. Di conseguenza, è da anni in corso un acceso dibattito, che non pare avviarsi a conclusione, su quale sia il giusto compromesso fra queste due esigenze.
Un altro aspetto caratteristico di questo settore è la continua gara fra crittografia e criptoanalisi: per ogni nuova proposta della crittografia, la criptoanalisi si ingegna a trovare possibili punti di debolezza, che, qualora scoperti, vengono a loro volta presi in considerazione dalla crittografia per progettare nuove tecniche che ne siano immuni.
Un problema interessante, oggetto di numerosi studi in questi ultimi anni, è la gestione di chiavi crittografiche per gruppi di utenti che vogliono comunicare fra loro in maniera sicura, per esempio in sistemi di videoconferenza o sistemi di supporto al lavoro di gruppo. In genere questi gruppi sono variabili nel tempo (per es., nuovi membri del gruppo si aggiungono e altri lo abbandonano), quindi sorge da un lato la necessità di consegnare la chiave a ogni nuovo membro del gruppo, e dall’altro è indispensabile modificare la chiave di gruppo ogni volta che un membro lo abbandona, per evitare che egli possa continuare a decifrare le informazioni una volta che non fa più parte del gruppo.
Va detto infine che un cifrario incondizionatamente sicuro, cioè che non possa in alcun modo essere violato, in pratica non esiste. Oggi viene considerato adeguato un cifrario che sia computazionalmente sicuro, ossia un cifrario che soddisfi le seguenti due proprietà: il costo da affrontare, in termini di risorse impiegate, per rompere un codice deve superare il valore delle informazioni cifrate mediante tale codice; il tempo di calcolo necessario per rompere un codice deve essere superiore al tempo di vita utile delle informazioni cifrate mediante tale codice.
Bibliografia
Akl 1983; Akl, Selim G., Digital signatures: a tutorial survey, “Computer”, 16, 1983, pp. 15-24.
Biham, Shamir 1993: Biham, Eli - Shamir, Adi, Differential cryptanalysis of the Data Encryption Standard, New York, Springer, 1993.
Challal, Seba 2005: Challal, Yacine - Seba, Hamida, Group key management protocols: a novel taxonomy, “International journal of information technology”, 2, 2005, pp. 105-118.
Daemen, Rijmen 2000: Daemen, Joan - Rijmen, Vincent, The block cipher Rijndael, in: Smart card research and applications. Third international conference - CARDIS ’98, Louvain-la-Neuve, Belgium, september 14-16, 1998. Proceedings, edited by Jean-Jacques Quisquater, Bruce Schneier, Berlin-London, Springer, 2000, pp. 288-296.
Diffie 1988: Diffie, Withfield, The first ten years in public-key cryptography, “Proceedings of the IEEE”, 76, 1988, pp. 560-577.
Electronic Privacy Information Center 2000: Crypto-graphy and liberty 2000. An international survey of encryption policy (http://www2.epic.org/reports/crypto2000/).
IETF (Internet Engineering Task Force) 1995: The Secure Sockets Layer Protocol (SSL) (http://www.ietf.org/proceedings/95apr/sec/cat.elgamal.slides.html).
Kahn 1996: Kahn, David, The codebreakers: the story of secret writing, 2. ed., New York, Scribner’s, 1996 (trad. it.: La guerra dei codici: la storia dei codici segreti, Milano, Mondadori, 1969).
Kaliski, Robshaw 1995: Kaliski, Burt S. jr - Robshaw, Matt J.B., The secure use of RSA, “CryptoBytes”, 1, 1995, pp.7-13.
Konheim 1981: Konheim, Alan, Cryptography: a primer, New York, Wiley, 1981.
Matsui 1994: Matsui, Mitsuru, Linear cryptanalysis for DES cipher, in: Advances in cryptology. EUROCRYPT ’93. Workshop on the theory and application of cryptographic techniques, Lofthus, Norway, may 1993. Proceedings, edited by Tor Helleseth, Berlin-New York, Springer, 1994, pp. 386-397.
Menezes 1997: Menezes, Alfred J. - van Oorschot, Paul C. -Vanstone, Scott, Handbook of applied cryptography, Boca Raton (Fl.), CRC Press, 1997.
Nechvatal 1992: Nechvatal, James, Public key cryptography, in: Contemporary cryptology: the science of information integrity, edited by Gustavus J. Simmons, New York, IEEE Press, 1992, pp. 179-195.
Nechvatal 2000: Nechvatal, James e altri, Report on the development of the Advanced Encryption Standard (AES), Washington, National Institute of Standards and Technology, 2000.
NIST (National Institute of Standards and Techno-logy) 1995: Secure Hash Standard (SHA-1), Federal Information Processing Standards Publication 180-1, Washington, NIST, 1995.
NIST (National Institute of Standards and Techno-logy) 2001: Advanced Encryption Standard (AES), Federal Information Processing Standards Publication 197, Washington, NIST, 2001.
Rivest 1978: Rivest, Ronald - Shamir, Adi - Adleman, Leonard, A method for obtaining digital signatures and public key cryptosystems, “Communications of the ACM”, 21, 1978, pp. 120-126.
Rivest 1992: The MD5 Message-Digest algorithm, Internet Requests for Comments (RFC) n. 1321, april 1992, edited by Ronald Rivest (http://www.faqs.org/rfcs/rfc1321.html).
Schneier 1996: Schneier, Bruce, Applied cryptography: protocols, algorithms and source code in C, New York, Wiley, 1996.
Simmons 1992: Contemporary cryptology: the science of information integrity, edited by Gustavus J. Simmons, New York, IEEE Press, 1992.
Stinson 2002: Stinson, Douglas, Cryptography: theory and practice, 2. ed., Boca Raton, (Fl.), CRC Press, 2002.
Wiener 1996: Wiener, Michael J., Efficient DES key search, in: Practical cryptography for data internetworks, edited by William Stallings, Los Alamitos (Cal.), IEEE Computer Society Press, 1996, pp. 31-79.