costruzione con riga e compasso

costruzione con riga e compasso

costruzione con riga e compasso procedura tipica della geometria euclidea che consiste nel tracciare segmenti e angoli utilizzando una riga e un compasso non graduati. Riga e compasso, così intesi, sono strumenti ideali che permettono di tracciare qualsiasi segmento e di prolungarlo indefinitamente in ciascuno dei due versi, nonché di tracciare archi di qualsiasi raggio. La riga non è utilizzabile per effettuare misurazioni. Le operazioni grafiche di base della geometria con riga e compasso sono:

• congiungere due punti o prolungare un segmento;

• tracciare una circonferenza di dato centro e passante per un dato punto;

• determinare l’eventuale punto di intersezione di due rette;

• determinare gli eventuali punti di intersezione di una circonferenza con una retta;

• determinare gli eventuali punti di intersezione di due circonferenze.

A partire da tali operazioni grafiche elementari si definiscono costruzioni più complesse che la geometria euclidea utilizza sia per la risoluzione di problemi sia per la dimostrazione di teoremi. I problemi con riga e compasso furono al centro della geometria di Euclide e, in generale, della geometria degli antichi greci, che era insieme costruttiva e ideale: costruttiva, perché l’esistenza di una figura o di una configurazione doveva essere garantita dalla sua costruibilità attraverso i due strumenti privilegiati; ideale, perché indifferente agli errori e alle approssimazioni degli strumenti reali o alle loro dimensioni. Per molti dei problemi posti, anche di semplice formulazione, quali per esempio la trisezione dell’angolo (→ angolo, trisezione dell’) o la quadratura del cerchio (→ quadratura), si cercò a lungo la soluzione, ma soltanto nel xix secolo, grazie soprattutto a E. Galois, si giunse a comprendere che essi non erano risolubili con riga e compasso e si definirono teoricamente le condizioni generali di non risolubilità. Tutti i problemi di costruzione con riga e compasso sono infatti traducibili, definendo nel piano un opportuno sistema di riferimento, in termini algebrici e conducono alla risoluzione di una equazione. Le operazioni grafiche consentite da riga e compasso, tradotte algebricamente, conducono alle quattro usuali operazioni e all’estrazione di radice quadrata (eventualmente ripetuta): pertanto, un problema di costruzione con riga e compasso che una volta riformulato in termini algebrici dà luogo a una equazione polinomiale il cui grado non è una potenza di 2 non è risolubile.

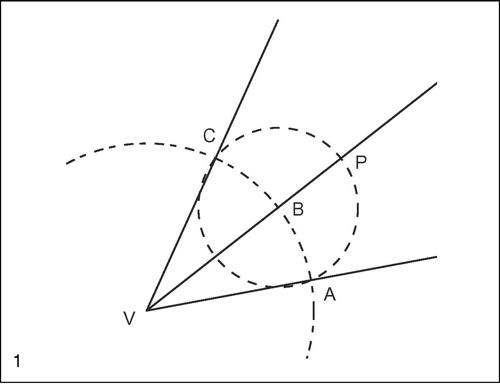
Duplicazione di un angolo

Dato l’angolo

con centro in V si tracci una circonferenza di raggio arbitrario e siano A e B le sue intersezioni con i lati dell’angolo. Si tracci la circonferenza di centro B, passante per A, la si intersechi con la precedente circonferenza e si indichi con C l’ulteriore intersezione. Tracciata la semiretta VC, si delimita l’angolo

doppio dell’angolo

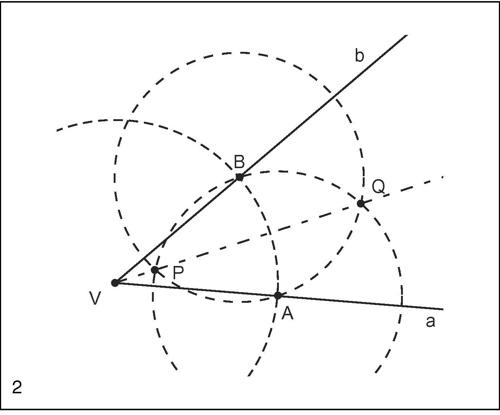
Bisezione di un angolo

Equivale alla costruzione della bisettrice di un angolo. Dato l’angolo α, di vertice V e lati a e b, si tracci una circonferenza con centro in V e si indichino con A e B le sue intersezioni con i lati dell’angolo. Si traccino successivamente le circonferenze di centro A passante per B e la circonferenza di centro B passante per A, e si indichino con P e Q le loro intersezioni. La semiretta VP (che passa anche per Q) è la bisettrice dell’angolo α, dunque lo divide in due angoli uguali. La suddivisione di un angolo in n parti uguali, con n > 2, non è in generale realizzabile con riga e compasso.

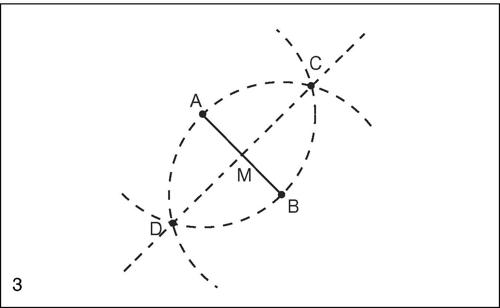
Costruzione di un poligono regolare di n lati

Problema equivalente a quello della suddivisione della circonferenza in n parti uguali (ciclotomia). Il problema era stato posto nell’antica Grecia e già per n = 7 non se ne conosceva la soluzione. Solo nel xix secolo C.F. Gauss ne diede una soluzione in generale, dimostrando che la ciclotomia con riga e compasso è possibile se e solo se n è un numero del tipo 2^m · p₁ · … · p_s, dove p₁, …, p_s equivalgono a 1 oppure sono numeri di Fermat primi e distinti tra loro. La costruzione del triangolo equilatero di lato AB permette di costruire tutti i poligoni regolari con 2ⁿ · 3 lati. Si traccino le circonferenze aventi centro in un estremo di AB e passanti per l’altro estremo, e si indichino con C e D i punti in cui le due circonferenze si intersecano. La costruzione del triangolo equilatero di lato AB risolve anche il problema della determinazione dell’asse di un segmento e del punto medio di un segmento.

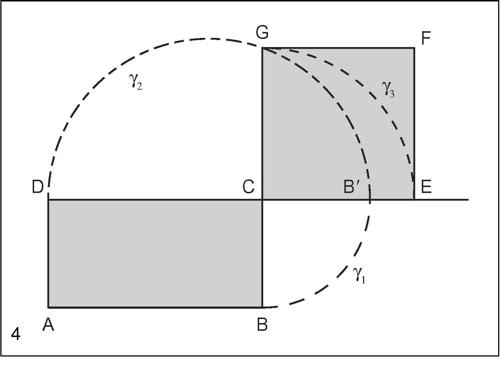
Costruzione del quadrato equivalente a un dato rettangolo

Dato il rettangolo ABCD, sia B′ l’intersezione del prolungamento del lato CD con la circonferenza γ₁ di centro C e raggio CB, e sia G l’intersezione del prolungamento del lato BC con la circonferenza γ₂ di diametro DB′. Il segmento CG è il lato del quadrato equivalente al rettangolo ABCD. Si completa la costruzione tracciando la circonferenza γ₃ di centro C e raggio CG e le rette perpendicolari per E e G, rispettivamente alle rette BC e CD.

Costruzione della perpendicolare da un punto esterno a una retta

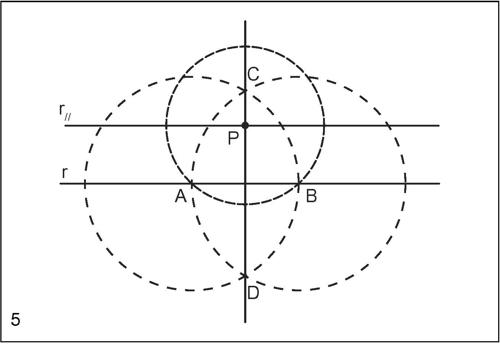
Dati una retta r e un punto P che non le appartiene, si tracci una circonferenza con centro in P che interseca la retta r nel punti A e B. L’asse di AB è la retta r_⊥ perpendicolare per P alla retta data r.

Costruzione della parallela per un punto a una retta

La parallela per P alla retta r si ottiene costruendo la perpendicolare per P alla retta perpendicolare alla retta r passante per P.

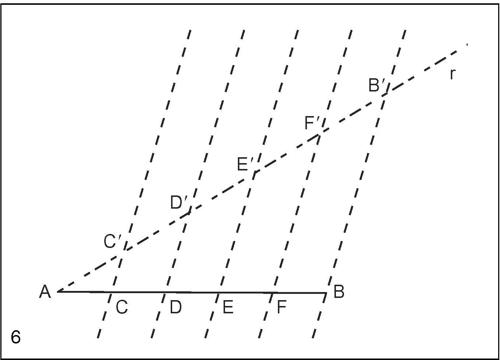
Divisione di un segmento in n parti uguali

Per dividere un segmento AB in parti uguali, per esempio in cinque parti uguali, si traccia una semiretta r per uno dei suoi estremi e su di essa si fissa un punto C′. Con centro in C′ e raggio C′A si determina il segmento C′D′ = AC′. In modo analogo si determinano i segmenti D′E′, E′F′, F′B′, tutti congruenti al segmento AC′. Tracciata la retta BB′, si traccino le parallele a essa per i punti F′, E′, D′, C′. I punti C, D, E, F in cui tali parallele incontrano il segmento dato AB, lo dividono in cinque parti uguali.

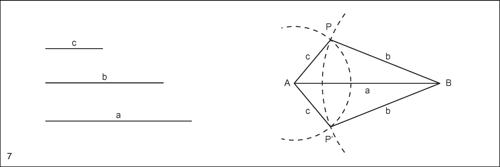
Costruzione di un triangolo di lati assegnati

Dati tre segmenti di lunghezze a, b, c si tracci la circonferenza con centro in un estremo, A, del segmento a e di raggio c e con centro nell’estremo B si tracci la circonferenza di raggio b. Indicati con P e P′ le intersezioni delle due circonferenze, ciascuno dei due triangoli ABP e ABP′ ha per lati i tre segmenti assegnati a, b, c. La costruzione è soggetta a limitazioni sui tre segmenti assegnati. Affinché il triangolo effettivamente esista le due circonferenze devono risultare secanti, comunque sia scelto il segmento sul quale vengono costruite, per cui la somma di due segmenti deve essere maggiore del terzo.

Costruzione di un triangolo rettangolo

Data l’ipotenusa, è sufficiente costruire una semicirconferenza avente l’ipotenusa per diametro. Qualunque punto della semicirconferenza individua il vertice dell’angolo retto del triangolo cercato.

Costruzione di un quadrato inscritto in una circonferenza

Data la circonferenza, si traccia un diametro e, seguendo la procedura per la costruzione dell’asse, si traccia il diametro a esso perpendicolare. I due diametri individuano quattro punti sulla circonferenza che sono i vertici del quadrato.

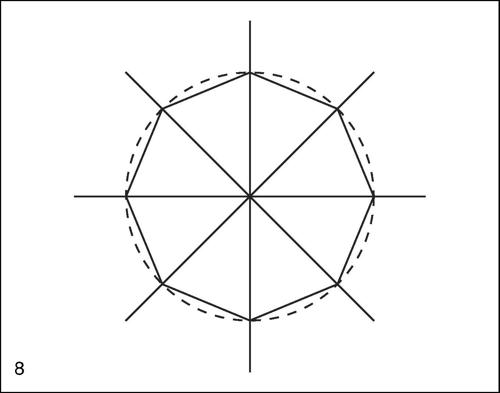
Costruzione dell’ottagono regolare

Tracciati due diametri perpendicolari, si tracciano le bisettrici dei quattro angoli retti da essi individuati: si ottengono complessivamente otto punti sulla circonferenza che sono i vertici dell’ottagono regolare.

Costruzione di un esagono regolare inscritto in una circonferenza

Tracciato un diametro si tracciano dai suoi estremi due semicirconferenze aventi lo stesso raggio della circonferenza che intersecano la circonferenza stessa in quattro punti; questi e i due estremi del diametro scelto sono i vertici di un esagono regolare inscritto nella circonferenza.