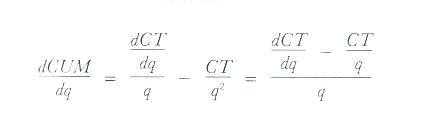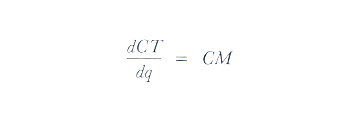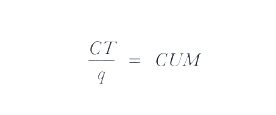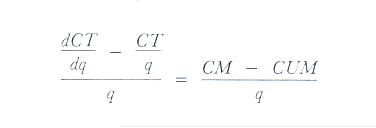Costi
Costi
Definizioni
Il termine 'costi' evoca un senso di sacrificio; indica un onere che è necessario sopportare per conseguire un risultato desiderato. Implicito, nel significato della parola, è il riferimento a un soggetto: non avrebbe infatti senso parlare di sacrifici o di oneri senza avere in mente chi li sopporta. È diverso quindi ragionare di costi riguardanti un singolo individuo, un'impresa, un ente, una collettività. L'ammontare del salario, ad esempio, indica, senza alcun dubbio, un costo per l'impresa che lo sopporta, mentre configura un reddito, e dunque un evento positivo, per il lavoratore; a livello di un intero sistema economico, poi, l'ammontare complessivo dei salari esprime l'entità del prodotto interno lordo ripartito a favore di chi ha prestato la propria opera per ottenerlo. "La quota con cui ciascun fattore è remunerato - affermava Pasquale Jannaccone - è un reddito per quello che la percepisce e un costo per tutti gli altri. Se per ciascun imprenditore sono costi i prezzi che egli paga ai produttori di materie prime e di macchinari, ai lavoratori, ai sovventori di capitali monetari, ai fornitori di servizi pubblici e privati, per ognuna di queste classi di fattori è un costo la quota che rimane nelle mani dell'imprenditore" (v. Jannaccone, 1904). Dato un certo ammontare monetario della produzione, la riduzione della parte dello stesso distribuita a vantaggio di uno o di alcuni fattori produttivi si traduce nell'aumento della parte che residua a favore degli altri. Di conseguenza, parlare di 'costi', senza specificare se si tratta di costi dell'impresa, dell'economia nazionale o del singolo individuo, è come dire nulla. Altrettanto povere di significato sarebbero molte espressioni derivate, sebbene di uso corrente, quale, ad esempio, 'ridurre i costi': è infatti ben diverso cercare di fare ciò per un'impresa o per un sistema economico.Fatta questa precisazione essenziale, si può rilevare come, di norma, il termine 'costi' sia impiegato in rapporto a un'operazione di produzione quale si svolge all'interno di un ente o di un'impresa. Tale termine sintetizza pertanto un concetto largamente utilizzato nel dominio contabile o in quello microeconomico.
I costi in un sistema di controllo
La considerazione dei costi occupa una posizione di assoluto rilievo nell'ambito del sistema contabile posto in essere per controllare i risultati conseguiti nell'esercizio di un'attività economica. È infatti dal confronto tra costi e ricavi, opportunamente impostato e attuato, che deriva la determinazione del guadagno conseguito.La contabilità prevede quindi la predisposizione di metodologie atte ad assicurare un'accurata raccolta ed elaborazione delle informazioni emergenti nel corso di un'attività produttiva o commerciale, in modo da offrire un'adeguata conoscenza e una misura delle conseguenze dei fatti avvenuti. In questo contesto, i costi sono espressioni quantitative e monetarie dei fattori produttivi impiegati nell'esercizio di tale attività.Anche nell'ambito contabile, tuttavia, i costi possono essere considerati a diversi livelli. Essi possono essere infatti rilevati e analizzati con riferimento ad ambiti più o meno estesi e per periodi più o meno ampi. Si possono avere costi riguardanti un'intera impresa, un intero ente o sezioni particolari dei medesimi; costi riguardanti l'intera vita dell'ente o stralci limitati della stessa, come l'anno o il mese. I documenti nei quali possono essere riscontrabili tali diverse configurazioni dei costi sono offerti, a seconda dei casi, dalla contabilità generale o dalla contabilità analitica o industriale.Sotto il profilo della possibilità di controllo, vanno distinti i costi specifici dai costi comuni o generali. I primi sono chiaramente collegabili ai particolari problemi o agli aspetti della realtà di volta in volta rilevanti, riguardino, questi, tipi o volumi di produzione o, ancora, specifiche commesse, singoli beni posti sul mercato, ecc. I secondi sono viceversa indistinti e non chiaramente attribuibili. Possono esserne esempi gli oneri che si sostengono per compiti di coordinamento, per fruire della disponibilità di risorse finanziarie indispensabili per il complesso dell'impresa, per il magazzinaggio e la gestione delle scorte, per servizi utili alle diverse funzioni aziendali. Si tratta non di rado di tipi di costo particolarmente rilevanti e onerosi, difficili da trattare proprio per la scarsa possibilità di imputarli a particolari manifestazioni della produzione.
Tra i costi che hanno la caratteristica di interessare l'attività dell'impresa nel suo complesso, devono essere annoverati in modo particolare quelli afferenti la ricerca. Essi si riferiscono soprattutto a forme di ricerca e sviluppo e hanno particolare consistenza in vista della definizione e della messa a punto di nuovi prodotti da presentare sui mercati. È ben noto come, di norma, per ogni bene fabbricato e venduto siano individuabili delle 'fasi di vita', la prima delle quali riguarda proprio la messa a punto di nuovi prodotti destinati a rinnovare la gamma dell'impresa, in specie quando questa, per certi aspetti, presenta segni di maturità o di rallentamento. In quest'occasione vengono sostenuti costi assai elevati, il cui recupero va ricercato nel collocamento sul mercato di quelli, tra i prodotti studiati, che avranno avuto un buon esito economico.
Dal momento che in una moderna gestione d'impresa la funzione del controllo tende a saldarsi con quella della programmazione (il controllo tende cioè a riscontrare l'aderenza dei risultati consuntivi a quelli programmati), particolare importanza assumono le fattispecie dei 'costi preventivi' o dei 'costi standard'. In prima approssimazione si può affermare che i primi costituiscono una stima, rebus sic stantibus, dei costi futuri, mentre i secondi indicano l'entità dei costi futuri sotto particolari condizioni di efficienza, giudicata raggiungibile. È facile intuire che i costi standard rappresentano la dimensione degli oneri da affrontare per produrre, inserita nella programmazione d'impresa. Al di là dell'importanza assunta dalle rilevazioni e dalle elaborazioni contabili dei costi per una corretta gestione, occorre sottolineare che esse offrono un'indispensabile base conoscitiva per un'analisi corretta dell'economia dell'impresa.
I costi nell'analisi economica
Nell'analisi economica il costo di produzione misura monetariamente quanta parte dei fattori aggregati all'impresa, mediante erogazione o impegno finanziario, ha partecipato concretamente all'azione produttiva. Il costo di produzione esprime dunque l''utilizzazione' dei fattori per ottenere una produzione determinata. Esso si contrappone alla 'spesa' - un fatto esclusivamente finanziario -, dalla quale è quantificato. Sotto questo aspetto il costo di produzione non si differenzia dai diversi fenomeni, positivi e negativi, dell'economia dell'impresa, che, di massima, derivano e sono misurati da eventi di natura finanziaria. Il fenomeno 'costo', non diversamente dal fenomeno 'ricavo', ha natura immateriale. Esso acquista concretezza in virtù di uno specifico evento finanziario, quale può essere un'uscita di cassa o la contrazione di un debito (entrata di cassa o accensione di un credito per il ricavo). Il termine 'spesa' sta a individuare tale aspetto finanziario che si contrappone al termine 'utilizzazione': di questa costituisce l'indispensabile premessa e la misura. Non sempre tra utilizzazione e spesa vi è coincidenza, ma spesso la prima è una quota parte della seconda. Ciò accade allorché fattori aggregati per più cicli produttivi, o per la totalità di un'attività di trasformazione, vengono utilizzati per ottenere volumi di produzione delimitati in particolari intervalli di tempo (anno, semestre) o circoscritti a specifiche sezioni dell'impresa. È il caso degli ammortamenti, che indicano la misura del costo complessivo degli impianti da imputare alla produzione riferita a un certo esercizio o a un determinato settore di attività. Nel caso specifico tale misura deriva da stime della vita media utile dell'impianto o dalla valutazione dell'intensità di utilizzo.
Ancora sotto il profilo strettamente economico, occorre tenere presente che alcuni dei fattori produttivi impiegati possono non avere un'espressione di spesa retrostante che ne consenta un'agevole misurazione. Si pensi a quei fattori che, sebbene utilizzati, non sono stati acquistati, ma sono stati parte dell'organizzazione imprenditoriale fin dal suo sorgere o hanno preso consistenza con il suo stesso evolvere. Ne possono essere esempi il capitale finanziario a titolo di rischio immesso dall'imprenditore nelle fasi iniziali della vita dell'impresa, il lavoro prestato dallo stesso imprenditore, le conoscenze maturate nel corso dell'esercizio dell'attività aziendale ed eventualmente trasferite in brevetti. In casi come questi, i fattori della produzione non hanno un costo contabile: la contabilità infatti non è in grado di registrarlo perché esso non si materializza né in un esborso finanziario, né nell'accensione di un debito, né nell'eventuale alienazione di beni disponibili per acquisire le necessarie risorse. Eppure anche questi fattori devono essere recuperati tramite la produzione ottenuta. I costi di utilizzazione riferibili a tali tipi di fattori sono definiti 'costi impliciti': data la loro mancata registrazione nella contabilità, essi non sono rilevabili in sede consuntiva, ma finiscono in pratica con l'essere inglobati, in bilancio, nella grandezza residuale dell'utile di esercizio. In sede di analisi economica, viceversa, è importante tenerne conto.
L'utilizzazione dei costi in sede decisionale: i modelli costi-volumi di produzione
In una prospettiva operativa la conoscenza dei costi si traduce in una parte del sistema informativo necessario all'operatore per poter effettuare le proprie scelte. Si può affermare anzi che l'analisi dei costi tende in questo senso a saldarsi con la teoria delle decisioni. In accordo con essa, il processo decisionale si articola in alcuni momenti fondamentali così identificabili: a) individuazione completa delle opportunità tra le quali scegliere; b) valutazione delle conseguenze positive e negative che da tali opportunità scaturiscono; c) identificazione e richiamo del sistema degli obiettivi di breve e medio termine ai quali tendere; d) scelta di quell'opportunità per la quale si verifica la maggior aderenza tra conseguenze previste e obiettivi.La conoscenza dei costi è parte del momento della valutazione delle conseguenze delle diverse opportunità che si prospettano all'attenzione dell'imprenditore nel corso dell'attività di gestione. In realtà la materia delle scelte è vastissima e riguarda campi assai diversi. Essa può concretarsi nell'accettare o rifiutare una nuova commessa, nell'entrare in un nuovo mercato, nell'acquisire una nuova tecnologia, nell'ampliare l'assetto produttivo, nel lanciare un nuovo prodotto, nel variare il grado d'integrazione verticale: sono tutti esempi di scelte per le quali l'informazione sui costi ad esse connessi è essenziale. In prima approssimazione si può pensare di collegare a ogni fattispecie in cui l'opportunità o l'alternativa si può manifestare la relativa determinazione di costo. In concreto occorre tuttavia tener presente che tali fattispecie possono essere estremamente numerose, al limite infinite. I livelli ai quali possono tendere l'assetto dimensionale degli impianti, il volume di produzione o il numero di prodotti si presentano infatti assai numerosi; rischia quindi di rivelarsi sostanzialmente impossibile o estremamente lungo e faticoso cercare di conoscerne gli oneri conseguenti, identificabili nei costi. Si pone in questa prospettiva l'esigenza di pervenire a modelli descrittivi, sufficientemente generali, in grado di cogliere l'eventuale legame esistente tra le diverse opportunità e i costi relativi.
Non tutte le opportunità che in concreto si presentano all'operatore sono tuttavia suscettibili di una sintesi atta a essere introdotta in un modello generalizzabile: molto spesso esse sono infatti individuabili e descrivibili soltanto in termini qualitativi e con una rilevante abbondanza di elementi non riducibili a un unico parametro di misura. Si rende necessario perciò fare ricorso a modelli facilmente trattabili per quei problemi che a tal fine si rivelino adatti, ingegnandosi di avvalersi di altri approcci interpretativi per l'analisi di tematiche meno descrivibili tramite schematizzazione.
Nasce pertanto l'esigenza di individuare le eventuali connessioni tra utilizzazione dei fattori produttivi e una variabile indipendente quale la quantità prodotta di un determinato bene o il volume del fatturato. Ove un collegamento di questo tipo sia tradotto formalmente in un modello appropriato, i diversi livelli di costo potranno essere conosciuti mediante semplice immissione dei dati di input, ossia dei diversi livelli dimensionali dell'attività produttiva. Diviene pertanto possibile descrivere a priori le conseguenze negative derivanti dai diversi volumi di produzione e analizzarle, eventualmente, in rapporto ad altre eventuali problematiche emergenti.
Su una linea metodologica di questo tipo può avvenire, almeno in prima approssimazione, il recupero del celebre schema di derivazione neoclassica della relazione costi-volumi di produzione. In realtà tale ripresa è limitata all'intelaiatura concettuale, poiché, come si avrà modo di mettere in evidenza, alcuni aspetti dello schema ricordato non reggono il confronto con la realtà. Quanto occorre è infatti uno strumento d'interpretazione, operativo e funzionale, utilizzabile per molte delle decisioni imposte dalla conduzione dell'impresa.
La teoria neoclassica dei costi di produzione
Sono state prospettate diverse ipotesi sulle relazioni fra costo totale e volume della produzione. Si è ipotizzato che il costo totale cresca in proporzione, più che in proporzione o meno che in proporzione rispetto alla produzione: nel primo caso si presuppone una produttività costante dei fattori produttivi, nel secondo una produttività decrescente, nel terzo una produttività crescente.Originariamente si supponeva che la produttività costante sarebbe stata prerogativa delle attività artigianali, che impiegavano prevalentemente lavoro immediato o fattori variabili, quella crescente delle manifatture in genere, mentre quella decrescente avrebbe caratterizzato l'agricoltura, come qualunque attività tesa a combinare fattori variabili con fattori fissi disponibili però in misura limitata. La teoria neoclassica ha viceversa integrato i diversi andamenti della produttività riferendoli all'impresa di una qualsiasi attività produttiva. Più in particolare, gli economisti neoclassici hanno distinto il breve dal lungo periodo, una distinzione che tuttavia ha carattere logico e non cronologico: nel 'breve periodo' si assume che gli impianti siano dati, nel 'lungo' che possano essere modificati.
Per ora si fa riferimento al breve periodo, o breve termine, e si assumono come dati gli impianti. In queste condizioni secondo la teoria neoclassica la combinazione tra fattori variabili (materie prime, energia, lavoro diretto) e fattori fissi (gli impianti e l'apparato amministrativo) darebbe luogo a una produttività crescente fino a un certo punto - il punto cui corrisponde la combinazione ottima -, una produttività ipoteticamente costante in questo punto e una produttività decrescente dopo quel punto.
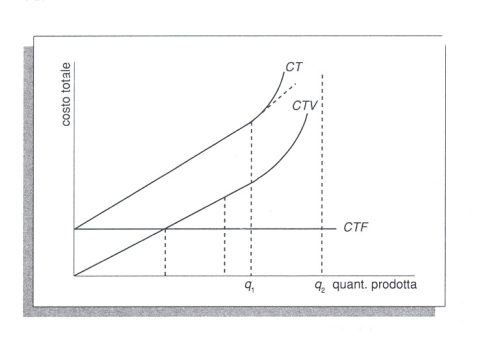
Secondo la teoria neoclassica la tipica funzione del costo totale assume pertanto la forma di una esse rovesciata. La sua lettura indica la presenza di un certo ammontare di costi totali fissi (CTF) collegabili alla struttura dell'impresa. A partire dall'origine degli assi si sviluppa l'andamento del costo totale variabile (CTV), espresso dalla funzione
CTV= f(q),
dove q è la quantità prodotta.Quindi la funzione del costo totale complessivo può essere sintetizzata nell'espressione
CT = CTF + f(q).
Nel breve termine la non proporzionalità fra variazioni dei costi e variazioni della produzione dipende esclusivamente dall'andamento del costo variabile totale.Tali fenomeni possono essere meglio compresi passando ad altre configurazioni di costo, derivanti dalla funzione di costo totale e proponibili per l'approfondimento di determinati problemi, tipici della gestione d'impresa. Si tratta del costo marginale e del costo unitario medio, entrambi rappresentabili come funzioni della quantità prodotta.
Costi unitari medi e costi marginali
Il costo unitario medio (CUM) è espresso dal rapporto tra il costo totale (CT) e il volume della quantità prodotta (q). Si ha cioè:
CUM = CT/q.
Il significato del costo unitario medio è semplice e riconducibile a quello di una media aritmetica: ottenuta una determinata quantità di produzione, esso indica quale carico di fattori produttivi gravi su ognuna delle unità che la compongono. Anche a livello di costo unitario medio è riconoscibile e separabile l'effetto dei costi che, nella configurazione di costo totale, sono individuabili come fissi o variabili. Si ha perciò il costo unitario medio fisso (CUMF), espresso da
CUMF = CTF/q,
e il costo unitario medio variabile (CUMV), espresso da
CUMV = CTV/q.
Il costo unitario medio ha un preciso valore per ogni determinazione della quantità prodotta: è possibile pertanto tracciarne l'andamento grafico separatamente per le sue componenti essenziali.
Si comprende facilmente che l'andamento del costo unitario medio fisso è quello di un'iperbole equilatera: lungo tutti i suoi punti essa verifica infatti la costanza dei costi fissi totali come prodotto del costo unitario medio fisso (decrescente) per la quantità prodotta (crescente).L'andamento del costo unitario medio variabile è collegato all'andamento del costo variabile totale: decrescente, costante e crescente rispettivamente quando quest'ultimo cresce meno che proporzionalmente, proporzionalmente e più che proporzionalmente rispetto al crescere della produzione. Il CUM risulta dalla composizione dei due andamenti del CUMF e del CUMV.
Di significato diverso, benché sempre espresso a livello unitario, è il costo marginale (CM). Esso è definito come la variazione del costo totale derivante da una variazione molto piccola (a rigore infinitesima) della produzione. Il concetto così espresso trova traduzione analitica nella derivata della funzione del costo totale:
CM = dCT/dq.
In termini geometrici il costo marginale (CM) indica l'inclinazione della curva del costo totale. Essa coincide, in ogni punto, con la tangente trigonometrica dell'angolo formato dalla tangente geometrica alla curva con la parallela all'asse delle ascisse che passa per il punto. Nella fase iniziale, caratterizzata dalla produttività crescente, agli aumenti della produzione corrisponderanno incrementi via via minori del costo totale, mentre tali incrementi diverranno prima costanti e successivamente via via maggiori con l'entrata nella fase di produttività decrescente. Da un punto di vista logico, il costo marginale porta l'analisi su ipotesi successive (incrementi di quantità prodotta), laddove il costo unitario medio porta l'analisi su ipotesi alternative. In questi due distinti caratteri stanno le rispettive potenzialità di applicazione: utile il costo marginale per concentrare l'attenzione su quanto differenzia un assetto dimensionale dall'altro (ad esempio per decidere se accettare o meno una nuova commessa o se praticare o meno una variazione di prezzo), utile il costo unitario medio per disporre con rapidità di indicazioni di sintesi (ad esempio per avere orientamenti in vista della determinazione di un prezzo). Definiti i concetti, la considerazione simultanea degli andamenti del costo totale medio, del costo variabile medio e del costo marginale consente di comprendere l'intreccio tra gli stessi e il manifestarsi dei diversi regimi di produttività.
È possibile analizzare infine i rapporti fra costo variabile medio e costo marginale. Se la produttività dei fattori variabili è costante, non c'è differenza fra costo variabile medio e costo marginale, dato che il secondo è anch'esso un costo variabile: in regime di produttività costante il costo marginale è costante e coincide con il costo variabile medio. Se, come ipotizza la teoria neoclassica tradizionale, la produttività è in un primo tratto crescente e in un secondo tratto decrescente, allora i due costi - variabile medio e marginale - non coincidono. Dai livelli iniziali entrambi i costi tendono a diminuire: il costo marginale tende a diminuire per tutto il tratto della produttività crescente; il costo variabile medio, invece, proprio perché rappresenta una media dei costi marginali, diminuisce fino a quando la somma dei costi marginali decrescenti supera la somma dei costi marginali in crescita. Quando la seconda supera la prima, anche il costo variabile medio comincia a crescere. Il costo fisso unitario diminuisce al crescere della quantità prodotta. Il costo unitario medio, dato dalla somma del costo unitario fisso e del costo variabile medio, diminuisce, in un primo tratto, sia per la diminuzione del costo unitario fisso sia per quella del costo variabile medio; dopo un certo punto, la crescita del CUMV compenserà e supererà la diminuzione del CUMF; dopo quel punto anche il CUM tende a salire. Si intuisce da queste considerazioni che la curva del costo marginale taglia la curva del costo unitario medio nel punto di minimo. Ricorrendo alle derivate, si può tuttavia darne la seguente agevole dimostrazione.
Affinché il CUM sia minimo, occorre che la sua derivata prima rispetto a q sia nulla e che la derivata seconda sia maggiore di zero.
Limitando l'asserzione alla prima di tali condizioni, si avrà
ma, per definizione,
e
dal momento che nel punto di intersezione delle rispettive curve il CUM e il CM, ovviamente, sono uguali, in tal punto il numeratore della
si annulla: c.v.d.
Va notato infine che gli andamenti testé descritti ripropongono all'attenzione del lettore il noto andamento a U che, stante l'andamento del costo totale, caratterizza sia il CM che il CUMV e il CUM. Per quanto riguarda queste ultime due grandezze, va sottolineato che sono diversi sia il livello del costo che il volume di produzione in corrispondenza dei quali si collocano i rispettivi punti di minimo. Nel caso del CUM, infatti, il punto di minimo appare più a destra lungo l'asse delle ascisse e più in alto lungo l'asse delle ordinate. Solo in corrispondenza con la quantità q₃ si ha infatti la perfetta compensazione tra le diseconomie derivanti dalla produttività decrescente, evidente per i fattori variabili fin dal punto q₁, e le economie che derivano dalla ripartizione dei costi fissi su volumi sempre più ampi di produzione; da quel momento in poi anche il CUM sarà crescente. Sia per il costo unitario medio variabile sia per il costo unitario medio, la forma a U della curva riflette la 'legge dei rendimenti decrescenti', che tende a caratterizzare i fattori variabili della produzione nel loro insieme.
Critiche all'impostazione tradizionale
L'impostazione ora descritta presta il fianco ad alcune critiche, essenzialmente suggerite dal suo mancato riscontro nella realtà aziendale. In particolare, non sembra che corrisponda alla realtà l'andamento a U del costo marginale, che sembra piuttosto avere la forma di una retta. Ma se il costo marginale è costante esso non è distinguibile dal costo variabile medio. Un costo marginale costante presuppone una produttività costante dei fattori variabili; questo, appunto, sembra avvenire nelle imprese, pur essendo dati gli impianti. In effetti, le variazioni del grado di utilizzazione degli impianti comportano variazioni in senso inverso del costo fisso per unità, ma non influiscono, di norma, sulla produttività dei fattori variabili.
Già alla fine degli anni trenta, George Stigler avanzava l'ipotesi che il costo unitario medio variabile (CUMV) assumesse per un lungo intervallo, corrispondente alla zona di sfruttamento 'normale' della capacità produttiva, un andamento costante, per crescere poi rapidamente in prossimità del pieno sfruttamento della capacità produttiva installata.
Il contrasto con l'ipotesi descritta nel capitolo precedente, secondo cui l'andamento dei costi unitari medi variabili sarebbe fino a un certo punto decrescente e poi crescente, è evidente. Prescindendo per semplicità da un eventuale tratto iniziale in cui il costo unitario medio variabile tende a decrescere per effetto di una migliore organizzazione dei fattori variabili stessi, è il regime di produttività costante a definire, in condizioni di normale sfruttamento della capacità produttiva, l'andamento del costo unitario medio variabile. Solo dopo il punto q₁ la curva del costo unitario medio variabile tende a crescere, a causa degli inevitabili oneri aggiuntivi (maggiore costo del lavoro per gli straordinari, maggiori sprechi e scarti di materiale, maggiori costi di manutenzione) connessi a uno sfruttamento 'intensivo' della capacità produttiva installata.Coerentemente con l'impostazione assunta, nell'intervallo da 0 a q₁ la curva del costo marginale (CM) si sovrappone alla curva del costo unitario medio variabile (CUMV) e solo dopo il punto q₁ i costi marginali tendono a crescere, mantenendosi ovviamente a un livello superiore rispetto ai costi unitari medi variabili. Data l'usuale iperbole che rappresenta l'andamento del costo unitario medio fisso, il costo unitario medio decresce fino al punto q₁, per effetto della migliore ripartizione dei costi fissi totali, invertendo la tendenza dopo tale punto, a causa della crescita del costo unitario medio variabile, solo parzialmente compensata da un'ulteriore riduzione della componente fissa per unità di prodotto. Nella fig. 6 sono riportati, infine, gli andamenti del costo totale fisso (CTF), del costo totale variabile (CTV) e del costo complessivo (CT), secondo la concezione descritta. Il costo totale variabile cresce linearmente sino al punto q₁, per poi crescere, dopo tale quantità, più che proporzionalmente rispetto alla produzione, mentre la curva del costo totale complessivo decorre parallelamente a quella del costo totale variabile, a una distanza pari all'ammontare del costo totale fisso.Rispetto all'ipotesi tradizionale, che suppone un andamento a U sia del costo medio variabile sia del costo marginale, l'ipotesi di un andamento costante, almeno fino a un certo punto (fino alla quantità q₁), di entrambi questi costi appare più vicina alla realtà; la stessa crescita dei due costi - crescita assunta da alcuni economisti e negata da altri - intorno al pieno sfruttamento degli impianti può sembrare plausibile. Occorre tuttavia osservare, come meglio verrà chiarito più avanti trattando delle funzioni lineari di costo, che, nella realtà dell'impresa, il tratto dei rendimenti decrescenti, quand'anche esista, tende a essere evitato: al manifestarsi dei primi rendimenti decrescenti le direzioni aziendali scelgono di mutare il proprio assetto produttivo, così da riportarsi nella situazione caratterizzata da rendimenti e costi marginali costanti.
Il passaggio al lungo termine
Le considerazioni finora svolte sono fondate sull'ipotesi di un assetto produttivo e di impianti dati. In esse gli andamenti dei costi totali, unitari medi e marginali sono stati infatti studiati con riferimento a una realtà d'impresa esistente, all'interno della quale si è proceduto all'analisi di volumi di produzione ottenibili con la capacità produttiva disponibile. Se invece si ammette che gli impianti e, più in generale, la capacità produttiva possano essere modificati, si passa dalla considerazione del breve termine a quella del lungo termine; nella seconda ipotesi, sono variabili anche i costi relativi agli impianti e all'apparato amministrativo. Nella scelta fra diverse capacità produttive, cui corrispondono diverse tecniche, si assume che la tecnologia non vari: il progresso tecnico, infatti, richiede una diversa analisi.
Secondo la teoria tradizionale, anche la curva che rappresenta la funzione del costo unitario medio di lungo termine avrebbe un andamento a U. La detta curva è l'inviluppo di una successione continua di curve rappresentanti funzioni di breve termine, ossia è la curva tangente all'infinita successione ipotizzabile delle curve di breve termine. Ciascuna di queste corrisponde a un'ipotesi diversa e alternativa di capacità produttiva, nonché alla combinazione di fattori relativa. In tale impostazione si afferma che la curva di lungo termine riporta i risultati dell'esplorazione sistematica di tutte le possibilità di produzione esistenti e deriva dall'unione dei punti di ottima convenienza per ciascuno dei volumi di produzione ipotizzabili. Occorre sottolineare che la situazione di massima convenienza di una determinata quantità non cade in corrispondenza dei punti di minimo delle singole curve di breve termine: nella fig. 7 la quantità qE potrebbe essere prodotta con la struttura di produzione identificata dalla curva FF´, che, per quella quantità, presenterebbe il minimo. In realtà a essa è preferibile la struttura corrispondente alla curva EE´, poiché i costi a essa collegabili, pur essendo in fase di andamento crescente, per la quantità anzidetta, qE, si presentano inferiori al punto di minimo della curva FF´. Le curve di lungo termine identificano cioè i livelli di costo minori per i diversi volumi di produzione, in base alle tecnologie esistenti. La coincidenza della curva di lungo termine con il punto di minimo di una curva di breve termine avviene solo in corrispondenza della quantità per la quale si manifesta il minimo tra tutti i minimi delle curve di CUM di breve termine.Al di fuori di questo caso, ove s'intendesse unire con la curva di lungo termine tutti i punti di minimo delle curve di breve termine, si verificherebbero degli incroci. Il costo leggibile sulla curva di breve periodo per le diverse quantità sarebbe in tal caso inferiore a quello giacente sulla curva di lungo termine, in contrasto con l'ottimizzazione che, proprio attraverso la rimozione dei limiti del breve termine, viene ricercata. Secondo la teoria tradizionale, la curva del costo medio di lungo termine avrebbe un andamento a U, giacché in un primo tratto opererebbero le cosiddette economie di scala, tecnologiche e amministrative, che consistono in risparmi di costi ottenibili, fino a un certo punto, col crescere delle dimensioni; in un secondo tratto, però, prevarrebbero le diseconomie di scala, dovute alle crescenti difficoltà burocratiche e organizzative. Una tale concezione è stata criticata, in primo luogo, in quanto è incompatibile con la concorrenza atomistica, che gli economisti neoclassici considerano come la forma di mercato normale: economie e diseconomie di scala sono difatti incompatibili con imprese di dimensioni molto piccole. Inoltre, indipendentemente dalla forma di mercato, è stato messo in dubbio che i costi unitari medi di lungo periodo dopo un certo punto debbano necessariamente crescere. Certo, se una tale crescita non ha luogo, il limite all'espansione dell'impresa non proviene dai costi, ma dalla curva di domanda; in effetti, in condizioni di mercato non concorrenziali, la curva di domanda può ben essere inclinata negativamente rispetto alla singola impresa.
L'approssimazione lineare
L'analisi critica dell'impostazione neoclassica prende spunto dall'osservazione di come i costi si manifestino nella realtà.Per corrispondere alle esigenze di un'analisi economica che non intenda discostarsi dalla concretezza occorre tuttavia progredire nella conoscenza fino a esprimere in forma analitica, determinata e trattabile, le relazioni presentate come frutto di intuizione e, in ultima analisi, in termini prevalentemente qualitativi.Impresa per impresa, produzione per produzione, si può tentare di individuare l'andamento dei costi mediante interpolazione e successiva definizione di funzioni statistiche di costo. In tali casi i costi (totali, unitari medi o marginali) sono considerati variabili dipendenti dalla quantità prodotta (variabile indipendente) e collegate a quest'ultima mediante un vincolo preciso.
Frequentemente usati e concordemente giudicati rispondenti alla pratica aziendale sono i modelli di tipo lineare, i cui parametri sono stimati di norma mediante il metodo dei minimi quadrati.In pratica si esaminano i dati forniti dalla contabilità industriale e si rilevano le diverse quantità prodotte in passato in unità di tempo prestabilite (anni, trimestri, mesi, quindicine) unitamente ai livelli dei costi totali sostenuti per produrre ciascuna quantità. Si viene in tal modo a disporre di due serie di dati legate da un vincolo di natura tecnica, per cui al mutare degli uni corrisponde una variazione negli altri. La regressione statistica mira a dare a questo vincolo un'espressione analitica. A tal fine le due serie di dati vengono disposte su un sistema di assi cartesiani in cui si riportano rispettivamente sull'asse delle ascisse i diversi volumi di produzione e sull'asse delle ordinate i costi che a essi si riferiscono. Per ogni valore riportato sull'asse delle ascisse, si segna l'ammontare del relativo costo totale sull'asse delle ordinate.
Si ottiene così un insieme di punti dispersi nel primo quadrante, tra cui si inserisce la retta che meglio li interpola. Quando si disponga di una serie sufficientemente ampia di rilevazioni empiriche attinenti combinazioni quantità-costo totale, è possibile pervenire alla costruzione di una funzione lineare di costo totale (CT) mediante l'applicazione del metodo dei 'minimi quadrati ordinari' (nella terminologia econometrica anglosassone OLS, Ordinary Least Squares). Lo strumento (descritto in qualunque buon manuale di statistica) permette d'individuare, tra le infinite rette che passano per la nuvola dei punti rilevati empiricamente, quella 'ottimale', intendendosi con questo termine la retta che rende minima la somma dei quadrati degli scarti tra i dati rilevati e i dati della stima (non è quindi esclusa l'esistenza di funzioni, diverse dalla retta, sotto questo aspetto migliori). Indicando con qi, i=1,...,n, le quantità rilevate e con CTi, i=1,...,n, i costi totali rilevati, si perverrà alla seguente stima della funzione di costo totale: in cui CT* sta a indicare il costo totale perequato (variabile dipendente), ¯¯CT la media dei costi totali effettivamente offerti dalla contabilità analitica, qi la iesima quantità prodotta (variabile indipendente) e q̄ la media delle quantità rilevate.
I modelli fondati sull'andamento lineare dei costi sono largamente entrati nella pratica a causa della grande semplicità d'uso. Basti ricordare la possibilità di conoscere i costi variabili mediante una semplice traslazione dell'asse delle ascisse e quindi la conseguente rapidità di determinazione del costo variabile unitario medio, coincidente in questo caso con il costo marginale. Dalla pratica le funzioni lineari hanno fatto il loro ingresso nella teoria economica e negli studi statistici. In molti saggi, anzi, le funzioni lineari di costo sono dette 'funzioni statistiche' per antonomasia.
Tale 'trasferimento' dalla prassi alle sedi teoriche offre una tangibile dimostrazione dell'approccio 'induttivo' attraverso cui la teoria microeconomica ha compiuto i più recenti significativi progressi. Si tratta invero di un nuovo modo di guardare a questi fenomeni e di tentare delle generalizzazioni capaci di consentire risultati operativi.
Non sono mancate prese di posizione critiche nei confronti dell'approssimazione lineare. Secondo alcuni studiosi (R. Ruggles), l'andamento lineare dei costi deriva essenzialmente dalla natura dei dati disponibili e dai metodi contabili e statistici adottati. Si tratta di osservazioni logiche e motivate. Esse possono tuttavia, entro certi limiti, essere superate grazie ai progressi compiuti sia nelle tecniche di rilevazione dei dati, sia nelle metodologie statistiche ed econometriche.
Un'altra obiezione riguarda i criteri di ammortamento. Siccome in molti casi questi sono basati sull'ipotesi di un logorio indipendente dall'intensità di utilizzo, e quindi di un conseguente deprezzamento dei beni strumentali proporzionale al loro valore, ne deriva l'imputazione di un costo fisso per gli impianti. Questo procedimento condurrebbe alla definizione artificiosa di un costo marginale costante, qualora invece il logorio aumentasse, e in misura più che proporzionale, al crescere dell'intensità di sfruttamento delle capacità produttive disponibili. Tuttavia questa obiezione può venire superata in base alla considerazione che oggi le politiche di ammortamento devono sempre più tenere conto del fattore obsolescenza economica piuttosto che del puro logorio tecnico degli impianti: è pertanto ragionevole che le quote siano tendenzialmente costanti.
A essere messa in crisi, nelle critiche alle funzioni lineari, è la dicotomia tra costi fissi e costi variabili, che non è affatto netta come normalmente viene considerata. Qualunque utilizzazione di fattore produttivo avrà un costo fisso o variabile a seconda che la si consideri nel breve o nel lungo periodo. È dato di osservazione comune che i costi derivanti dagli impianti, considerati fissi per antonomasia, sono effettivamente tali unicamente nel breve termine. Nel lungo periodo essi tendono invece a crescere col crescere della capacità produttiva. Il discorso vale altresì, in senso inverso, per quei costi solitamente considerati variabili: ad esempio per il lavoro o per i consumi di materie prime. Oscillazioni di breve periodo nella quantità ne lasciano cioè inalterato il livello totale. Quando, ad esempio, si assumono nuove forze di lavoro, si aggrega all'impresa una nuova capacità di produzione. Anche in relazione a questa capacità si manifesterà un livello ottimale di sfruttamento che l'impresa tenderà a raggiungere. Fino a quantità vicine a tale livello, inferiori o superiori a esso, il costo totale sostenuto non subirà mutamenti: esso cioè sarà fisso. Lo stesso accade per le materie prime, che, per esigenze di approvvigionamento, o per i loro stessi caratteri tecnologici, vengono acquistate non nella misura minima necessaria alla produzione che si intende ottenere, bensì in quantità normalmente maggiori di quelle effettivamente necessarie.In realtà i caratteri 'fisso' e 'variabile' non sono attributi esclusivi di particolari tipi di costo derivanti da precisi fattori di produzione; essi sono invece riscontrabili in diversa misura nei costi derivanti da qualsiasi fattore.
A fronte di tale constatazione, l'idoneità delle funzioni lineari di costo a rispecchiare le effettive relazioni costi-volumi di produzione può apparire discutibile. Esse tendono infatti a isolare un volume di costi fissi e ad attribuire a tale volume carattere di rigidità per un intervallo di tempo comune a tutti i fattori di produzione.Pur nella consapevolezza di tali limiti, è tuttavia necessario ricordare l'utilità di tali funzioni come strumenti interpretativi delle evidenze empiriche, anche tenendo conto del fatto che: 1) nella maggior parte dei casi in cui sono stati applicati i test statistici per lo studio della significatività, l'ipotesi della linearità non è stata respinta; 2) molto spesso, correggendo la relazione con l'aggiunta di termini quadratici o cubici, non sono stati apportati dei miglioramenti apprezzabili.Sul piano teorico, infine, l'andamento lineare dei costi sembra cozzare contro l'assunto della produttività decrescente, considerato nelle funzioni di costo studiate in microeconomia. A supporto di tale assunto si richiama l'esistenza dei costi di manutenzione straordinaria quando lo sfruttamento degli impianti supera determinati livelli d'impiego, oppure ancora il logorio e l'invecchiamento dei macchinari a mano a mano che si procede verso la saturazione della casiderazione di momenti eccezionali della vita dell'impresa, nei quali l'attività è vicina alla saturazione della capacità produttiva disponibile; non è quindi il caso di tener conto di questi momenti nella valutazione di quella che l'esperienza empirica presenta come una condizione mediamente normale.
D'altro canto, non di rado, i costi che esprimerebbero spinte verso la produttività decrescente (costi promozionali, amministrativi, di ricerca) presentano legami piuttosto tenui con l'andamento della produzione. Limitando l'osservazione al solo breve termine, si finisce con il soffermarsi su momenti di vita dell'impresa che si svolgono entro condizioni e intervalli dati, durante i quali tali costi tendono a essere costanti, mentre varierebbero nel passaggio da un intervallo a quello successivo.
L'analisi delle critiche mosse alla linearità dei costi e le ricerche empiriche condotte su base rigorosa a livello di settore e a livello di singola impresa consentono di concludere che, entro i limiti della capacità produttiva di un'impresa esistente a un tempo t, e quindi entro un'ottica di breve termine, l'andamento dei costi totali può essere rappresentato con sufficiente attendibilità da funzioni di tipo lineare.Nel breve termine l'andamento del costo totale CT può quindi essere descritto da relazioni del tipo CT = CTF + CUMV · q, dove CTF indica l'ammontare dei costi fissi, CUMV è il costo unitario medio variabile e q indica la quantità prodotta.Dato il carattere lineare dell'espressione, la distinzione tra costo marginale e costo unitario medio variabile cessa di esistere: il costo unitario medio variabile CUMV è uguale al costo marginale e costante al variare dei volumi di produzione. Come già s'è avuto modo di sottolineare, il costo marginale costante è sostanzialmente coerente con la stessa prassi della gestione dell'impresa industriale. Quando i direttori amministrativi qualificano come 'variabili' determinati tipi di costo, intendono, con questo aggettivo, descrivere una variabilità proporzionale al variare della produzione. Ciò implica la costanza del costo marginale.Le situazioni dalle quali possono discendere manifestazioni di produttività decrescente e pertanto costi variabili più che proporzionalmente al variare dei volumi di produzione hanno di norma carattere eccezionale e preludono a cambiamenti destinati a riportare le dinamiche nell'ambito del regime della produttività costante.
Ciò è vero anche per il lungo termine, dove non sempre l'ampliamento degli impianti è foriero di miglioramenti importanti in termini di efficienza. In molti casi l'adeguamento delle capacità produttive comporta modificazioni non rivoluzionarie. Le nuove acquisizioni danno perciò origine ad aumenti nei costi totali fissi che, in corrispondenza di livelli di utilizzazione giudicati ottimali, conducono a valori sostanzialmente simili del costo unitario medio. Quando si considerino i volumi di produzione raggiungibili in concreto, e quindi il passaggio da livello ottimale a livello ottimale di utilizzazione di una successione di ampliamenti della capacità produttiva, l'andamento del costo unitario medio, dopo una prima fase in cui decresce, tende a divenire costante nel lungo termine. Del pari tende a divenire costante il costo marginale di lungo termine. Un abbassamento del costo unitario medio si verificherebbe solamente in corrispondenza di adeguamenti della capacità produttiva dai quali derivassero apprezzabili progressi in termini di produttività. Si produrrebbero in tal caso le economie di scala, le cui manifestazioni sono in pratica discontinue.In ogni caso occorre ancora sottolineare che quella della linearità è un'ipotesi d'uso operativo e quindi può anche contenere un certo margine di errore. Stabiliti determinati limiti oltre i quali non conviene andare, si possono tollerare errori di lieve entità, che, in quanto tali, non inficiano i risultati. L'influenza dei costi crescenti per l'azione della produttività decrescente, negli intervalli normalmente presi in considerazione, potrebbe quindi far deviare l'andamento dei costi variabili da quello della retta, soltanto per percentuali molto piccole e come tali trascurabili per fini operativi.
Quando sia noto il prezzo dei prodotti presentati sul mercato, le relazioni lineari dei costi consentono di delineare delle sintesi traducibili in modelli estremamente semplici, utili a descrivere alcuni problemi ricorrenti e passibili altresì di sviluppi operativi nella gestione d'impresa.Celebre e largamente utilizzata, con riferimento al breve periodo, è l'analisi del punto di pareggio (break-even analysis). Accertata la funzione di costo totale lineare CT=CTF+CUMV ·q, e noto che sia il prezzo di vendita del prodotto, viene definita la funzione di ricavo totale, pure essa lineare e passante per l'origine: RT=pq, dove RT indica il ricavo totale, p il prezzo esistente sul mercato e q il volume di produzione. Nel sistema che ne risulta, ponendo RT=CT e risolvendo rispetto a q, si ha che esprime la condizione per la quale si verifica l'eguaglianza tra costi e ricavi totali. L'importanza di quest'espressione risulta chiara quando se ne esamini il significato logico: dal momento che ogni unità prodotta e venduta reca alla gestione un beneficio definito 'margine di contribuzione', pari alla differenza tra prezzo e costo variabile unitario (nell'ovvia ipotesi in cui p>CUMV), il pareggio tra costi e ricavi globali verrà raggiunto allorché la somma dei vantaggi differenziali derivanti dal cumularsi delle quantità, a mano a mano che da zero si procede verso la saturazione della capacità produttiva disponibile, compenserà completamente l'ammontare dei costi di struttura (CTF) indipendenti dal volume di produzione. Tale logica è rispecchiata graficamente nella linea del profitto UN=(p-CUMV)q-CTF che interseca l'asse delle ascisse nel punto q*. Per una quantità di produzione nulla il profitto vale -CTF; in corrispondenza della quantità di produzione q* il profitto vale 0, cioè si ha l'eguaglianza tra costi e ricavi totali.
È chiaramente comprensibile quanto sia rilevante, in concreto, la determinazione della quantità q*. Essa indica all'operatore quanto, con la struttura della quale dispone, deve produrre come minimo per non dover subire perdite di gestione e incorrere quindi nei rischi e negli inconvenienti relativi. (V. anche Contabilità aziendale; Offerta; Produzione).
Bibliografia
Allen, R.G.D., Mathematical analysis for economists, London 1938 (tr. it.: Analisi matematica per economisti, Milano 1979²).
Asimakopulos, A., An introduction to economic theory, TorontoOxford-New York 1978 (tr. it.: Microeconomia, Bologna 1982).
Baumol, W.J., Economic theory and operation analysis, Englewood Cliffs, N.J., 1952 (tr. it.: Teoria economica e analisi operativa, Milano 1968).
Bilas, R.A., Microeconomic theory, Tokyo 1971.
Bresciani-Turroni, C., Corso di economia politica, vol. I, Milano 1967.
Brigham, E.F., Pappas, J.L., Managerial economics, London 1974.
Castellino, O. e altri, Che cosa produrre, come e per chi, Torino 1983.
Clapham, J., Of empty economic boxes, in "The economic journal", 1922, XXXII, pp. 305-314 (tr. it. in: Contributi per un'analisi economica dell'impresa, a cura di G. Zanetti, Napoli 1980, pp. 160-169).
Dean, J., Methods and potentiality of break-even analysis, in Studies in cost analysis (a cura di D. Solomons), London 1968, pp. 245-246.
Dorfman, R., Samuelson, P.A., Solow, R.M., Linear programming and economic analysis, New York 1958.
Ferrer-Pacces, F.M., I sistemi d'impresa, Torino 1974.
Frisch, R., Lois techniques et économiques de la production, Paris 1963 (tr. it.: Leggi tecniche ed economiche della produzione industriale, Milano 1966).
Gravelle, H., Rees, R., Microeconomics, London-New York 1981.
Graziani, A., Teoria economica. Prezzi e distribuzione, Napoli 1976.
Gros-Pietro, G.M., Intorno alla natura del divario fra teoria e pratica nelle decisioni d'impresa, in "Ratio", 1971, n. 2, pp. 155-176.
Henderson, H., Quandt, R.E., Microeconomic theory. A mathematical approach, New York 1958 (tr. it.: Teoria microeconomica, Torino 1973).
Jannaccone, P., Il costo di produzione, Torino 1904.
Johnston, J., Statistical cost functions: a reappraisal, in "Review of economics and statistics", 1958, XL, pp. 339-350.
Kaldor, N., The equilibrium of the firm, in "The economic journal", 1934, XLIV, pp. 60-76 (tr. it. in: Contributi per un'analisi economica dell'impresa, a cura di G. Zanetti, Napoli 1980, pp. 305-320).
Koutsoyiannis, A., Modern microeconomics, London 1981 (tr. it.: Microeconomia, Milano 1981).
Malinvaud, E., Leçons de théorie microéconomique, Paris 1971.
Robinson, A., The problem of management and the size of firms, in "The economic journal", 1934, XLIV, pp. 242-257 (tr. it. in: Contributi per un'analisi economica dell'impresa, a cura di G. Zanetti, Napoli 1980, pp. 321-337).
Ruggles, R., The concept of linear total cost-output regressions, in "American economic review", 1941, XXXI, pp. 332-335.
Stigler, G., Production and distribution in the short run, in "Journal of political economy", 1939, XLIX, pp. 305-327.
Sylos Labini, P., Oligopolio e progresso tecnico, Torino 1971.
Varian, H.R., Microeconomic analysis, London-New York 1978.
Wieiner, J., Separation of fixed and variable cost, in "The accounting review", 1960, XXXV, pp. 686-698.
Wonnacott, R. J., Wonnacott, Th. H., Econometrics, New York 1970 (tr. it.: Trattato di econometria, Milano 1974).
Zanetti, G. (a cura di), Contributi per un'analisi economica dell'impresa, Napoli 1980.
Zanetti, G., Economia dell'impresa, Bologna 1985.