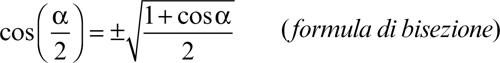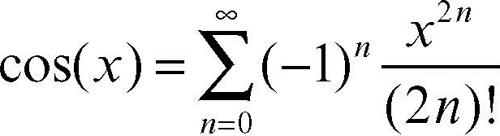coseno

coseno

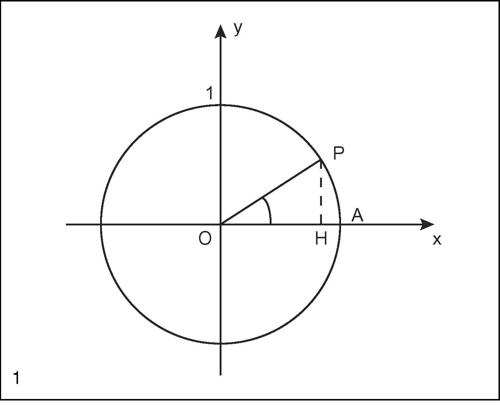
coseno di un angolo acuto α di un qualsiasi triangolo rettangolo, è il rapporto tra il cateto adiacente ad α e l’ipotenusa del triangolo. Per la proprietà di similitudine dei triangoli, tale rapporto è indipendente dal triangolo considerato e dipende solo dall’ampiezza dell’angolo. È indicato con il simbolo cos(α) o anche cosα. Per generalizzare la definizione ad angoli di ampiezza qualunque si considera una circonferenza centrata nell’origine di un riferimento cartesiano e di raggio unitario (detta circonferenza goniometrica). Data un’ampiezza α, si considera quindi l’angolo di tale ampiezza che ha per lati il semiasse positivo delle ascisse e una semiretta uscente dall’origine degli assi, in senso antiorario se α è positivo, orario altrimenti. Il coseno di α è l’ascissa del punto P in cui tale lato (OP) interseca la circonferenza goniometrica; il seno di α è invece la sua ordinata. Vale l’identità fondamentale della trigonometria:

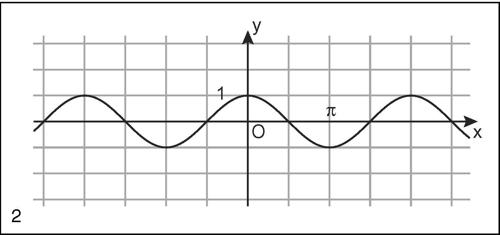
Con tale generalizzazione si definisce la funzione goniometrica di variabile reale y = cos(x), che è definita in tutto R, ha come immagine [−1,1] (perché −1 ≤ cos(x) ≤ 1 per ogni x) ed è periodica di periodo 2π. Per il coseno valgono le seguenti formule:

• cos(α + β) = cosαcosβ − sinαsinβ

(formula di addizione)

• cos(α − β) = cosαcosβ – sinαsinβ

(formula di sottrazione)

• cos(2α) = cos²α − sin²α

(formula di duplicazione)

dove il segno positivo o negativo va dedotto considerando il quadrante in cui cade l’angolo di ampiezza α/2;

La funzione coseno è inoltre sviluppabile in serie di potenze in questo modo: