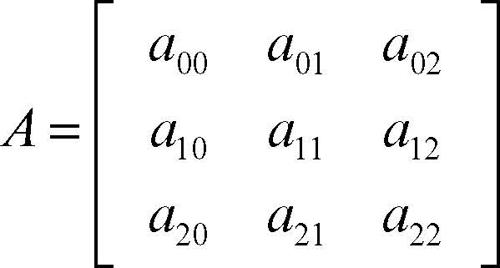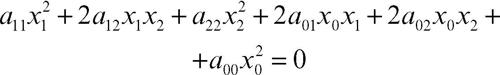conica
conica
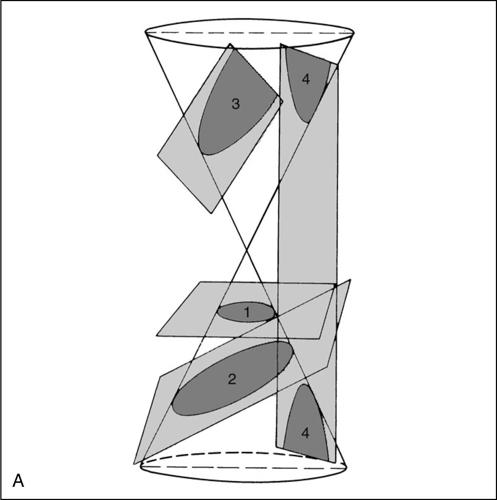
conica curva algebrica piana del secondo ordine ottenuta intersecando una superficie conica circolare indefinita con un piano non passante per il vertice. A seconda della posizione reciproca di cono e piano la curva ottenuta è detta:
• ellisse, se la superficie conica è intersecata da un piano non passante per il vertice del cono e non parallelo ad alcuna generatrice, in modo da incontrarle tutte su una stessa falda del cono (se il piano è perpendicolare all’asse del cono si ha una circonferenza);
• parabola, se la superficie conica è intersecata da un piano non passante per il vertice del cono e parallelo a una sola generatrice, in modo da incontrare tutte le altre su una stessa falda del cono;
• iperbole, se la superficie conica è intersecata da un piano non passante per il vertice del cono e parallelo a due generatrici, in modo da incontrare tutte le altre su entrambe le falde del cono.
Ciascuno dei tre tipi di conica può essere definito come luogo geometrico:
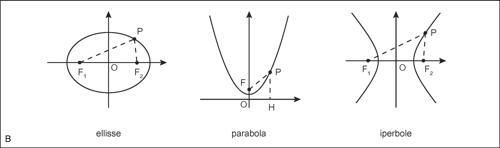
• l’ellisse è il luogo dei punti del piano tali che la somma delle loro distanze da due punti fissi detti fuochi risulti costante (se i fuochi coincidono si ha una circonferenza);
• la parabola è il luogo dei punti del piano equidistanti da un punto fisso detto fuoco e da una retta fissa detta direttrice, non passante per il fuoco;
• l’iperbole è il luogo dei punti del piano tali che la differenza, in valore assoluto, delle loro distanze da due punti fissi detti fuochi risulti costante.
Una ulteriore definizione di conica si ottiene assegnando un punto F detto fuoco, una retta d detta direttrice e un numero reale e ≥ 0 detto eccentricità. La conica è definita come il luogo dei punti del piano P tali che la loro distanza da F sia uguale alla loro distanza da d moltiplicata per e (o, in altri termini, tali che le loro distanze dal fuoco e dalla direttrice stiano in un rapporto costante e). Il valore dell’eccentricità discrimina il tipo di conica:
• se 0 ≤ e < 1 si ha un’ellisse (in particolare una circonferenza se e = 0);
• se e = 1 si ha una parabola;
• se e > 1 si ha un’iperbole.
Si dice asse di una conica una retta rispetto alla quale la conica risulta simmetrica. Ellisse e iperbole hanno due assi di simmetria costituiti dalla retta per i fuochi e dall’asse del segmento che congiunge i fuochi. La parabola ha un solo asse di simmetria dato dalla perpendicolare alla direttrice condotta per il fuoco. I punti di intersezione di una conica con i suoi assi sono detti vertici: nell’ellisse vi sono quattro vertici reali, nell’iperbole due vertici reali e due immaginari, nella parabola un vertice proprio e uno improprio, corrispondente alla direzione del suo asse. Fuochi di una conica sono i punti tali che due rette ortogonali passanti per essi siano coniugati rispetto alla conica; essi non appartengono alla conica essendo interni a essa. Rette tangenti alla conica e passanti per un fuoco sono rette isotrope. L’ellisse e l’iperbole hanno due fuochi reali situati sull’asse maggiore (asse focale) e, rispettivamente, sull’asse trasverso, e inoltre due fuochi immaginari; la parabola ha un fuoco reale situato sull’asse, mentre l’altro fuoco è il punto improprio corrispondente alla direzione dell’asse della parabola. La circonferenza ha due fuochi coincidenti in un unico punto, il suo centro. Direttrici di una conica sono le polari dei fuochi. A ogni fuoco reale corrisponde una direttrice anch’essa reale, esterna alla conica e perpendicolare all’asse focale.
Si dice diametro di una conica ogni retta (o segmento) che congiunge due punti distinti della conica. Il punto di intersezione degli assi di iperbole o ellisse è detto centro della conica. Il centro della conica è centro di simmetria. Ellisse e iperbole sono considerate coniche con centro proprio, mentre la parabola non è considerata una conica a centro in quanto il suo centro è un punto improprio.
Se il piano che interseca la superficie conica passa per il vertice del cono, la sezione ottenuta viene detta conica degenere. Le coniche degeneri possono essere dei seguenti tipi:
• iperbole degenere, costituita da una coppia di rette incidenti. Il piano sezione passa per il vertice e interseca la superficie conica lungo due generatrici;
• parabola degenere, costituita da una coppia di rette coincidenti. Il piano sezione passa per il vertice e risulta tangente a una generatrice;
• ellisse degenere, costituita da un punto. Il piano sezione passa per il vertice e non ha altri punti reali in comune con la superficie conica.
Se il cono degenera in un cilindro e il piano sezione è parallelo all’asse si ha una conica degenere, di tipo parabolico, costituita da una coppia di rette parallele.
Nel piano euclideo, fissato un sistema di riferimento cartesiano ortogonale avente per assi gli assi della conica si hanno, per ellisse e iperbole rispettivamente, le seguenti equazioni canoniche:
(con a e b non nulli). Per la parabola si ha invece l’equazione canonica y 2 = px, avendo scelto come asse delle ascisse l’asse della parabola e come origine il suo vertice. Assumendo come origine di un sistema di coordinate polari un fuoco e come asse polare l’asse focale, l’equazione di una conica è
dove k è una costante, ed e è l’eccentricità.
Più in generale, in un sistema di riferimento cartesiano ortogonale Oxy l’equazione di una conica è:
con a11, a22, a12 non tutti nulli. Ponendo a21 = a12, a10 = a01, a20 = a02 si può considerare la matrice simmetrica a essa associata:
La conica non è degenere se e solo se il determinante di A non è nullo. Se il rango della matrice è 2, la conica è detta semplicemente degenere, se è 1 è detta doppiamente degenere.
Nel piano proiettivo complesso l’equazione di una conica, in coordinate omogenee, si ottiene uguagliando a zero un polinomio omogeneo di secondo grado
Moltiplicando entrambi i membri dell’equazione per un fattore k ≠ 0, si ottiene un’equazione equivalente; quindi i coefficienti essenziali dell’equazione di una conica sono cinque e pertanto le coniche del piano sono ∞5. Ciò vuol dire che una conica è assegnata mediante cinque punti. Se il polinomio a primo membro dell’equazione di una conica è riducibile, è cioè scomponibile nel prodotto di due polinomi di primo grado, la conica è degenere ed è costituita da due rette reali o immaginarie. L’espressione
detta discriminante della conica, ha il seguente significato geometrico:
• se δ > 0, la conica ha due punti distinti sulla retta impropria ed è un’iperbole;
• se δ = 0, la conica è tangente in un punto alla retta impropria ed è una parabola;
• se δ < 0, la conica è priva di punti all’infinito ed è un’ellisse.
Un’iperbole è dotata di due asintoti costituiti dalle rette passanti per il suo centro e aventi la direzione dei suoi punti impropri. Ellisse e parabola sono prive di asintoti.
Per determinare la retta tangente a una conica in un punto P0(x0, y0) si considera il sistema di secondo grado formato dall’equazione della conica e da quella della retta generica passante per tale punto
e si impone che l’equazione risolvente del sistema abbia discriminante nullo. Nel piano euclideo R2, se il punto P0 appartiene alla conica si trova una sola retta tangente, la quale non interseca la conica in nessun altro punto: ciò mostra che la conica “racchiude” una regione convessa; se il punto P0 non appartiene alla conica, si trovano nessuna oppure due rette tangenti, a seconda che il punto sia interno o esterno a tale regione convessa.
Classificazione delle coniche
Le coniche sono classificate in base all’ambiente geometrico in cui ci si pone e quindi in base alla loro appartenenza a classi di equivalenza determinate dalle trasformazioni geometriche ammesse. Nel piano euclideo, se si considerano soltanto i punti reali, sono tra loro equivalenti soltanto le coniche tra loro congruenti; esistono quindi infinite ellissi diverse, infinite parabole diverse, infinite iperboli diverse. Nel piano affine sul campo reale le coniche sono classificate in base ai loro punti impropri. Se tali punti sono due e distinti si ha un’iperbole (e i due punti sono le direzioni degli asintoti), se sono due e coincidenti si ha una parabola (e il punto improprio è la direzione del suo asse), se non ci sono punti impropri si ha un’ellisse. Ciò vuol dire che in un piano affine due parabole o due iperboli o due ellissi sono tra loro equivalenti (perché si corrispondono in una trasformazione affine) e quindi esistono soltanto un’ellisse, una parabola, un’iperbole. Nel piano proiettivo reale, non essendoci distinzione tra elementi propri e impropri, tutte le coniche sono equivalenti, cioè è possibile, date due qualsiasi coniche, trasformare, mediante proiettività, l’una nell’altra: esiste una sola conica. Un ulteriore raffinamento della classificazione è possibile considerando come ambiente numerico un campo algebricamente chiuso, quale per esempio il campo dei numeri complessi.
Cenni storici
Fu il matematico greco Menecmo (sec. iv a.C.), allievo di Eudosso, il primo a studiare le sezioni coniche, che per questo furono chiamate «triadi di Menecmo». Sembra che nel tentativo di risolvere il problema di Delo, o della duplicazione del cubo, Menecmo abbia scoperto le tre coniche secando un cono mediante un piano perpendicolare alla generatrice, ottenendo un’ellisse, una parabola o un’iperbole secondo che l’angolo di apertura del cono fosse acuto, retto o ottuso. Lo studio sistematico delle coniche risale al matematico greco Apollonio di Perge (sec. iii a.C.), che dimostrò che si possono ottenere i tre tipi di sezione a partire da unico cono, variando l’inclinazione del piano che taglia il cono. Ciò rappresentò un passo importante nel processo di unificazione dello studio di tali curve. Le opere di Menecmo e le Coniche di Apollonio rappresentarono una forma primitiva di algebra e di sistemi di coordinate; tradotte dal greco all’arabo nel sec. ix d.C., costituirono le basi storiche delle grandi scoperte di Cartesio, Fermat, Eulero. La teoria delle coniche trova infatti il suo perfezionamento nella geometria analitica, mentre la sistemazione completa e definitiva della materia è legata allo sviluppo della geometria proiettiva.
Le coniche rappresentano un modello geometrico fondamentale per molti fenomeni fisici (traiettoria parabolica di un proiettile, orbita ellittica dei pianeti, grafico iperbolico della legge di proporzionalità inversa ecc.) e il loro studio ha tutt’oggi grande importanza in matematica pura e applicata.