congiunzione
congiunzione
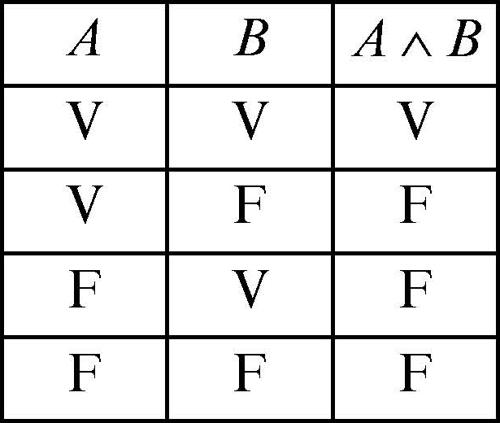
congiunzione connettivo logico che corrisponde, nel linguaggio naturale, alla congiunzione «e», indicato con il simbolo ∧. Dati due enunciati A e B, se ne costruisce un terzo A ∧ B (che si legge «A e B») che è vero solo nel caso in cui siano veri entrambi gli enunciati che lo compongono. Per esempio, se la lettera proposizionale A rappresenta simbolicamente l’enunciato «Marco studia» e la lettera B rappresenta l’enunciato «Marco lavora», allora l’espressione A ∧ B corrisponde all’enunciato «Marco studia e lavora». La tavola di verità della congiunzione evidenzia che A ∧ B è un enunciato vero se entrambi gli enunciati A e B sono veri, è falso negli altri casi:
È possibile unire anche più di due proposizioni attraverso la congiunzione e; per esempio si può connettere la proposizione A ∧ B a un’altra proposizione C formando la proposizione (A ∧ B) ∧ C. Tale proposizione è logicamente equivalente alla proposizione A ∧ (B ∧ C): per la congiunzione vale, quindi, la proprietà associativa (→ equivalenza logica). Per estensione, la congiunzione di un qualsiasi numero di enunciati è un enunciato vero se e solo se tutti gli enunciati che la compongono sono veri. Si definisce congiunzione generalizzata la generalizzazione del connettivo della congiunzione (∧) in modo tale che esso operi su un numero qualunque di enunciati A1, …, An. Essa può essere indicata con il simbolo
ed è vera se e solo se è vera per ogni enunciato che la compone (Ai è vero per ogni i). La precedente scrittura equivale quindi a
Nel modello insiemistico del linguaggio degli enunciati, la congiunzione corrisponde all’intersezione di due insiemi: l’insieme di verità dell’enunciato A e l’insieme di verità dell’enunciato B, dove per insieme di verità di un enunciato si intende l’insieme di quegli elementi per cui l’enunciato è vero. Dati due insiemi A e B, si ha che un elemento appartiene all’intersezione A ∩ B dei due insiemi se e solo se appartiene sia all’insieme A sia all’insieme B.