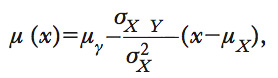condizionamento
condizionamento
Nella teoria della probabilità, procedimento attraverso il quale la probabilità di un evento casuale subisce un aggiornamento in seguito alla conoscenza del verificarsi di un altro evento e prende il nome di probabilità condizionata. Analogamente, il c. di una variabile aleatoria Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X a una o più altre variabili Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X modifica la distribuzione della Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X in seguito all’assunzione di nuove informazioni su Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X. Il risultato del c. è chiamato distribuzione condizionata, che può essere molto diversa da quella originaria o, al contrario, restare la stessa. Nel secondo caso, si parla di indipendenza statistica tra Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X e Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X.
Come esempio di c. si consideri l’esperimento che consiste nel lancio di un dado a 6 facce. La probabilità di ottenere un numero pari è 1/2, trattandosi di un dado in cui ciascuna faccia ha uguale probabilità 1/6 di uscire. Se, però, si suppone che dal lancio del dado uscirà sicuramente una faccia il cui numero è inferiore o uguale a 3, è possibile calcolare la probabilità dell’evento (‘è uscito un numero pari’) condizionatamente all’evento (‘è uscito un numero inferiore a 4’). Questa probabilità è pari a 1/3. Se, invece, si considera il c. dello stesso evento (‘è uscito un numero pari’) all’evento (‘è uscito un numero inferiore o uguale a 4’), in questo caso la probabilità resta uguale a 1/2, in quanto i numeri pari inferiori o uguali a 4 sono esattamente 2 su un totale di 4. Ne consegue che i due eventi sono tra loro indipendenti, poiché il c. di un evento dall’altro non modifica le probabilità.
Distribuzione condizionata
La probabilità di un evento A condizionato a un altro B si ottiene dal rapporto P(A⋃B)/P(B) ed è indicata con P(A/B). Analogamente, se (Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X, Y) è un vettore casuale discreto con funzione probabilità p(y|x, y)=P(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X=y|x,Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X=y|x), la distribuzione di Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X condizionata a Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X è definita dalla funzione p(y|x|y|x)=p(y|x, y|x)/p(y|x), dove p(y|x) è la distribuzione marginale y|x cioè p(y|x)=P(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X=y|x). Se, invece, le variabili Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X e Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X sono continue, la distribuzione di Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X condizionata a Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X è definita dalla funzione di densità condizionata f(y|x|y|x)=f(y|x,y|x)/f(y|x), che si ottiene come rapporto tra la densità congiunta f(y|x,y|x) di Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X e Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X e la densità marginale f(y|x) di Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X. In entrambi i casi, la distribuzione condizionata è definita soltanto per quei valori di y|x per cui il termine a denominatore è strettamente maggiore di zero.
La distribuzione condizionata è una distribuzione di probabilità a tutti gli effetti ed è possibile definirne i momenti. Così la media condizionata e la varianza condizionata sono, per es., rispettivamente la media e la varianza della variabile aleatoria Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X condizionata da Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X=y|x, dove y|x può variare nel supporto della distribuzione di Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X. A ogni diverso valore di y|x, corrisponde una media condizionata E(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X=y|x). Poiché tali medie dipendono dagli eventi Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X=y|x, l’insieme delle medie condizionate descrive una variabile aleatoria, la cui distribuzione di probabilità dipende dalla distribuzione della Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X. In particolare si può calcolare la media di tale variabile aleatoria e si ha E(E(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X))=EY. Tale risultato è noto con il nome di legge delle medie iterate. Un risultato simile, noto come legge della varianza totale, è valido anche per la varianza condizionata: Var(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X)=Var(E(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X)) +E(Var(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X)).
Se la distribuzione di probabilità di una variabile aleatoria Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X rimane invariata nonostante il c. a una variabile Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X, allora le due variabili aleatorie sono tra loro indipendenti. Questo significa che informazioni relative a una delle due variabili non sono utili per acquisire informazioni sull’altra.
Modelli per la funzione di regressione. È uno dei più importanti campi di applicazione del condizionamento. I modelli di regressione (➔ regressione, modelli e stimatori di) non sono altro che modelli per la media condizionata di Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X dati i regressori Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X. Un caso particolarmente rilevante si ha quando la coppia (Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X,Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X) ha una distribuzione gaussiana bivariata di parametri (μ, Σ), dove μ è il vettore delle medie e Σ è la matrice di varianze e covarianze. In tal caso la media condizionata μ(y|x)=E(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X=y|x) è una funzione lineare in y|x,
dove σXY è la covarianza tra Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X e Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X e σ2Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X è la varianza di Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X. Inoltre, Var(Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X)=σ2Y
(1−ρXY)2, dove ρXY è la correlazione tra X e Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X. Cioè, a differenza della media condizionata, la varianza condizionata non dipende da Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X|Y|X.